IMAGIC-500: IMputation benchmark on A Generative Imaginary Country (500k samples)

Missing data imputation in tabular datasets remains a pivotal challenge in data science and machine learning, particularly within socioeconomic research. However, real-world socioeconomic datasets are typically subject to strict data protection protocols, which often prohibit public sharing, even for synthetic derivatives. This severely limits the reproducibility and accessibility of benchmark studies in such settings. Further, there are very few publicly available synthetic datasets. Thus, there is limited availability of benchmarks for systematic evaluation of imputation methods on socioeconomic datasets, whether real or synthetic. In this study, we utilize the World Bank's publicly available synthetic dataset, Synthetic Data for an Imaginary Country, which closely mimics a real World Bank household survey while being fully public, enabling broad access for methodological research. With this as a starting point, we derived the IMAGIC-500 dataset: we select a subset of 500k individuals across approximately 100k households with 19 socioeconomic features, designed to reflect the hierarchical structure of real-world household surveys. This paper introduces a comprehensive missing data imputation benchmark on IMAGIC-500 under various missing mechanisms (MCAR, MAR, MNAR) and missingness ratios (10\%, 20\%, 30\%, 40\%, 50\%). Our evaluation considers the imputation accuracy for continuous and categorical variables, computational efficiency, and impact on downstream predictive tasks, such as estimating educational attainment at the individual level. The results highlight the strengths and weaknesses of statistical, traditional machine learning, and deep learning imputation techniques, including recent diffusion-based methods. The IMAGIC-500 dataset and benchmark aim to facilitate the development of robust imputation algorithms and foster reproducible social science research.

Scalable Spatiotemporal Inference with Biased Scan Attention Transformer Neural Processes

Neural Processes (NPs) are a rapidly evolving class of models designed to directly model the posterior predictive distribution of stochastic processes. While early architectures were developed primarily as a scalable alternative to Gaussian Processes (GPs), modern NPs tackle far more complex and data hungry applications spanning geology, epidemiology, climate, and robotics. These applications have placed increasing pressure on the scalability of these models, with many architectures compromising accuracy for scalability. In this paper, we demonstrate that this tradeoff is often unnecessary, particularly when modeling fully or partially translation invariant processes. We propose a versatile new architecture, the Biased Scan Attention Transformer Neural Process (BSA-TNP), which introduces Kernel Regression Blocks (KRBlocks), group-invariant attention biases, and memory-efficient Biased Scan Attention (BSA). BSA-TNP is able to: (1) match or exceed the accuracy of the best models while often training in a fraction of the time, (2) exhibit translation invariance, enabling learning at multiple resolutions simultaneously, (3) transparently model processes that evolve in both space and time, (4) support high dimensional fixed effects, and (5) scale gracefully -- running inference with over 1M test points with 100K context points in under a minute on a single 24GB GPU.

DeepRV: pre-trained spatial priors for accelerated disease mapping

Recently introduced prior-encoding deep generative models (e.g., PriorVAE, $\pi$VAE, and PriorCVAE) have emerged as powerful tools for scalable Bayesian inference by emulating complex stochastic processes like Gaussian processes (GPs). However, these methods remain largely a proof-of-concept and inaccessible to practitioners. We propose DeepRV, a lightweight, decoder-only approach that accelerates training, and enhances real-world applicability in comparison to current VAE-based prior encoding approaches. Leveraging probabilistic programming frameworks (e.g., NumPyro) for inference, DeepRV achieves significant speedups while also improving the quality of parameter inference, closely matching full MCMC sampling. We showcase its effectiveness in process emulation and spatial analysis of the UK using simulated data, gender-wise cancer mortality rates for individuals under 50, and HIV prevalence in Zimbabwe. To bridge the gap between theory and practice, we provide a user-friendly API, enabling scalable and efficient Bayesian inference.

Indirect Query Bayesian Optimization with Integrated Feedback

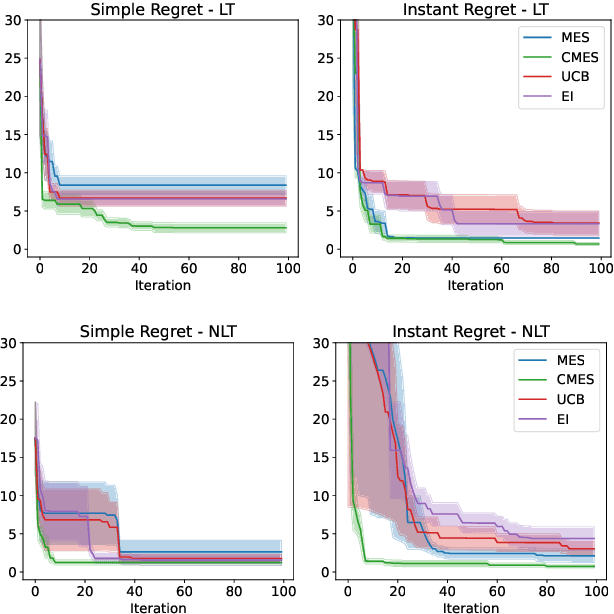
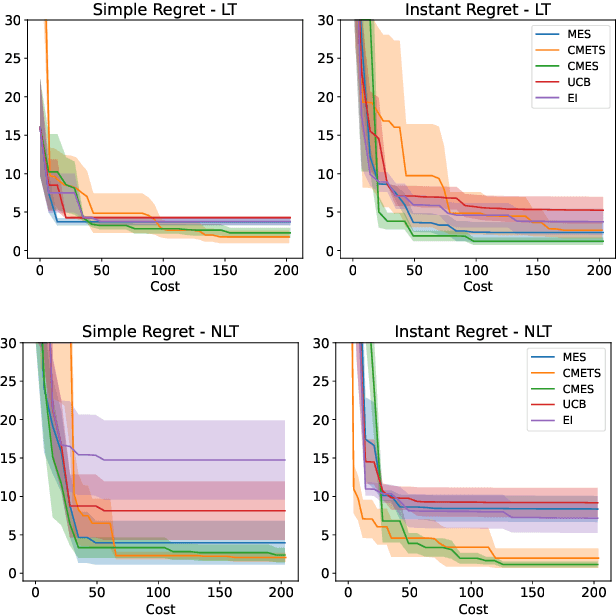
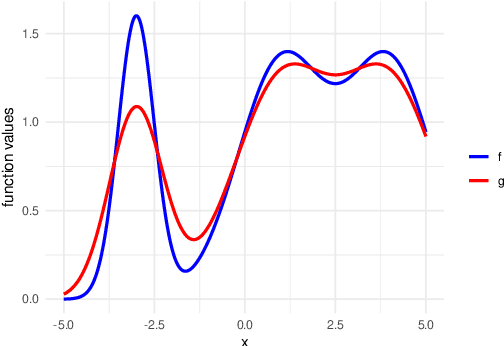
We develop the framework of Indirect Query Bayesian Optimization (IQBO), a new class of Bayesian optimization problems where the integrated feedback is given via a conditional expectation of the unknown function $f$ to be optimized. The underlying conditional distribution can be unknown and learned from data. The goal is to find the global optimum of $f$ by adaptively querying and observing in the space transformed by the conditional distribution. This is motivated by real-world applications where one cannot access direct feedback due to privacy, hardware or computational constraints. We propose the Conditional Max-Value Entropy Search (CMES) acquisition function to address this novel setting, and propose a hierarchical search algorithm to address the multi-resolution setting and improve the computational efficiency. We show regret bounds for our proposed methods and demonstrate the effectiveness of our approaches on simulated optimization tasks.

Uncertainty-Aware Regression for Socio-Economic Estimation via Multi-View Remote Sensing

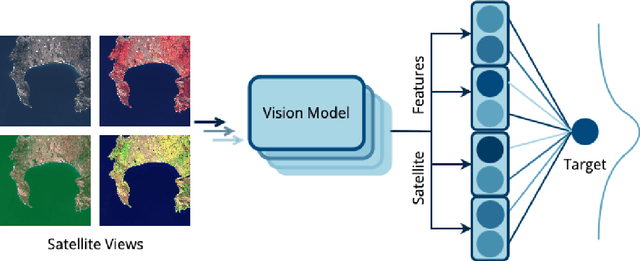
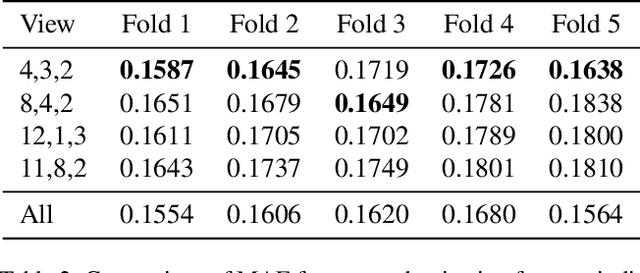
Remote sensing imagery offers rich spectral data across extensive areas for Earth observation. Many attempts have been made to leverage these data with transfer learning to develop scalable alternatives for estimating socio-economic conditions, reducing reliance on expensive survey-collected data. However, much of this research has primarily focused on daytime satellite imagery due to the limitation that most pre-trained models are trained on 3-band RGB images. Consequently, modeling techniques for spectral bands beyond the visible spectrum have not been thoroughly investigated. Additionally, quantifying uncertainty in remote sensing regression has been less explored, yet it is essential for more informed targeting and iterative collection of ground truth survey data. In this paper, we introduce a novel framework that leverages generic foundational vision models to process remote sensing imagery using combinations of three spectral bands to exploit multi-spectral data. We also employ methods such as heteroscedastic regression and Bayesian modeling to generate uncertainty estimates for the predictions. Experimental results demonstrate that our method outperforms existing models that use RGB or multi-spectral models with unstructured band usage. Moreover, our framework helps identify uncertain predictions, guiding future ground truth data acquisition.

Transformer Neural Processes -- Kernel Regression

Stochastic processes model various natural phenomena from disease transmission to stock prices, but simulating and quantifying their uncertainty can be computationally challenging. For example, modeling a Gaussian Process with standard statistical methods incurs an $\mathcal{O}(n^3)$ penalty, and even using state-of-the-art Neural Processes (NPs) incurs an $\mathcal{O}(n^2)$ penalty due to the attention mechanism. We introduce the Transformer Neural Process - Kernel Regression (TNP-KR), a new architecture that incorporates a novel transformer block we call a Kernel Regression Block (KRBlock), which reduces the computational complexity of attention in transformer-based Neural Processes (TNPs) from $\mathcal{O}((n_C+n_T)^2)$ to $O(n_C^2+n_Cn_T)$ by eliminating masked computations, where $n_C$ is the number of context, and $n_T$ is the number of test points, respectively, and a fast attention variant that further reduces all attention calculations to $\mathcal{O}(n_C)$ in space and time complexity. In benchmarks spanning such tasks as meta-regression, Bayesian optimization, and image completion, we demonstrate that the full variant matches the performance of state-of-the-art methods while training faster and scaling two orders of magnitude higher in number of test points, and the fast variant nearly matches that performance while scaling to millions of both test and context points on consumer hardware.

Graph Agnostic Causal Bayesian Optimisation

We study the problem of globally optimising a target variable of an unknown causal graph on which a sequence of soft or hard interventions can be performed. The problem of optimising the target variable associated with a causal graph is formalised as Causal Bayesian Optimisation (CBO). We study the CBO problem under the cumulative regret objective with unknown causal graphs for two settings, namely structural causal models with hard interventions and function networks with soft interventions. We propose Graph Agnostic Causal Bayesian Optimisation (GACBO), an algorithm that actively discovers the causal structure that contributes to achieving optimal rewards. GACBO seeks to balance exploiting the actions that give the best rewards against exploring the causal structures and functions. To the best of our knowledge, our work is the first to study causal Bayesian optimization with cumulative regret objectives in scenarios where the graph is unknown or partially known. We show our proposed algorithm outperforms baselines in simulated experiments and real-world applications.

KidSat: satellite imagery to map childhood poverty dataset and benchmark

Satellite imagery has emerged as an important tool to analyse demographic, health, and development indicators. While various deep learning models have been built for these tasks, each is specific to a particular problem, with few standard benchmarks available. We propose a new dataset pairing satellite imagery and high-quality survey data on child poverty to benchmark satellite feature representations. Our dataset consists of 33,608 images, each 10 km $\times$ 10 km, from 19 countries in Eastern and Southern Africa in the time period 1997-2022. As defined by UNICEF, multidimensional child poverty covers six dimensions and it can be calculated from the face-to-face Demographic and Health Surveys (DHS) Program . As part of the benchmark, we test spatial as well as temporal generalization, by testing on unseen locations, and on data after the training years. Using our dataset we benchmark multiple models, from low-level satellite imagery models such as MOSAIKS , to deep learning foundation models, which include both generic vision models such as Self-Distillation with no Labels (DINOv2) models and specific satellite imagery models such as SatMAE. We provide open source code for building the satellite dataset, obtaining ground truth data from DHS and running various models assessed in our work.

Deep learning and MCMC with aggVAE for shifting administrative boundaries: mapping malaria prevalence in Kenya

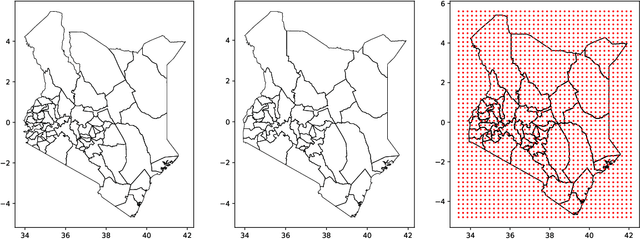
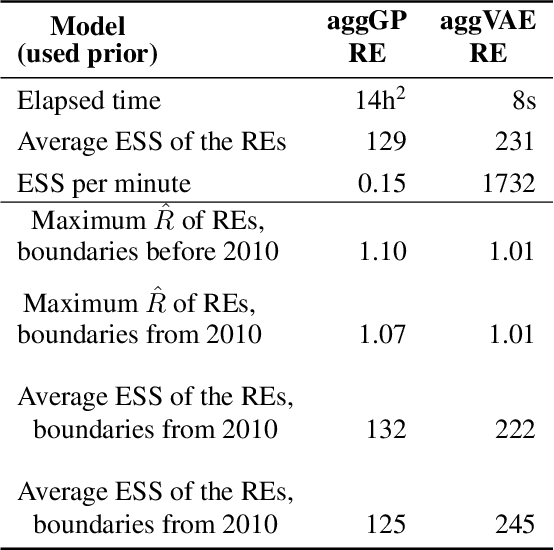
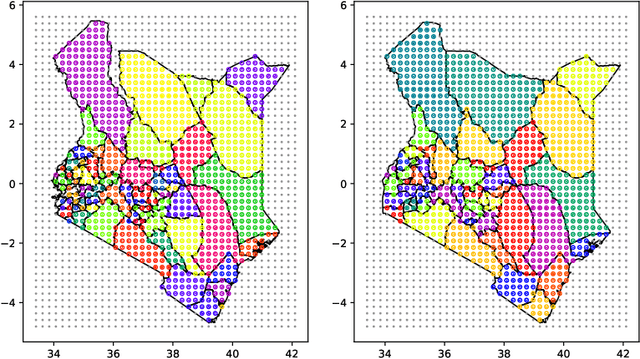
Model-based disease mapping remains a fundamental policy-informing tool in public health and disease surveillance with hierarchical Bayesian models being the current state-of-the-art approach. When working with areal data, e.g. aggregates at the administrative unit level such as district or province, routinely used models rely on the adjacency structure of areal units to account for spatial correlations. The goal of disease surveillance systems is to track disease outcomes over time, but this provides challenging in situations of crises, such as political changes, leading to changes of administrative boundaries. Kenya is an example of such country. Moreover, adjacency-based approach ignores the continuous nature of spatial processes and cannot solve the change-of-support problem, i.e. when administrative boundaries change. We present a novel, practical, and easy to implement solution relying on a methodology combining deep generative modelling and fully Bayesian inference. We build on the recent work of PriorVAE able to encode spatial priors over small areas with variational autoencoders, to map malaria prevalence in Kenya. We solve the change-of-support problem arising from Kenya changing its district boundaries in 2010. We draw realisations of the Gaussian Process (GP) prior over a fine artificial spatial grid representing continuous space and then aggregate these realisations to the level of administrative boundaries. The aggregated values are then encoded using the PriorVAE technique. The trained priors (aggVAE) are then used at the inference stage instead of the GP priors within a Markov chain Monte Carlo (MCMC) scheme. We demonstrate that it is possible to use the flexible and appropriate model for areal data based on aggregation of continuous priors, and that inference is orders of magnitude faster when using aggVAE than combining the original GP priors and the aggregation step.

PriorCVAE: scalable MCMC parameter inference with Bayesian deep generative modelling

In applied fields where the speed of inference and model flexibility are crucial, the use of Bayesian inference for models with a stochastic process as their prior, e.g. Gaussian processes (GPs) is ubiquitous. Recent literature has demonstrated that the computational bottleneck caused by GP priors or their finite realizations can be encoded using deep generative models such as variational autoencoders (VAEs), and the learned generators can then be used instead of the original priors during Markov chain Monte Carlo (MCMC) inference in a drop-in manner. While this approach enables fast and highly efficient inference, it loses information about the stochastic process hyperparameters, and, as a consequence, makes inference over hyperparameters impossible and the learned priors indistinct. We propose to resolve this issue and disentangle the learned priors by conditioning the VAE on stochastic process hyperparameters. This way, the hyperparameters are encoded alongside GP realisations and can be explicitly estimated at the inference stage. We believe that the new method, termed PriorCVAE, will be a useful tool among approximate inference approaches and has the potential to have a large impact on spatial and spatiotemporal inference in crucial real-life applications. Code showcasing PriorCVAE can be found on GitHub: https://github.com/elizavetasemenova/PriorCVAE