Uncertainty-Aware Regression for Socio-Economic Estimation via Multi-View Remote Sensing

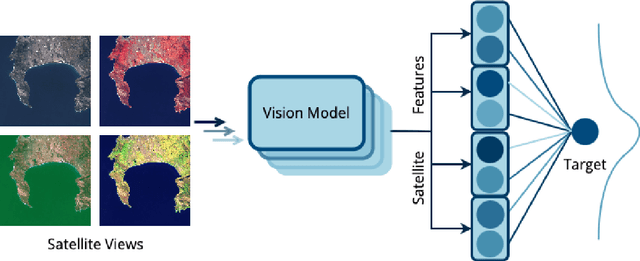
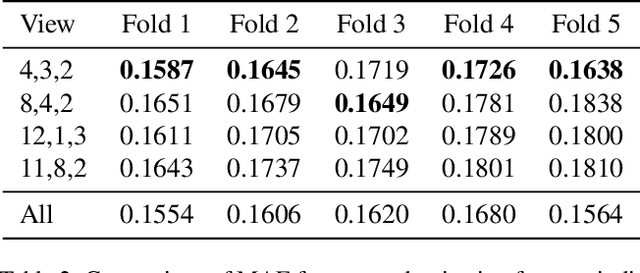
Remote sensing imagery offers rich spectral data across extensive areas for Earth observation. Many attempts have been made to leverage these data with transfer learning to develop scalable alternatives for estimating socio-economic conditions, reducing reliance on expensive survey-collected data. However, much of this research has primarily focused on daytime satellite imagery due to the limitation that most pre-trained models are trained on 3-band RGB images. Consequently, modeling techniques for spectral bands beyond the visible spectrum have not been thoroughly investigated. Additionally, quantifying uncertainty in remote sensing regression has been less explored, yet it is essential for more informed targeting and iterative collection of ground truth survey data. In this paper, we introduce a novel framework that leverages generic foundational vision models to process remote sensing imagery using combinations of three spectral bands to exploit multi-spectral data. We also employ methods such as heteroscedastic regression and Bayesian modeling to generate uncertainty estimates for the predictions. Experimental results demonstrate that our method outperforms existing models that use RGB or multi-spectral models with unstructured band usage. Moreover, our framework helps identify uncertain predictions, guiding future ground truth data acquisition.

Transformer Neural Processes -- Kernel Regression

Stochastic processes model various natural phenomena from disease transmission to stock prices, but simulating and quantifying their uncertainty can be computationally challenging. For example, modeling a Gaussian Process with standard statistical methods incurs an $\mathcal{O}(n^3)$ penalty, and even using state-of-the-art Neural Processes (NPs) incurs an $\mathcal{O}(n^2)$ penalty due to the attention mechanism. We introduce the Transformer Neural Process - Kernel Regression (TNP-KR), a new architecture that incorporates a novel transformer block we call a Kernel Regression Block (KRBlock), which reduces the computational complexity of attention in transformer-based Neural Processes (TNPs) from $\mathcal{O}((n_C+n_T)^2)$ to $O(n_C^2+n_Cn_T)$ by eliminating masked computations, where $n_C$ is the number of context, and $n_T$ is the number of test points, respectively, and a fast attention variant that further reduces all attention calculations to $\mathcal{O}(n_C)$ in space and time complexity. In benchmarks spanning such tasks as meta-regression, Bayesian optimization, and image completion, we demonstrate that the full variant matches the performance of state-of-the-art methods while training faster and scaling two orders of magnitude higher in number of test points, and the fast variant nearly matches that performance while scaling to millions of both test and context points on consumer hardware.