Uncertainty-Aware Regression for Socio-Economic Estimation via Multi-View Remote Sensing

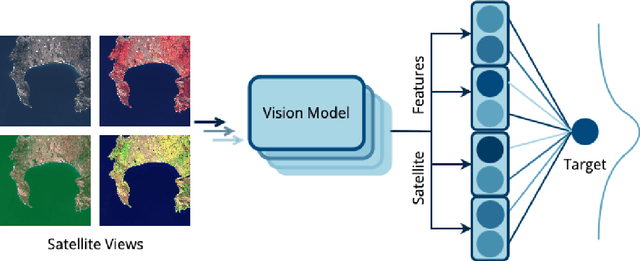
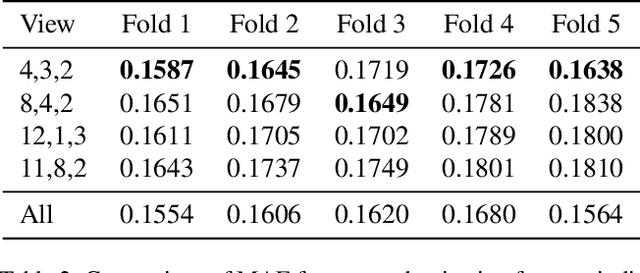
Remote sensing imagery offers rich spectral data across extensive areas for Earth observation. Many attempts have been made to leverage these data with transfer learning to develop scalable alternatives for estimating socio-economic conditions, reducing reliance on expensive survey-collected data. However, much of this research has primarily focused on daytime satellite imagery due to the limitation that most pre-trained models are trained on 3-band RGB images. Consequently, modeling techniques for spectral bands beyond the visible spectrum have not been thoroughly investigated. Additionally, quantifying uncertainty in remote sensing regression has been less explored, yet it is essential for more informed targeting and iterative collection of ground truth survey data. In this paper, we introduce a novel framework that leverages generic foundational vision models to process remote sensing imagery using combinations of three spectral bands to exploit multi-spectral data. We also employ methods such as heteroscedastic regression and Bayesian modeling to generate uncertainty estimates for the predictions. Experimental results demonstrate that our method outperforms existing models that use RGB or multi-spectral models with unstructured band usage. Moreover, our framework helps identify uncertain predictions, guiding future ground truth data acquisition.

Evidential time-to-event prediction model with well-calibrated uncertainty estimation

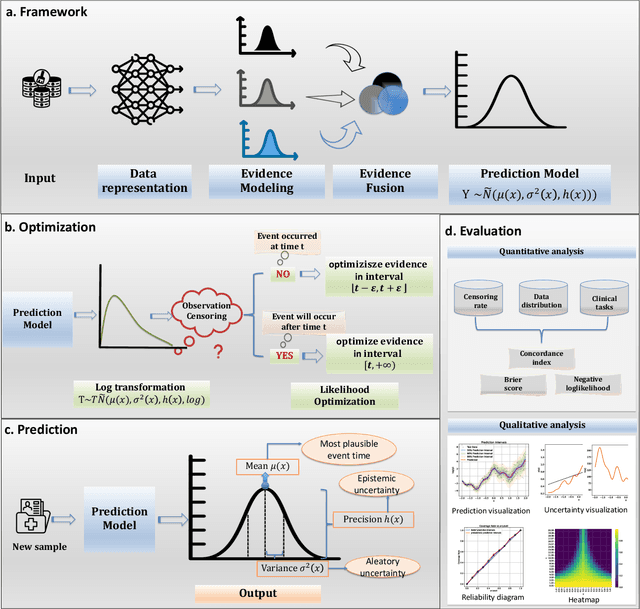
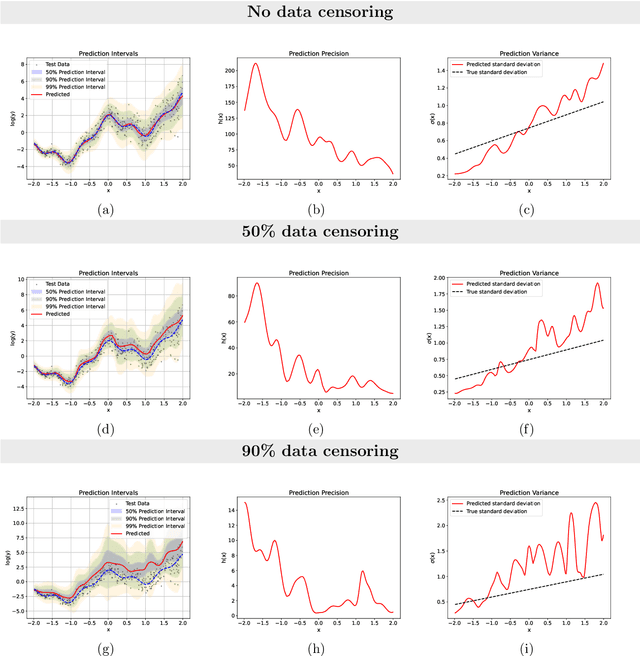
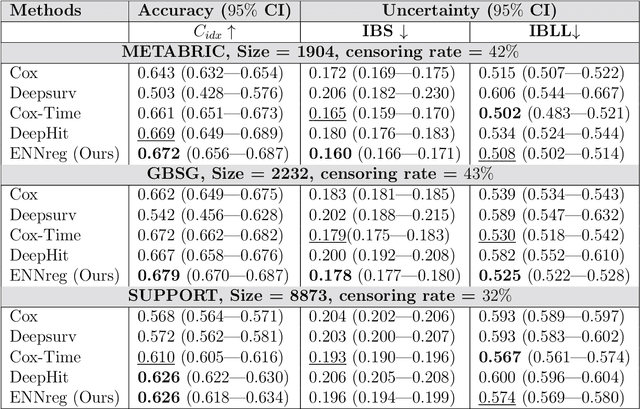
Time-to-event analysis, or Survival analysis, provides valuable insights into clinical prognosis and treatment recommendations. However, this task is typically more challenging than other regression tasks due to the censored observations. Moreover, concerns regarding the reliability of predictions persist among clinicians, mainly attributed to the absence of confidence assessment, robustness, and calibration of prediction. To address those challenges, we introduce an evidential regression model designed especially for time-to-event prediction tasks, with which the most plausible event time, is directly quantified by aggregated Gaussian random fuzzy numbers (GRFNs). The GRFNs are a newly introduced family of random fuzzy subsets of the real line that generalizes both Gaussian random variables and Gaussian possibility distributions. Different from conventional methods that construct models based on strict data distribution, e.g., proportional hazard function, our model only assumes the event time is encoded in a real line GFRN without any strict distribution assumption, therefore offering more flexibility in complex data scenarios. Furthermore, the epistemic and aleatory uncertainty regarding the event time is quantified within the aggregated GRFN as well. Our model can, therefore, provide more detailed clinical decision-making guidance with two more degrees of information. The model is fit by minimizing a generalized negative log-likelihood function that accounts for data censoring based on uncertainty evidence reasoning. Experimental results on simulated datasets with varying data distributions and censoring scenarios, as well as on real-world datasets across diverse clinical settings and tasks, demonstrate that our model achieves both accurate and reliable performance, outperforming state-of-the-art methods.

KidSat: satellite imagery to map childhood poverty dataset and benchmark

Satellite imagery has emerged as an important tool to analyse demographic, health, and development indicators. While various deep learning models have been built for these tasks, each is specific to a particular problem, with few standard benchmarks available. We propose a new dataset pairing satellite imagery and high-quality survey data on child poverty to benchmark satellite feature representations. Our dataset consists of 33,608 images, each 10 km $\times$ 10 km, from 19 countries in Eastern and Southern Africa in the time period 1997-2022. As defined by UNICEF, multidimensional child poverty covers six dimensions and it can be calculated from the face-to-face Demographic and Health Surveys (DHS) Program . As part of the benchmark, we test spatial as well as temporal generalization, by testing on unseen locations, and on data after the training years. Using our dataset we benchmark multiple models, from low-level satellite imagery models such as MOSAIKS , to deep learning foundation models, which include both generic vision models such as Self-Distillation with no Labels (DINOv2) models and specific satellite imagery models such as SatMAE. We provide open source code for building the satellite dataset, obtaining ground truth data from DHS and running various models assessed in our work.

Deep learning and MCMC with aggVAE for shifting administrative boundaries: mapping malaria prevalence in Kenya

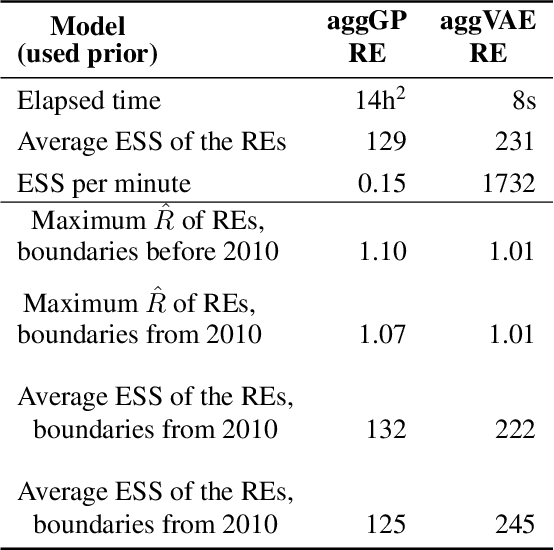
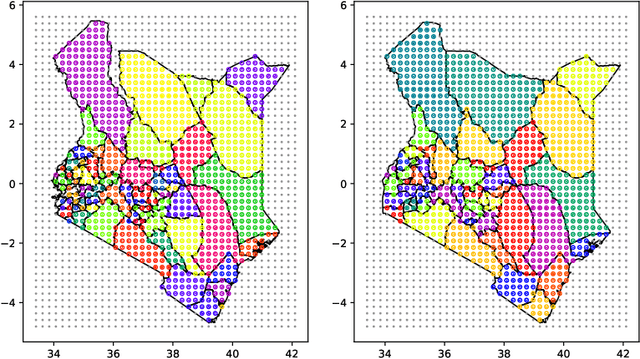
Model-based disease mapping remains a fundamental policy-informing tool in public health and disease surveillance with hierarchical Bayesian models being the current state-of-the-art approach. When working with areal data, e.g. aggregates at the administrative unit level such as district or province, routinely used models rely on the adjacency structure of areal units to account for spatial correlations. The goal of disease surveillance systems is to track disease outcomes over time, but this provides challenging in situations of crises, such as political changes, leading to changes of administrative boundaries. Kenya is an example of such country. Moreover, adjacency-based approach ignores the continuous nature of spatial processes and cannot solve the change-of-support problem, i.e. when administrative boundaries change. We present a novel, practical, and easy to implement solution relying on a methodology combining deep generative modelling and fully Bayesian inference. We build on the recent work of PriorVAE able to encode spatial priors over small areas with variational autoencoders, to map malaria prevalence in Kenya. We solve the change-of-support problem arising from Kenya changing its district boundaries in 2010. We draw realisations of the Gaussian Process (GP) prior over a fine artificial spatial grid representing continuous space and then aggregate these realisations to the level of administrative boundaries. The aggregated values are then encoded using the PriorVAE technique. The trained priors (aggVAE) are then used at the inference stage instead of the GP priors within a Markov chain Monte Carlo (MCMC) scheme. We demonstrate that it is possible to use the flexible and appropriate model for areal data based on aggregation of continuous priors, and that inference is orders of magnitude faster when using aggVAE than combining the original GP priors and the aggregation step.

A comparison of short-term probabilistic forecasts for the incidence of COVID-19 using mechanistic and statistical time series models

Short-term forecasts of infectious disease spread are a critical component in risk evaluation and public health decision making. While different models for short-term forecasting have been developed, open questions about their relative performance remain. Here, we compare short-term probabilistic forecasts of popular mechanistic models based on the renewal equation with forecasts of statistical time series models. Our empirical comparison is based on data of the daily incidence of COVID-19 across six large US states over the first pandemic year. We find that, on average, probabilistic forecasts from statistical time series models are overall at least as accurate as forecasts from mechanistic models. Moreover, statistical time series models better capture volatility. Our findings suggest that domain knowledge, which is integrated into mechanistic models by making assumptions about disease dynamics, does not improve short-term forecasts of disease incidence. We note, however, that forecasting is often only one of many objectives and thus mechanistic models remain important, for example, to model the impact of vaccines or the emergence of new variants.

The interaction of transmission intensity, mortality, and the economy: a retrospective analysis of the COVID-19 pandemic

The COVID-19 pandemic has caused over 6.4 million registered deaths to date, and has had a profound impact on economic activity. Here, we study the interaction of transmission, mortality, and the economy during the SARS-CoV-2 pandemic from January 2020 to December 2022 across 25 European countries. We adopt a Bayesian vector autoregressive model with both fixed and random effects. We find that increases in disease transmission intensity decreases Gross domestic product (GDP) and increases daily excess deaths, with a longer lasting impact on excess deaths in comparison to GDP, which recovers more rapidly. Broadly, our results reinforce the intuitive phenomenon that significant economic activity arises from diverse person-to-person interactions. We report on the effectiveness of non-pharmaceutical interventions (NPIs) on transmission intensity, excess deaths and changes in GDP, and resulting implications for policy makers. Our results highlight a complex cost-benefit trade off from individual NPIs. For example, banning international travel increases GDP however reduces excess deaths. We consider country random effects and their associations with excess changes in GDP and excess deaths. For example, more developed countries in Europe typically had more cautious approaches to the COVID-19 pandemic, prioritising healthcare and excess deaths over economic performance. Long term economic impairments are not fully captured by our model, as well as long term disease effects (Long Covid). Our results highlight that the impact of disease on a country is complex and multifaceted, and simple heuristic conclusions to extract the best outcome from the economy and disease burden are challenging.

Encoding spatiotemporal priors with VAEs for small-area estimation

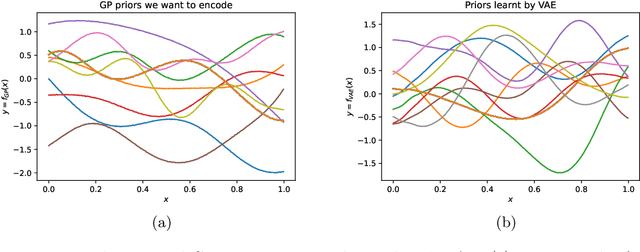
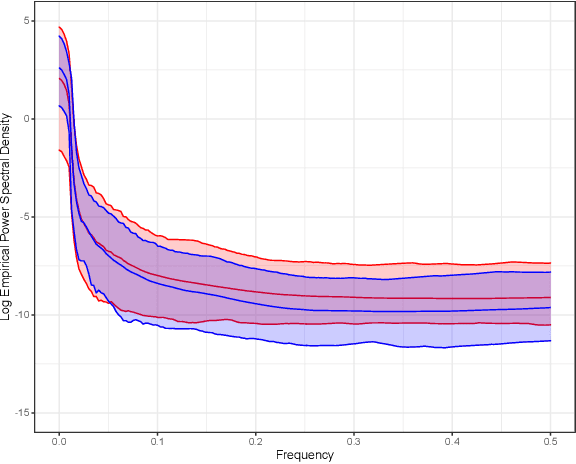
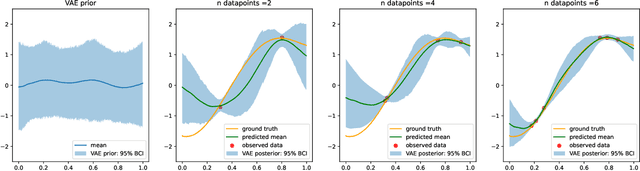
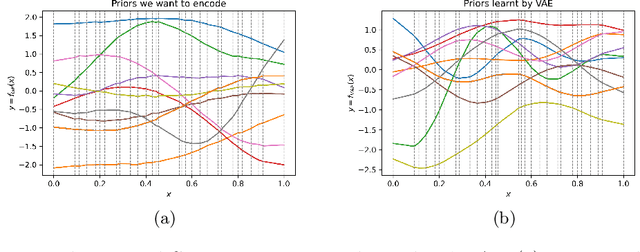
Gaussian processes (GPs), implemented through multivariate Gaussian distributions for a finite collection of data, are the most popular approach in small-area spatiotemporal statistical modelling. In this context they are used to encode correlation structures over space and time and can generalise well in interpolation tasks. Despite their flexibility, off-the-shelf GPs present serious computational challenges which limit their scalability and practical usefulness in applied settings. Here, we propose a novel, deep generative modelling approach to tackle this challenge: for a particular spatiotemporal setting, we approximate a class of GP priors through prior sampling and subsequent fitting of a variational autoencoder (VAE). Given a trained VAE, the resultant decoder allows spatiotemporal inference to become incredibly efficient due to the low dimensional, independently distributed latent Gaussian space representation of the VAE. Once trained, inference using the VAE decoder replaces the GP within a Bayesian sampling framework. This approach provides tractable and easy-to-implement means of approximately encoding spatiotemporal priors and facilitates efficient statistical inference. We demonstrate the utility of our VAE two stage approach on Bayesian, small-area estimation tasks.

Gaussian Process Nowcasting: Application to COVID-19 Mortality Reporting

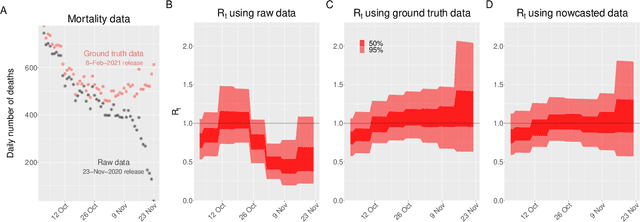
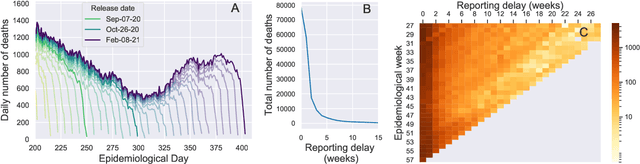
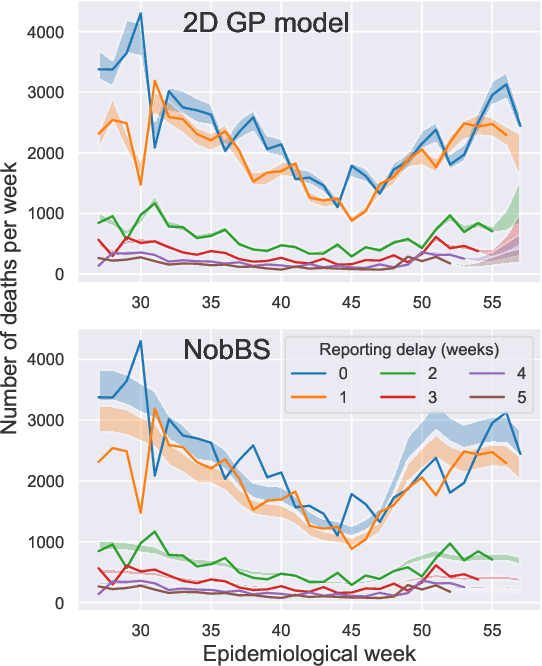
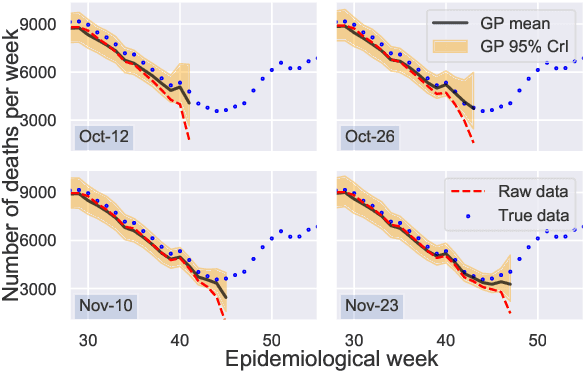
Updating observations of a signal due to the delays in the measurement process is a common problem in signal processing, with prominent examples in a wide range of fields. An important example of this problem is the nowcasting of COVID-19 mortality: given a stream of reported counts of daily deaths, can we correct for the delays in reporting to paint an accurate picture of the present, with uncertainty? Without this correction, raw data will often mislead by suggesting an improving situation. We present a flexible approach using a latent Gaussian process that is capable of describing the changing auto-correlation structure present in the reporting time-delay surface. This approach also yields robust estimates of uncertainty for the estimated nowcasted numbers of deaths. We test assumptions in model specification such as the choice of kernel or hyper priors, and evaluate model performance on a challenging real dataset from Brazil. Our experiments show that Gaussian process nowcasting performs favourably against both comparable methods, and a small sample of expert human predictions. Our approach has substantial practical utility in disease modelling -- by applying our approach to COVID-19 mortality data from Brazil, where reporting delays are large, we can make informative predictions on important epidemiological quantities such as the current effective reproduction number.

Simulating normalising constants with referenced thermodynamic integration: application to COVID-19 model selection

Model selection is a fundamental part of Bayesian statistical inference; a widely used tool in the field of epidemiology. Simple methods such as Akaike Information Criterion are commonly used but they do not incorporate the uncertainty of the model's parameters, which can give misleading choices when comparing models with similar fit to the data. One approach to model selection in a more rigorous way that uses the full posterior distributions of the models is to compute the ratio of the normalising constants (or model evidence), known as Bayes factors. These normalising constants integrate the posterior distribution over all parameters and balance over and under fitting. However, normalising constants often come in the form of intractable, high-dimensional integrals, therefore special probabilistic techniques need to be applied to correctly estimate the Bayes factors. One such method is thermodynamic integration (TI), which can be used to estimate the ratio of two models' evidence by integrating over a continuous path between the two un-normalised densities. In this paper we introduce a variation of the TI method, here referred to as referenced TI, which computes a single model's evidence in an efficient way by using a reference density such as a multivariate normal - where the normalising constant is known. We show that referenced TI, an asymptotically exact Monte Carlo method of calculating the normalising constant of a single model, in practice converges to the correct result much faster than other competing approaches such as the method of power posteriors. We illustrate the implementation of the algorithm on informative 1- and 2-dimensional examples, and apply it to a popular linear regression problem, and use it to select parameters for a model of the COVID-19 epidemic in South Korea.

A unified machine learning approach to time series forecasting applied to demand at emergency departments

There were 25.6 million attendances at Emergency Departments (EDs) in England in 2019 corresponding to an increase of 12 million attendances over the past ten years. The steadily rising demand at EDs creates a constant challenge to provide adequate quality of care while maintaining standards and productivity. Managing hospital demand effectively requires an adequate knowledge of the future rate of admission. Using 8 years of electronic admissions data from two major acute care hospitals in London, we develop a novel ensemble methodology that combines the outcomes of the best performing time series and machine learning approaches in order to make highly accurate forecasts of demand, 1, 3 and 7 days in the future. Both hospitals face an average daily demand of 208 and 106 attendances respectively and experience considerable volatility around this mean. However, our approach is able to predict attendances at these emergency departments one day in advance up to a mean absolute error of +/- 14 and +/- 10 patients corresponding to a mean absolute percentage error of 6.8% and 8.6% respectively. Our analysis compares machine learning algorithms to more traditional linear models. We find that linear models often outperform machine learning methods and that the quality of our predictions for any of the forecasting horizons of 1, 3 or 7 days are comparable as measured in MAE. In addition to comparing and combining state-of-the-art forecasting methods to predict hospital demand, we consider two different hyperparameter tuning methods, enabling a faster deployment of our models without compromising performance. We believe our framework can readily be used to forecast a wide range of policy relevant indicators.