Gaussian Process Nowcasting: Application to COVID-19 Mortality Reporting

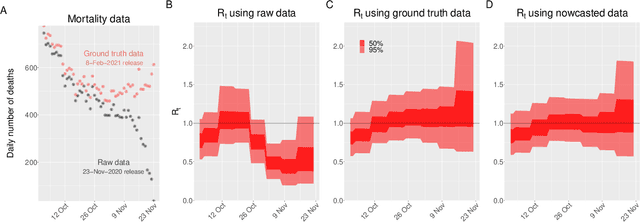
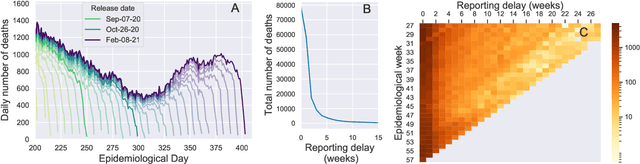
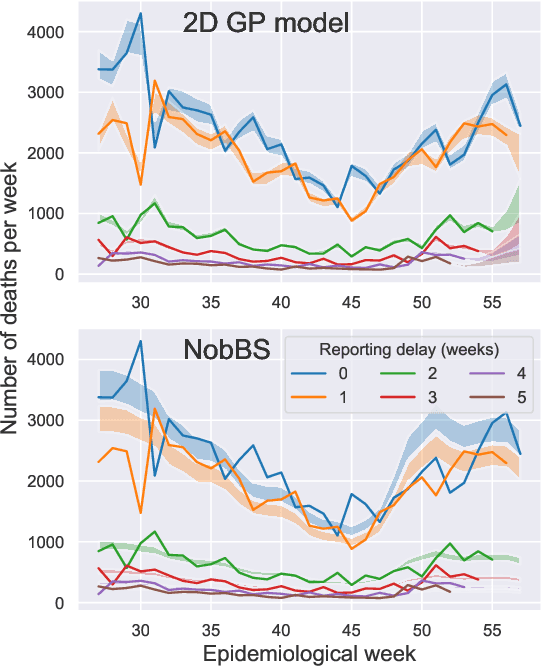
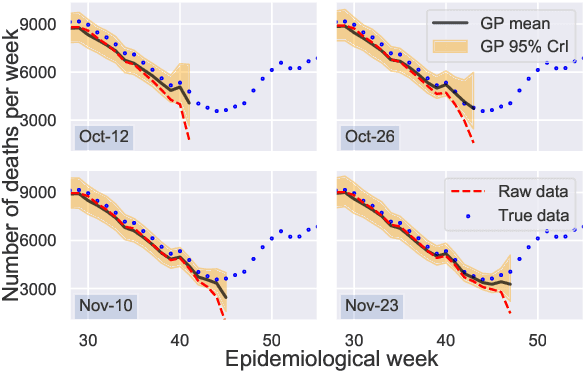
Updating observations of a signal due to the delays in the measurement process is a common problem in signal processing, with prominent examples in a wide range of fields. An important example of this problem is the nowcasting of COVID-19 mortality: given a stream of reported counts of daily deaths, can we correct for the delays in reporting to paint an accurate picture of the present, with uncertainty? Without this correction, raw data will often mislead by suggesting an improving situation. We present a flexible approach using a latent Gaussian process that is capable of describing the changing auto-correlation structure present in the reporting time-delay surface. This approach also yields robust estimates of uncertainty for the estimated nowcasted numbers of deaths. We test assumptions in model specification such as the choice of kernel or hyper priors, and evaluate model performance on a challenging real dataset from Brazil. Our experiments show that Gaussian process nowcasting performs favourably against both comparable methods, and a small sample of expert human predictions. Our approach has substantial practical utility in disease modelling -- by applying our approach to COVID-19 mortality data from Brazil, where reporting delays are large, we can make informative predictions on important epidemiological quantities such as the current effective reproduction number.

Relaxed-Responsibility Hierarchical Discrete VAEs

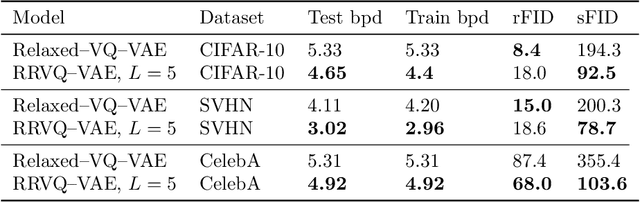
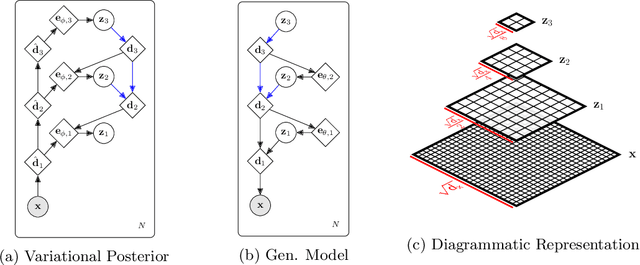
Successfully training Variational Autoencoders (VAEs) with a hierarchy of discrete latent variables remains an area of active research. Leveraging insights from classical methods of inference we introduce $\textit{Relaxed-Responsibility Vector-Quantisation}$, a novel way to parameterise discrete latent variables, a refinement of relaxed Vector-Quantisation. This enables a novel approach to hierarchical discrete variational autoencoder with numerous layers of latent variables that we train end-to-end. Unlike discrete VAEs with a single layer of latent variables, we can produce realistic-looking samples by ancestral sampling: it is not essential to train a second generative model over the learnt latent representations to then sample from and then decode. Further, we observe different layers of our model become associated with different aspects of the data.

A unified construction for series representations and finite approximations of completely random measures

Infinite-activity completely random measures (CRMs) have become important building blocks of complex Bayesian nonparametric models. They have been successfully used in various applications such as clustering, density estimation, latent feature models, survival analysis or network science. Popular infinite-activity CRMs include the (generalized) gamma process and the (stable) beta process. However, except in some specific cases, exact simulation or scalable inference with these models is challenging and finite-dimensional approximations are often considered. In this work, we propose a general and unified framework to derive both series representations and finite-dimensional approximations of CRMs. Our framework can be seen as an extension of constructions based on size-biased sampling of Poisson point process [Perman1992]. It includes as special cases several known series representations as well as novel ones. In particular, we show that one can get novel series representations for the generalized gamma process and the stable beta process. We also provide some analysis of the truncation error.

Modelling sparsity, heterogeneity, reciprocity and community structure in temporal interaction data

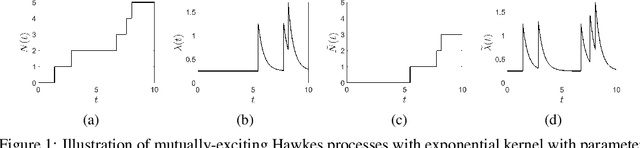
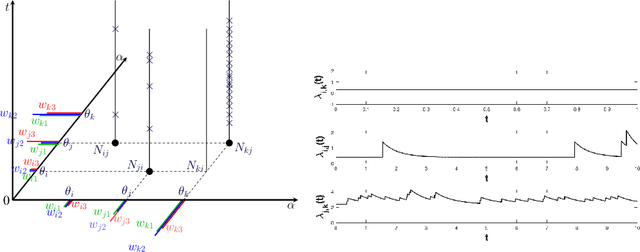
We propose a novel class of network models for temporal dyadic interaction data. Our goal is to capture a number of important features often observed in social interactions: sparsity, degree heterogeneity, community structure and reciprocity. We propose a family of models based on self-exciting Hawkes point processes in which events depend on the history of the process. The key component is the conditional intensity function of the Hawkes Process, which captures the fact that interactions may arise as a response to past interactions (reciprocity), or due to shared interests between individuals (community structure). In order to capture the sparsity and degree heterogeneity, the base (non time dependent) part of the intensity function builds on compound random measures following Todeschini et al. (2016). We conduct experiments on a variety of real-world temporal interaction data and show that the proposed model outperforms many competing approaches for link prediction, and leads to interpretable parameters.

Exchangeable Random Measures for Sparse and Modular Graphs with Overlapping Communities

We propose a novel statistical model for sparse networks with overlapping community structure. The model is based on representing the graph as an exchangeable point process, and naturally generalizes existing probabilistic models with overlapping block-structure to the sparse regime. Our construction builds on vectors of completely random measures, and has interpretable parameters, each node being assigned a vector representing its level of affiliation to some latent communities. We develop methods for simulating this class of random graphs, as well as to perform posterior inference. We show that the proposed approach can recover interpretable structure from two real-world networks and can handle graphs with thousands of nodes and tens of thousands of edges.