A Multi-Resolution Framework for U-Nets with Applications to Hierarchical VAEs

U-Net architectures are ubiquitous in state-of-the-art deep learning, however their regularisation properties and relationship to wavelets are understudied. In this paper, we formulate a multi-resolution framework which identifies U-Nets as finite-dimensional truncations of models on an infinite-dimensional function space. We provide theoretical results which prove that average pooling corresponds to projection within the space of square-integrable functions and show that U-Nets with average pooling implicitly learn a Haar wavelet basis representation of the data. We then leverage our framework to identify state-of-the-art hierarchical VAEs (HVAEs), which have a U-Net architecture, as a type of two-step forward Euler discretisation of multi-resolution diffusion processes which flow from a point mass, introducing sampling instabilities. We also demonstrate that HVAEs learn a representation of time which allows for improved parameter efficiency through weight-sharing. We use this observation to achieve state-of-the-art HVAE performance with half the number of parameters of existing models, exploiting the properties of our continuous-time formulation.

Variational Autoencoders: A Harmonic Perspective

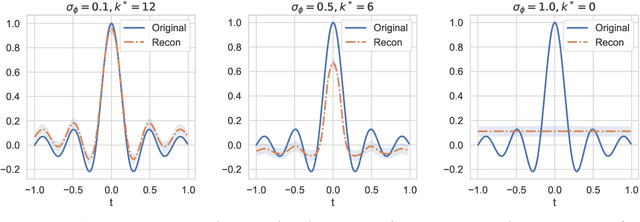
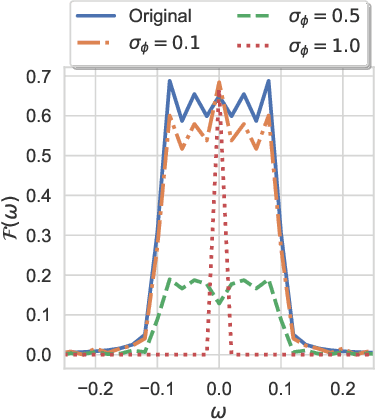
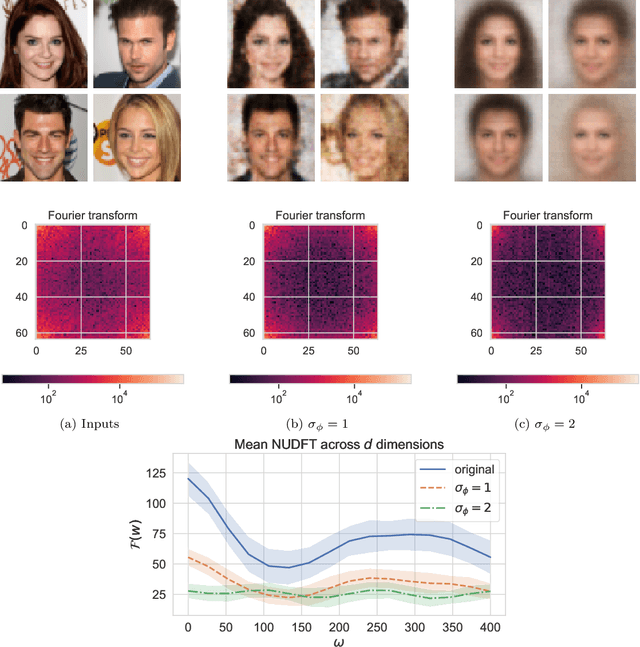
In this work we study Variational Autoencoders (VAEs) from the perspective of harmonic analysis. By viewing a VAE's latent space as a Gaussian Space, a variety of measure space, we derive a series of results that show that the encoder variance of a VAE controls the frequency content of the functions parameterised by the VAE encoder and decoder neural networks. In particular we demonstrate that larger encoder variances reduce the high frequency content of these functions. Our analysis allows us to show that increasing this variance effectively induces a soft Lipschitz constraint on the decoder network of a VAE, which is a core contributor to the adversarial robustness of VAEs. We further demonstrate that adding Gaussian noise to the input of a VAE allows us to more finely control the frequency content and the Lipschitz constant of the VAE encoder networks. To support our theoretical analysis we run experiments with VAEs with small fully-connected neural networks and with larger convolutional networks, demonstrating empirically that our theory holds for a variety of neural network architectures.

Multi-Facet Clustering Variational Autoencoders

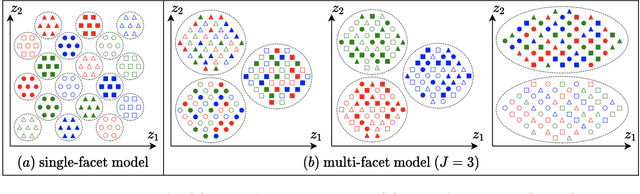
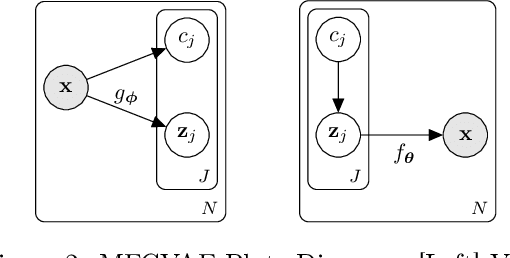
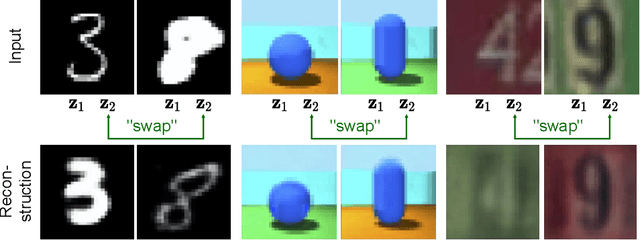
Work in deep clustering focuses on finding a single partition of data. However, high-dimensional data, such as images, typically feature multiple interesting characteristics one could cluster over. For example, images of objects against a background could be clustered over the shape of the object and separately by the colour of the background. In this paper, we introduce Multi-Facet Clustering Variational Autoencoders (MFCVAE), a novel class of variational autoencoders with a hierarchy of latent variables, each with a Mixture-of-Gaussians prior, that learns multiple clusterings simultaneously, and is trained fully unsupervised and end-to-end. MFCVAE uses a progressively-trained ladder architecture which leads to highly stable performance. We provide novel theoretical results for optimising the ELBO analytically with respect to the categorical variational posterior distribution, and corrects earlier influential theoretical work. On image benchmarks, we demonstrate that our approach separates out and clusters over different aspects of the data in a disentangled manner. We also show other advantages of our model: the compositionality of its latent space and that it provides controlled generation of samples.

I Don't Need $\mathbf{u}$: Identifiable Non-Linear ICA Without Side Information

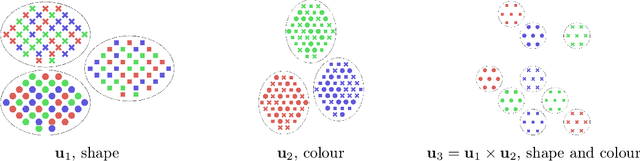
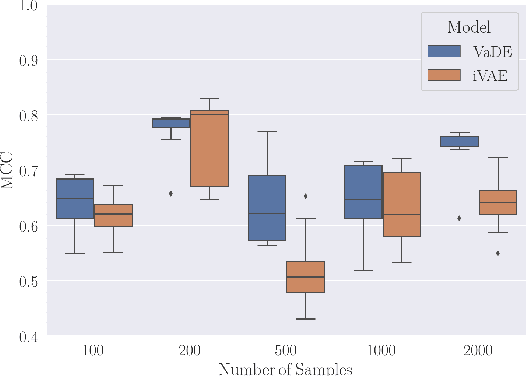
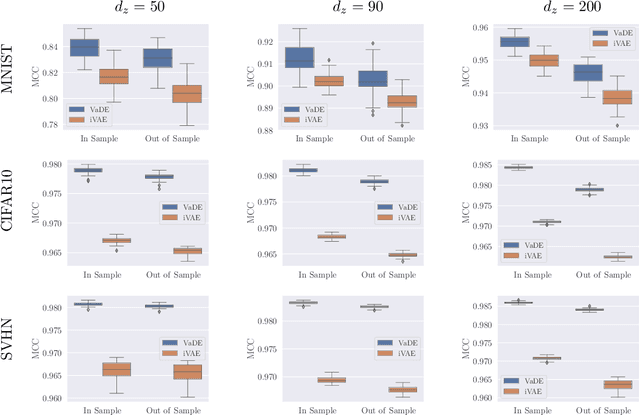
In this work we introduce a new approach for identifiable non-linear ICA models. Recently there has been a renaissance in identifiability results in deep generative models, not least for non-linear ICA. These prior works, however, have assumed access to a sufficiently-informative auxiliary set of observations, denoted $\mathbf{u}$. We show here how identifiability can be obtained in the absence of this side-information, rendering possible fully-unsupervised identifiable non-linear ICA. While previous theoretical results have established the impossibility of identifiable non-linear ICA in the presence of infinitely-flexible universal function approximators, here we rely on the intrinsically-finite modelling capacity of any particular chosen parameterisation of a deep generative model. In particular, we focus on generative models which perform clustering in their latent space -- a model structure which matches previous identifiable models, but with the learnt clustering providing a synthetic form of auxiliary information. We evaluate our proposals using VAEs, on synthetic and image datasets, and find that the learned clusterings function effectively: deep generative models with latent clusterings are empirically identifiable, to the same degree as models which rely on side information.

Certifiably Robust Variational Autoencoders

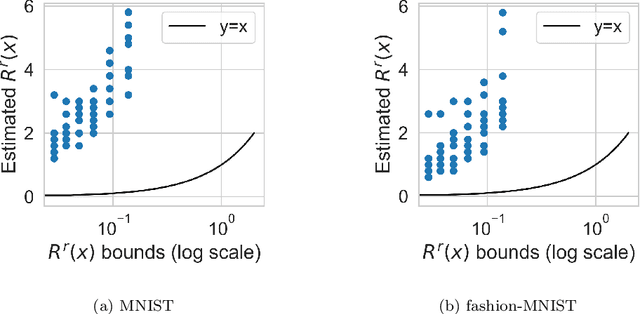
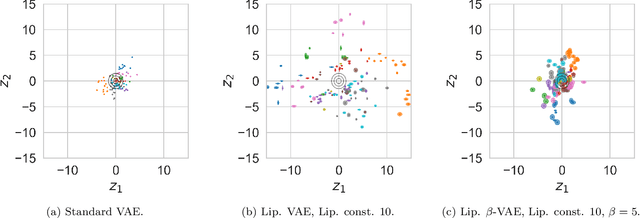
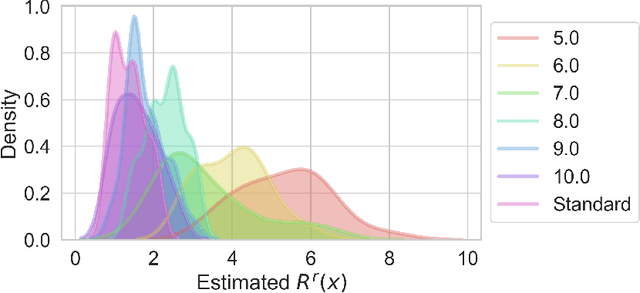
We introduce an approach for training Variational Autoencoders (VAEs) that are certifiably robust to adversarial attack. Specifically, we first derive actionable bounds on the minimal size of an input perturbation required to change a VAE's reconstruction by more than an allowed amount, with these bounds depending on certain key parameters such as the Lipschitz constants of the encoder and decoder. We then show how these parameters can be controlled, thereby providing a mechanism to ensure a priori that a VAE will attain a desired level of robustness. Moreover, we extend this to a complete practical approach for training such VAEs to ensure our criteria are met. Critically, our method allows one to specify a desired level of robustness upfront and then train a VAE that is guaranteed to achieve this robustness. We further demonstrate that these Lipschitz--constrained VAEs are more robust to attack than standard VAEs in practice.

Explicit Regularisation in Gaussian Noise Injections

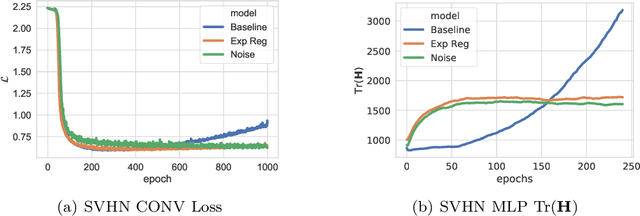
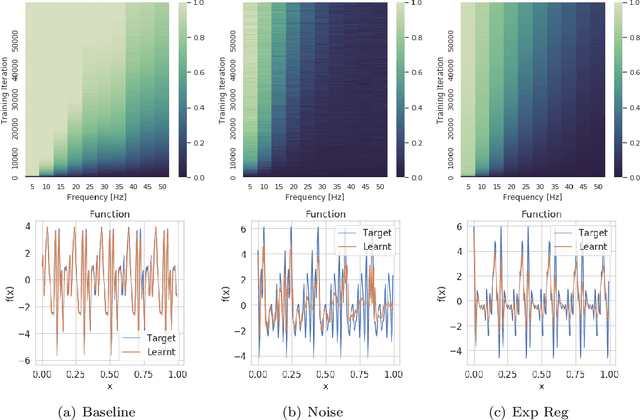
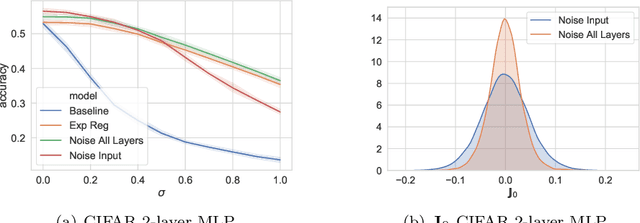
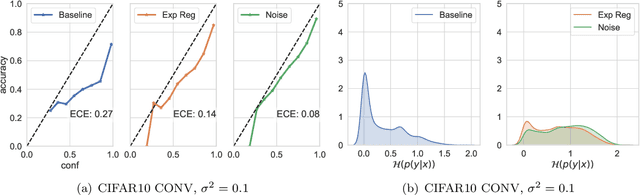
We study the regularisation induced in neural networks by Gaussian noise injections (GNIs). Though such injections have been extensively studied when applied to data, there have been few studies on understanding the regularising effect they induce when applied to network activations. Here we derive the explicit regulariser of GNIs, obtained by marginalising out the injected noise, and show that it is a form of Tikhonov regularisation which penalises functions with high-frequency components in the Fourier domain. We show analytically and empirically that such regularisation produces calibrated classifiers with large classification margins and that the explicit regulariser we derive is able to reproduce these effects.

Towards a Theoretical Understanding of the Robustness of Variational Autoencoders

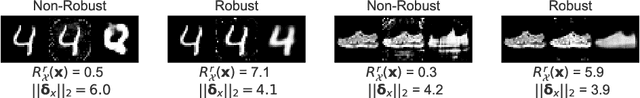
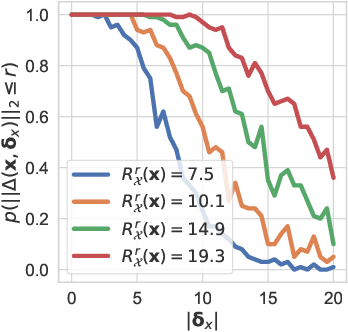
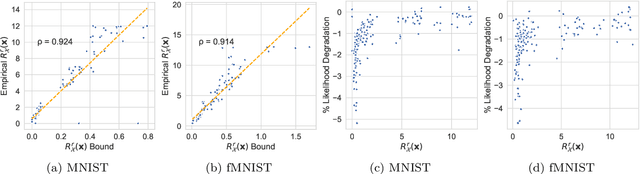
We make inroads into understanding the robustness of Variational Autoencoders (VAEs) to adversarial attacks and other input perturbations. While previous work has developed algorithmic approaches to attacking and defending VAEs, there remains a lack of formalization for what it means for a VAE to be robust. To address this, we develop a novel criterion for robustness in probabilistic models: $r$-robustness. We then use this to construct the first theoretical results for the robustness of VAEs, deriving margins in the input space for which we can provide guarantees about the resulting reconstruction. Informally, we are able to define a region within which any perturbation will produce a reconstruction that is similar to the original reconstruction. To support our analysis, we show that VAEs trained using disentangling methods not only score well under our robustness metrics, but that the reasons for this can be interpreted through our theoretical results.

Relaxed-Responsibility Hierarchical Discrete VAEs

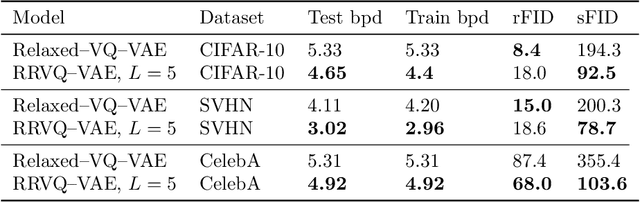
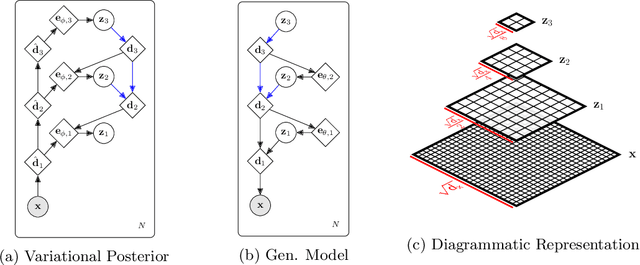
Successfully training Variational Autoencoders (VAEs) with a hierarchy of discrete latent variables remains an area of active research. Leveraging insights from classical methods of inference we introduce $\textit{Relaxed-Responsibility Vector-Quantisation}$, a novel way to parameterise discrete latent variables, a refinement of relaxed Vector-Quantisation. This enables a novel approach to hierarchical discrete variational autoencoder with numerous layers of latent variables that we train end-to-end. Unlike discrete VAEs with a single layer of latent variables, we can produce realistic-looking samples by ancestral sampling: it is not essential to train a second generative model over the learnt latent representations to then sample from and then decode. Further, we observe different layers of our model become associated with different aspects of the data.

Learning Bijective Feature Maps for Linear ICA

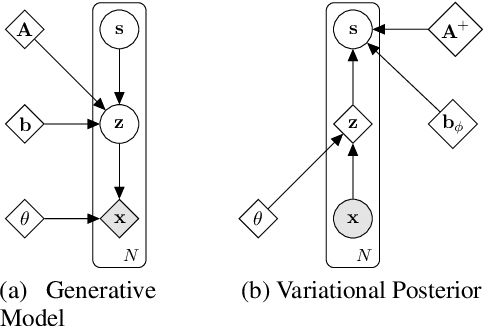
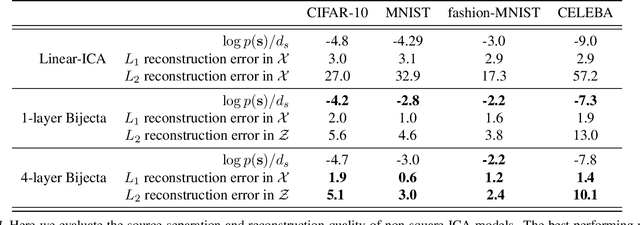
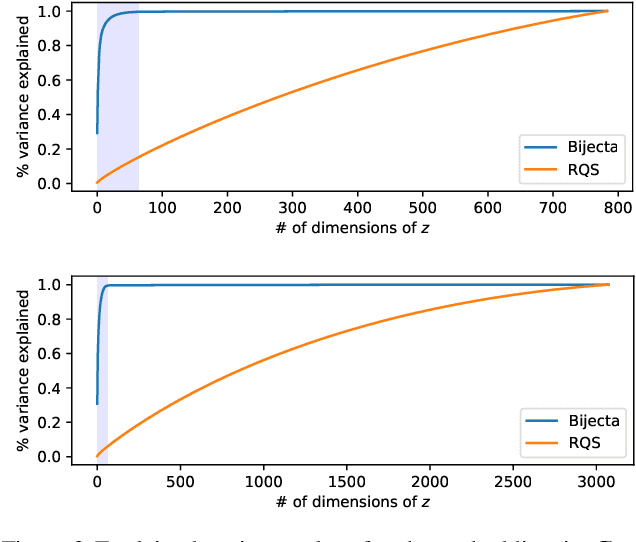
Separating high-dimensional data like images into independent latent factors remains an open research problem. Here we develop a method that jointly learns a linear independent component analysis (ICA) model with non-linear bijective feature maps. By combining these two methods, ICA can learn interpretable latent structure for images. For non-square ICA, where we assume the number of sources is less than the dimensionality of data, we achieve better unsupervised latent factor discovery than flow-based models and linear ICA. This performance scales to large image datasets such as CelebA.

Non-Determinism in TensorFlow ResNets

We show that the stochasticity in training ResNets for image classification on GPUs in TensorFlow is dominated by the non-determinism from GPUs, rather than by the initialisation of the weights and biases of the network or by the sequence of minibatches given. The standard deviation of test set accuracy is 0.02 with fixed seeds, compared to 0.027 with different seeds---nearly 74\% of the standard deviation of a ResNet model is non-deterministic. For test set loss the ratio of standard deviations is more than 80\%. These results call for more robust evaluation strategies of deep learning models, as a significant amount of the variation in results across runs can arise simply from GPU randomness.