Verifiable evaluations of machine learning models using zkSNARKs

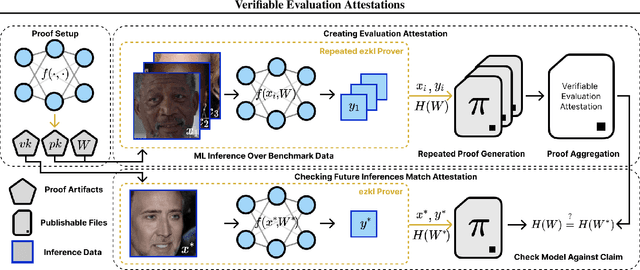
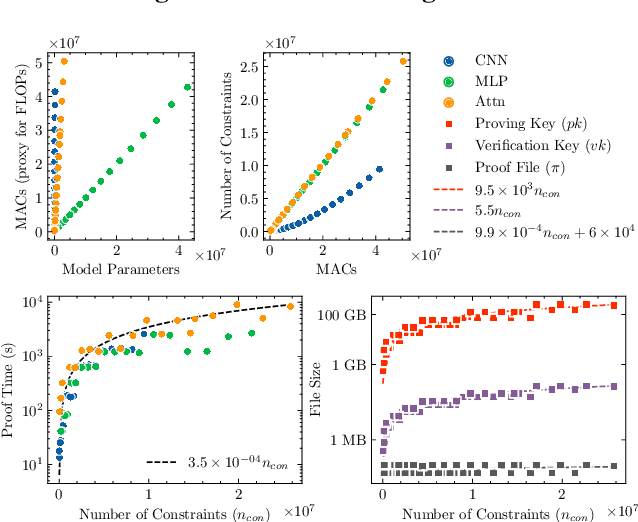
In a world of increasing closed-source commercial machine learning models, model evaluations from developers must be taken at face value. These benchmark results, whether over task accuracy, bias evaluations, or safety checks, are traditionally impossible to verify by a model end-user without the costly or impossible process of re-performing the benchmark on black-box model outputs. This work presents a method of verifiable model evaluation using model inference through zkSNARKs. The resulting zero-knowledge computational proofs of model outputs over datasets can be packaged into verifiable evaluation attestations showing that models with fixed private weights achieve stated performance or fairness metrics over public inputs. These verifiable attestations can be performed on any standard neural network model with varying compute requirements. For the first time, we demonstrate this across a sample of real-world models and highlight key challenges and design solutions. This presents a new transparency paradigm in the verifiable evaluation of private models.

Variational Autoencoders: A Harmonic Perspective

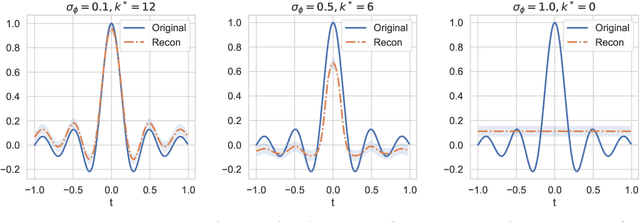
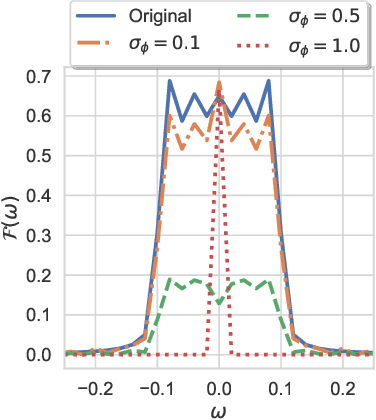
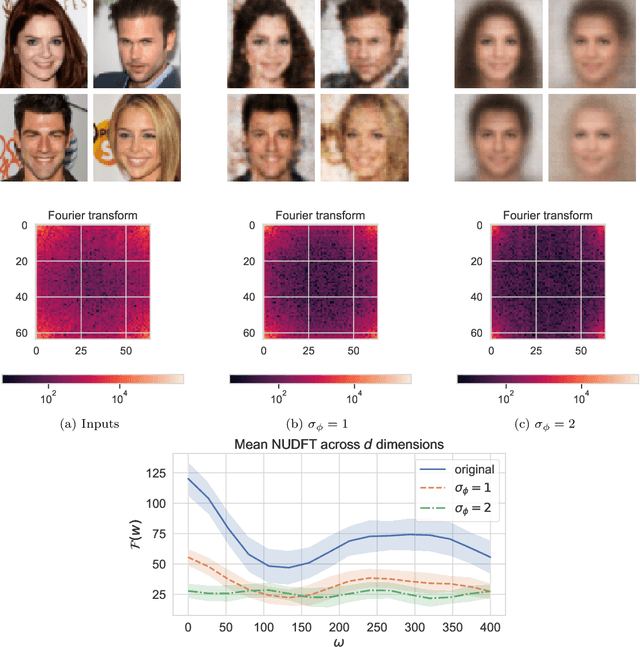
In this work we study Variational Autoencoders (VAEs) from the perspective of harmonic analysis. By viewing a VAE's latent space as a Gaussian Space, a variety of measure space, we derive a series of results that show that the encoder variance of a VAE controls the frequency content of the functions parameterised by the VAE encoder and decoder neural networks. In particular we demonstrate that larger encoder variances reduce the high frequency content of these functions. Our analysis allows us to show that increasing this variance effectively induces a soft Lipschitz constraint on the decoder network of a VAE, which is a core contributor to the adversarial robustness of VAEs. We further demonstrate that adding Gaussian noise to the input of a VAE allows us to more finely control the frequency content and the Lipschitz constant of the VAE encoder networks. To support our theoretical analysis we run experiments with VAEs with small fully-connected neural networks and with larger convolutional networks, demonstrating empirically that our theory holds for a variety of neural network architectures.

Fractal Structure and Generalization Properties of Stochastic Optimization Algorithms

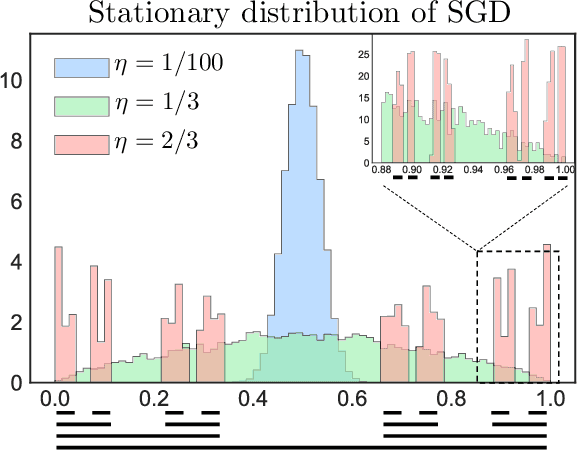
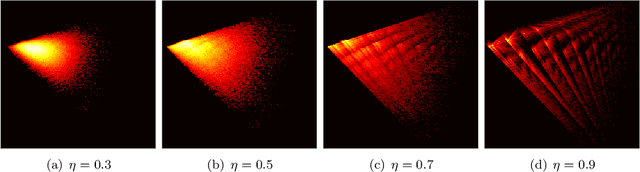
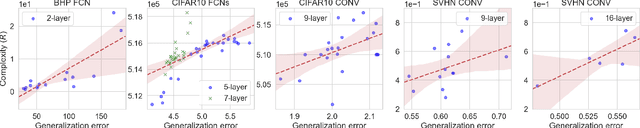
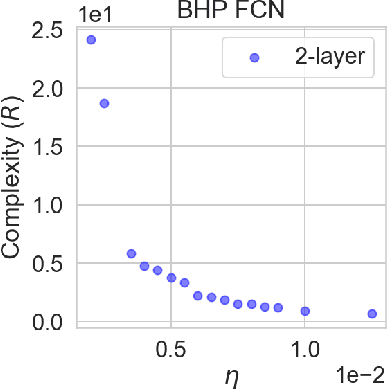
Understanding generalization in deep learning has been one of the major challenges in statistical learning theory over the last decade. While recent work has illustrated that the dataset and the training algorithm must be taken into account in order to obtain meaningful generalization bounds, it is still theoretically not clear which properties of the data and the algorithm determine the generalization performance. In this study, we approach this problem from a dynamical systems theory perspective and represent stochastic optimization algorithms as random iterated function systems (IFS). Well studied in the dynamical systems literature, under mild assumptions, such IFSs can be shown to be ergodic with an invariant measure that is often supported on sets with a fractal structure. As our main contribution, we prove that the generalization error of a stochastic optimization algorithm can be bounded based on the `complexity' of the fractal structure that underlies its invariant measure. Leveraging results from dynamical systems theory, we show that the generalization error can be explicitly linked to the choice of the algorithm (e.g., stochastic gradient descent -- SGD), algorithm hyperparameters (e.g., step-size, batch-size), and the geometry of the problem (e.g., Hessian of the loss). We further specialize our results to specific problems (e.g., linear/logistic regression, one hidden-layered neural networks) and algorithms (e.g., SGD and preconditioned variants), and obtain analytical estimates for our bound.For modern neural networks, we develop an efficient algorithm to compute the developed bound and support our theory with various experiments on neural networks.

Certifiably Robust Variational Autoencoders

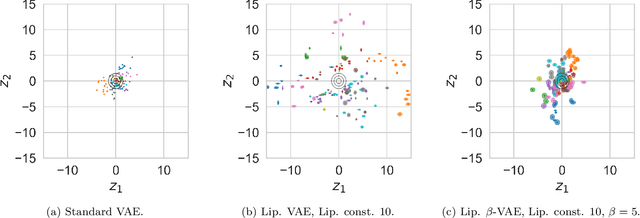
We introduce an approach for training Variational Autoencoders (VAEs) that are certifiably robust to adversarial attack. Specifically, we first derive actionable bounds on the minimal size of an input perturbation required to change a VAE's reconstruction by more than an allowed amount, with these bounds depending on certain key parameters such as the Lipschitz constants of the encoder and decoder. We then show how these parameters can be controlled, thereby providing a mechanism to ensure a priori that a VAE will attain a desired level of robustness. Moreover, we extend this to a complete practical approach for training such VAEs to ensure our criteria are met. Critically, our method allows one to specify a desired level of robustness upfront and then train a VAE that is guaranteed to achieve this robustness. We further demonstrate that these Lipschitz--constrained VAEs are more robust to attack than standard VAEs in practice.

Asymmetric Heavy Tails and Implicit Bias in Gaussian Noise Injections

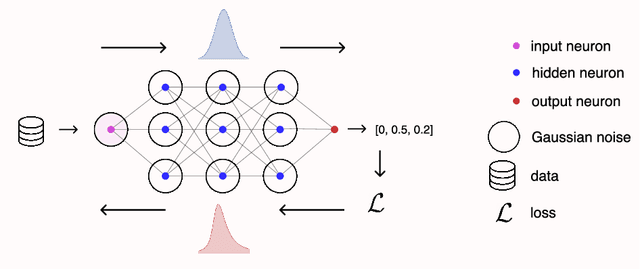
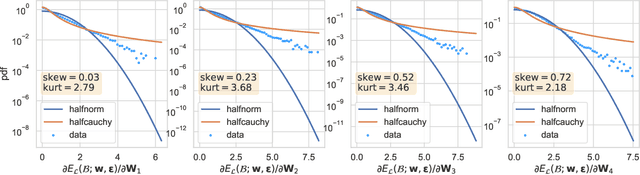
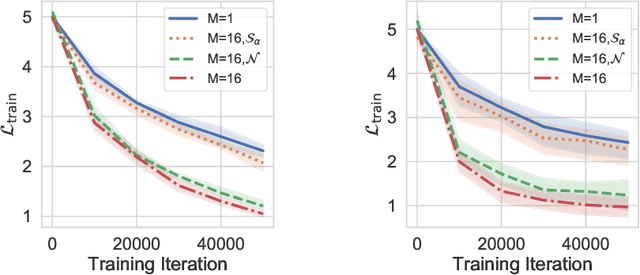
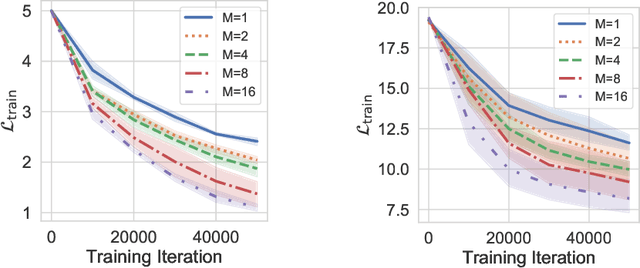
Gaussian noise injections (GNIs) are a family of simple and widely-used regularisation methods for training neural networks, where one injects additive or multiplicative Gaussian noise to the network activations at every iteration of the optimisation algorithm, which is typically chosen as stochastic gradient descent (SGD). In this paper we focus on the so-called `implicit effect' of GNIs, which is the effect of the injected noise on the dynamics of SGD. We show that this effect induces an asymmetric heavy-tailed noise on SGD gradient updates. In order to model this modified dynamics, we first develop a Langevin-like stochastic differential equation that is driven by a general family of asymmetric heavy-tailed noise. Using this model we then formally prove that GNIs induce an `implicit bias', which varies depending on the heaviness of the tails and the level of asymmetry. Our empirical results confirm that different types of neural networks trained with GNIs are well-modelled by the proposed dynamics and that the implicit effect of these injections induces a bias that degrades the performance of networks.

Explicit Regularisation in Gaussian Noise Injections

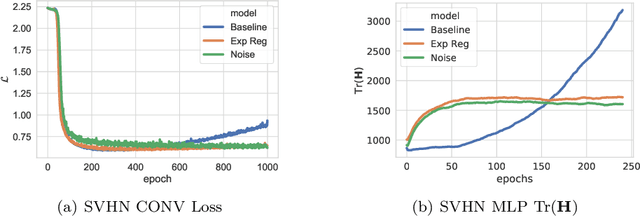
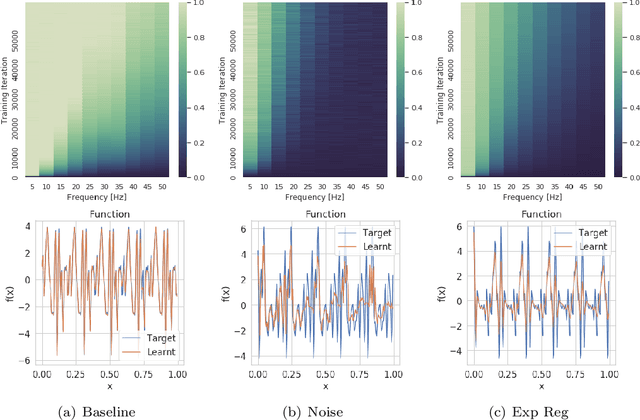
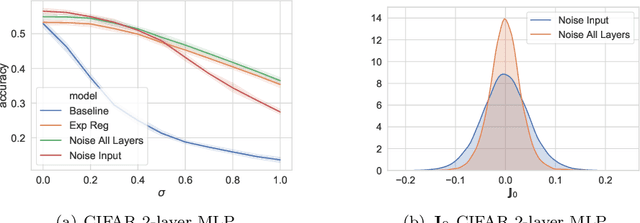
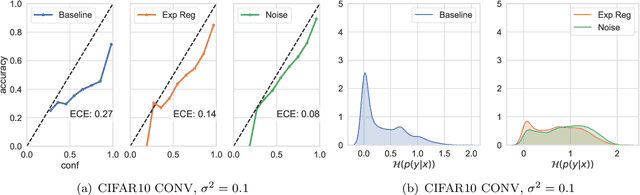
We study the regularisation induced in neural networks by Gaussian noise injections (GNIs). Though such injections have been extensively studied when applied to data, there have been few studies on understanding the regularising effect they induce when applied to network activations. Here we derive the explicit regulariser of GNIs, obtained by marginalising out the injected noise, and show that it is a form of Tikhonov regularisation which penalises functions with high-frequency components in the Fourier domain. We show analytically and empirically that such regularisation produces calibrated classifiers with large classification margins and that the explicit regulariser we derive is able to reproduce these effects.

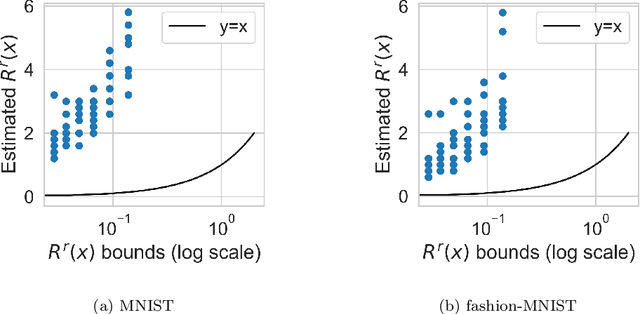
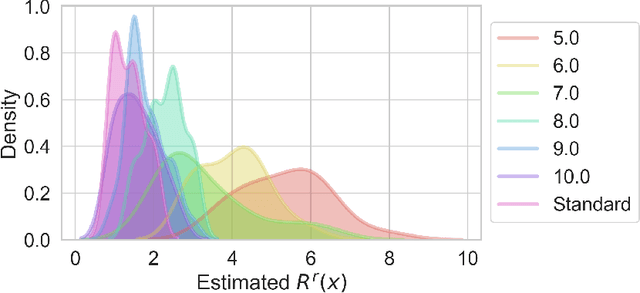
Towards a Theoretical Understanding of the Robustness of Variational Autoencoders

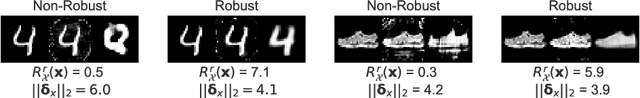
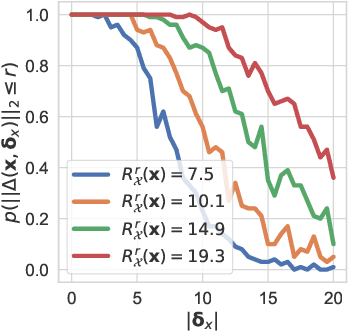
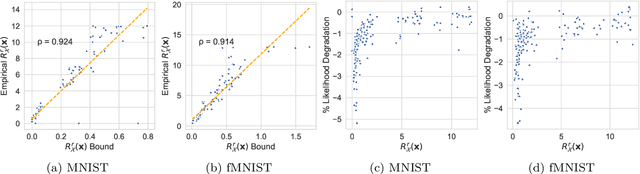
We make inroads into understanding the robustness of Variational Autoencoders (VAEs) to adversarial attacks and other input perturbations. While previous work has developed algorithmic approaches to attacking and defending VAEs, there remains a lack of formalization for what it means for a VAE to be robust. To address this, we develop a novel criterion for robustness in probabilistic models: $r$-robustness. We then use this to construct the first theoretical results for the robustness of VAEs, deriving margins in the input space for which we can provide guarantees about the resulting reconstruction. Informally, we are able to define a region within which any perturbation will produce a reconstruction that is similar to the original reconstruction. To support our analysis, we show that VAEs trained using disentangling methods not only score well under our robustness metrics, but that the reasons for this can be interpreted through our theoretical results.

Learning Bijective Feature Maps for Linear ICA

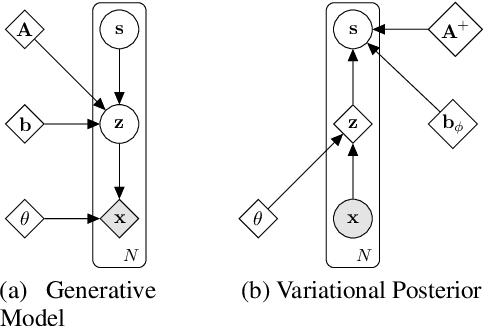
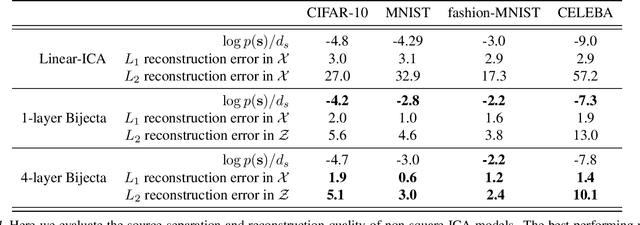
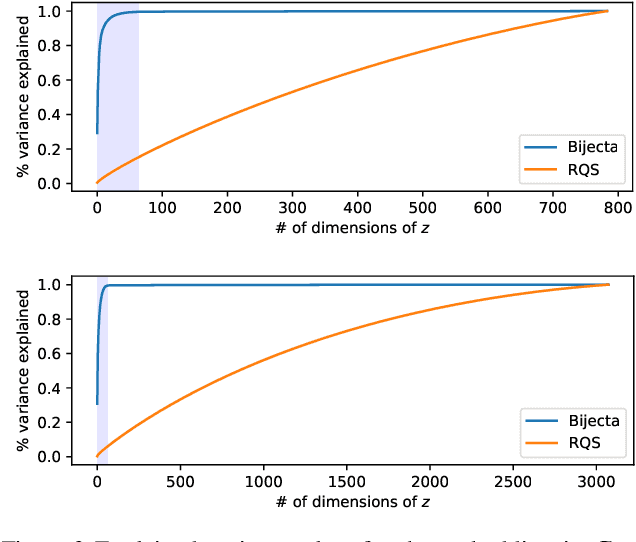
Separating high-dimensional data like images into independent latent factors remains an open research problem. Here we develop a method that jointly learns a linear independent component analysis (ICA) model with non-linear bijective feature maps. By combining these two methods, ICA can learn interpretable latent structure for images. For non-square ICA, where we assume the number of sources is less than the dimensionality of data, we achieve better unsupervised latent factor discovery than flow-based models and linear ICA. This performance scales to large image datasets such as CelebA.

Regularising Deep Networks with Deep Generative Models

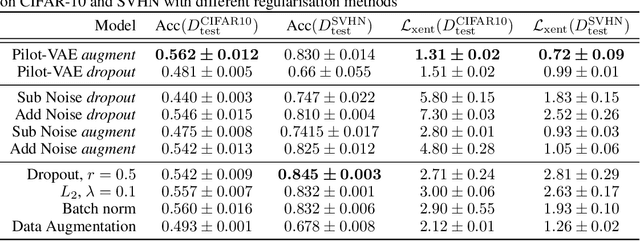
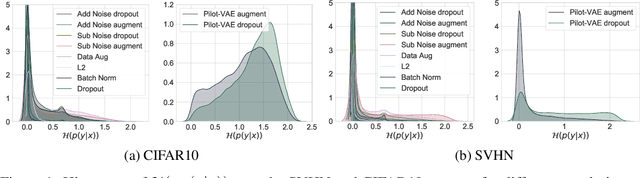
We develop a new method for regularising neural networks. We learn a probability distribution over the activations of all layers of the model and then insert imputed values into the network during training. We obtain a posterior for an arbitrary subset of activations conditioned on the remainder. This is a generalisation of data augmentation to the hidden layers of a network, and a form of data-aware dropout. We demonstrate that our training method leads to higher test accuracy and lower test-set cross-entropy for neural networks trained on CIFAR-10 and SVHN compared to standard regularisation baselines: our approach leads to networks with better calibrated uncertainty over the class posteriors all the while delivering greater test-set accuracy.

Disentangling Improves VAEs' Robustness to Adversarial Attacks

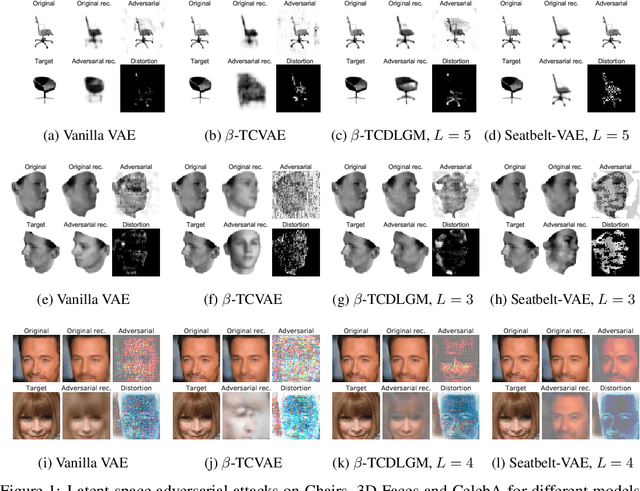
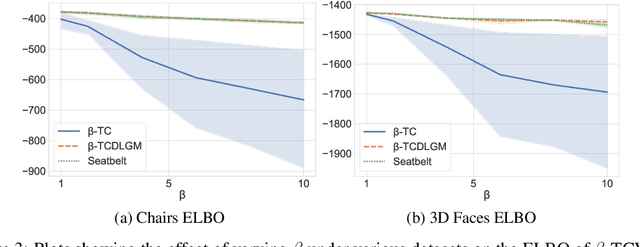
This paper is concerned with the robustness of VAEs to adversarial attacks. We highlight that conventional VAEs are brittle under attack but that methods recently introduced for disentanglement such as $\beta$-TCVAE (Chen et al., 2018) improve robustness, as demonstrated through a variety of previously proposed adversarial attacks (Tabacof et al. (2016); Gondim-Ribeiro et al. (2018); Kos et al.(2018)). This motivated us to develop Seatbelt-VAE, a new hierarchical disentangled VAE that is designed to be significantly more robust to adversarial attacks than existing approaches, while retaining high quality reconstructions.