Verifiable evaluations of machine learning models using zkSNARKs

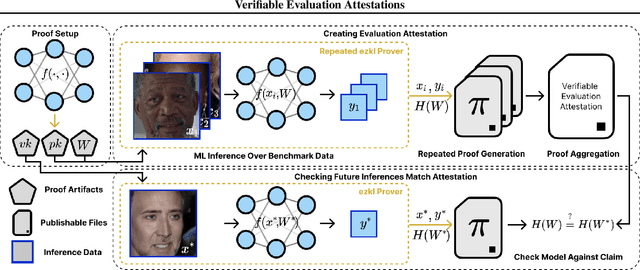
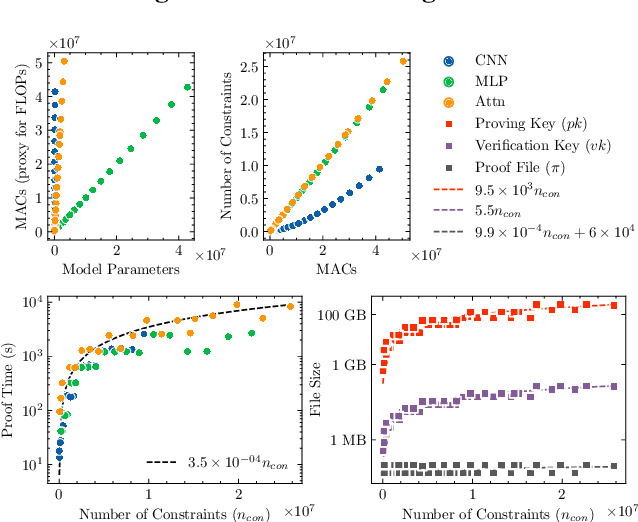
In a world of increasing closed-source commercial machine learning models, model evaluations from developers must be taken at face value. These benchmark results, whether over task accuracy, bias evaluations, or safety checks, are traditionally impossible to verify by a model end-user without the costly or impossible process of re-performing the benchmark on black-box model outputs. This work presents a method of verifiable model evaluation using model inference through zkSNARKs. The resulting zero-knowledge computational proofs of model outputs over datasets can be packaged into verifiable evaluation attestations showing that models with fixed private weights achieve stated performance or fairness metrics over public inputs. These verifiable attestations can be performed on any standard neural network model with varying compute requirements. For the first time, we demonstrate this across a sample of real-world models and highlight key challenges and design solutions. This presents a new transparency paradigm in the verifiable evaluation of private models.

Dimension of Marginals of Kronecker Product Models

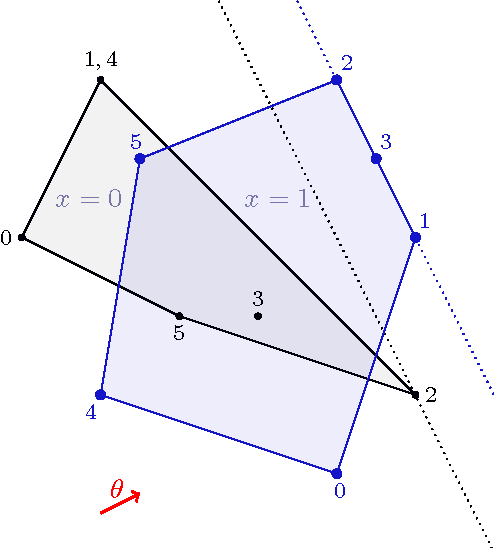
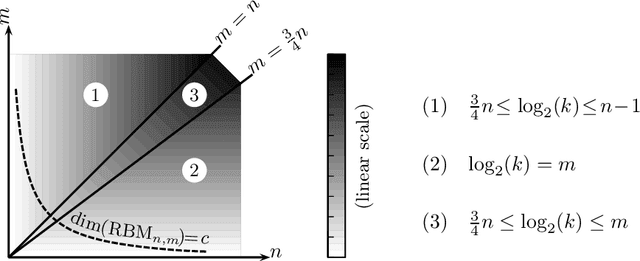
A Kronecker product model is the set of visible marginal probability distributions of an exponential family whose sufficient statistics matrix factorizes as a Kronecker product of two matrices, one for the visible variables and one for the hidden variables. We estimate the dimension of these models by the maximum rank of the Jacobian in the limit of large parameters. The limit is described by the tropical morphism; a piecewise linear map with pieces corresponding to slicings of the visible matrix by the normal fan of the hidden matrix. We obtain combinatorial conditions under which the model has the expected dimension, equal to the minimum of the number of natural parameters and the dimension of the ambient probability simplex. Additionally, we prove that the binary restricted Boltzmann machine always has the expected dimension.

When Does a Mixture of Products Contain a Product of Mixtures?

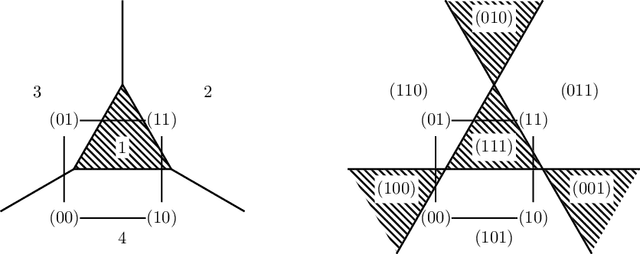
We derive relations between theoretical properties of restricted Boltzmann machines (RBMs), popular machine learning models which form the building blocks of deep learning models, and several natural notions from discrete mathematics and convex geometry. We give implications and equivalences relating RBM-representable probability distributions, perfectly reconstructible inputs, Hamming modes, zonotopes and zonosets, point configurations in hyperplane arrangements, linear threshold codes, and multi-covering numbers of hypercubes. As a motivating application, we prove results on the relative representational power of mixtures of product distributions and products of mixtures of pairs of product distributions (RBMs) that formally justify widely held intuitions about distributed representations. In particular, we show that a mixture of products requiring an exponentially larger number of parameters is needed to represent the probability distributions which can be obtained as products of mixtures.

Discrete Restricted Boltzmann Machines

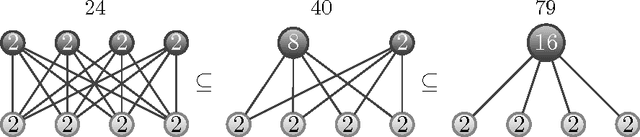
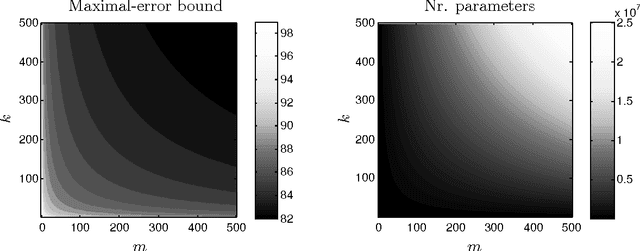
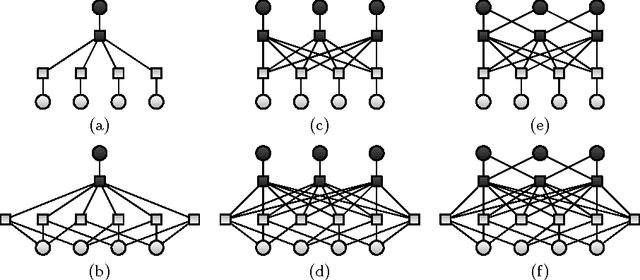
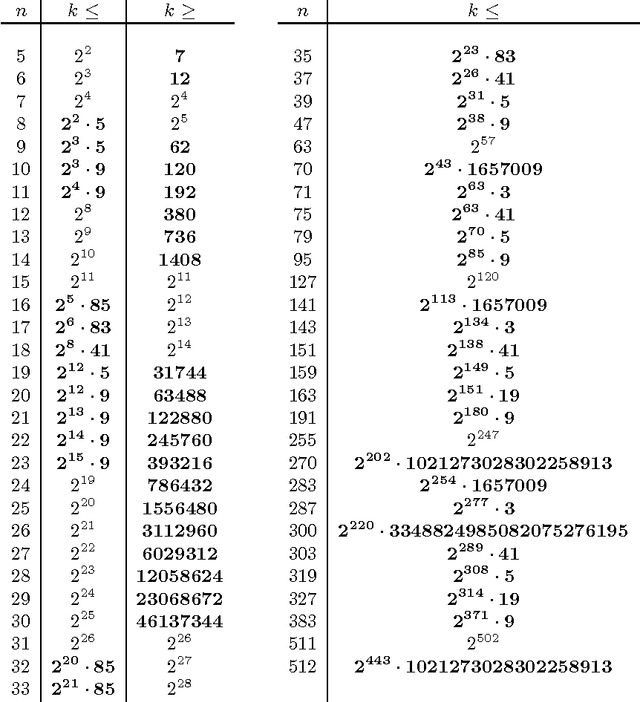
We describe discrete restricted Boltzmann machines: probabilistic graphical models with bipartite interactions between visible and hidden discrete variables. Examples are binary restricted Boltzmann machines and discrete naive Bayes models. We detail the inference functions and distributed representations arising in these models in terms of configurations of projected products of simplices and normal fans of products of simplices. We bound the number of hidden variables, depending on the cardinalities of their state spaces, for which these models can approximate any probability distribution on their visible states to any given accuracy. In addition, we use algebraic methods and coding theory to compute their dimension.

Kernels and Submodels of Deep Belief Networks

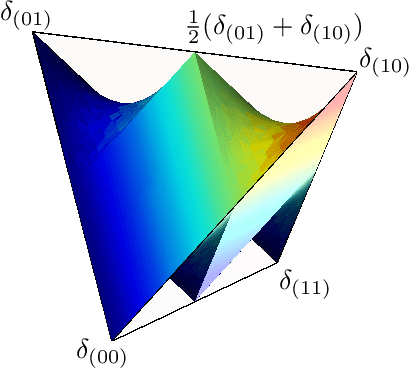
We study the mixtures of factorizing probability distributions represented as visible marginal distributions in stochastic layered networks. We take the perspective of kernel transitions of distributions, which gives a unified picture of distributed representations arising from Deep Belief Networks (DBN) and other networks without lateral connections. We describe combinatorial and geometric properties of the set of kernels and products of kernels realizable by DBNs as the network parameters vary. We describe explicit classes of probability distributions, including exponential families, that can be learned by DBNs. We use these submodels to bound the maximal and the expected Kullback-Leibler approximation errors of DBNs from above depending on the number of hidden layers and units that they contain.

Geometry of the restricted Boltzmann machine

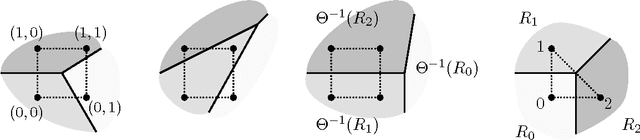
The restricted Boltzmann machine is a graphical model for binary random variables. Based on a complete bipartite graph separating hidden and observed variables, it is the binary analog to the factor analysis model. We study this graphical model from the perspectives of algebraic statistics and tropical geometry, starting with the observation that its Zariski closure is a Hadamard power of the first secant variety of the Segre variety of projective lines. We derive a dimension formula for the tropicalized model, and we use it to show that the restricted Boltzmann machine is identifiable in many cases. Our methods include coding theory and geometry of linear threshold functions.

Relations among conditional probabilities

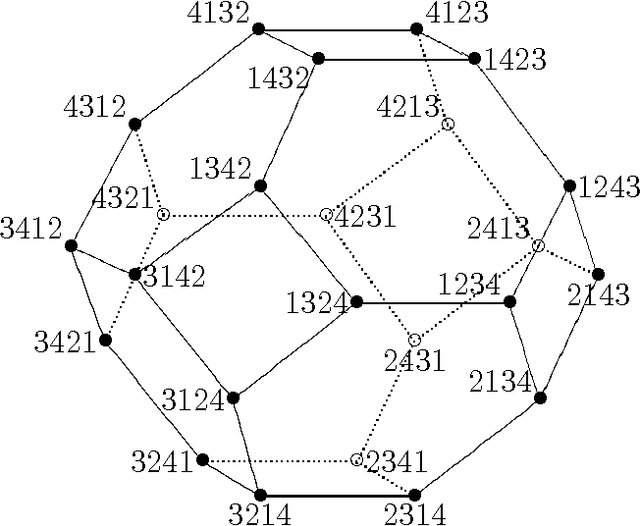
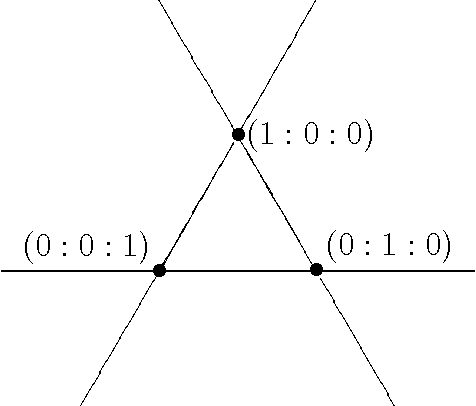
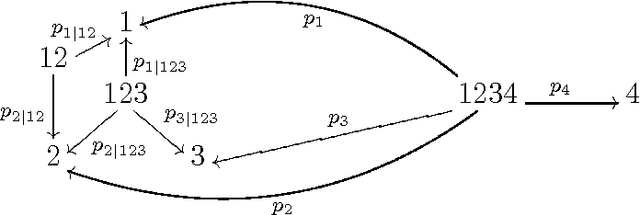
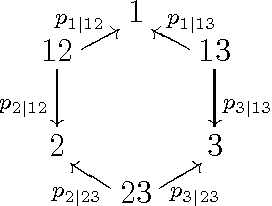
We describe a Groebner basis of relations among conditional probabilities in a discrete probability space, with any set of conditioned-upon events. They may be specialized to the partially-observed random variable case, the purely conditional case, and other special cases. We also investigate the connection to generalized permutohedra and describe a conditional probability simplex.