When Does a Mixture of Products Contain a Product of Mixtures?

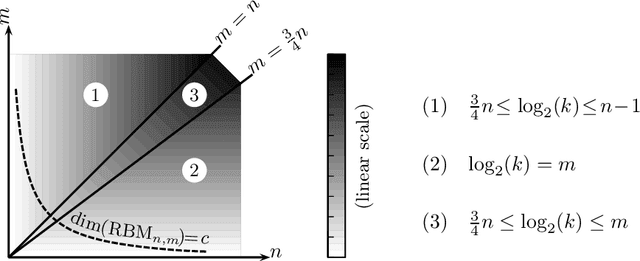
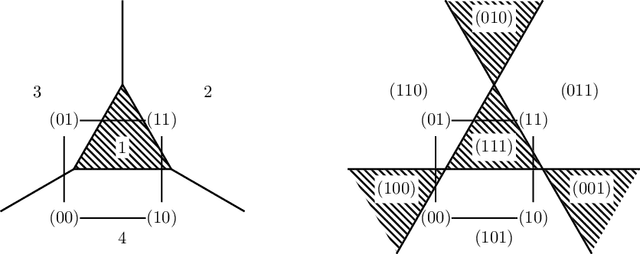
We derive relations between theoretical properties of restricted Boltzmann machines (RBMs), popular machine learning models which form the building blocks of deep learning models, and several natural notions from discrete mathematics and convex geometry. We give implications and equivalences relating RBM-representable probability distributions, perfectly reconstructible inputs, Hamming modes, zonotopes and zonosets, point configurations in hyperplane arrangements, linear threshold codes, and multi-covering numbers of hypercubes. As a motivating application, we prove results on the relative representational power of mixtures of product distributions and products of mixtures of pairs of product distributions (RBMs) that formally justify widely held intuitions about distributed representations. In particular, we show that a mixture of products requiring an exponentially larger number of parameters is needed to represent the probability distributions which can be obtained as products of mixtures.

Scaling of Model Approximation Errors and Expected Entropy Distances

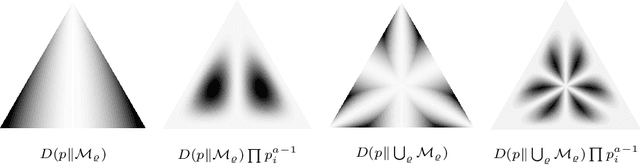
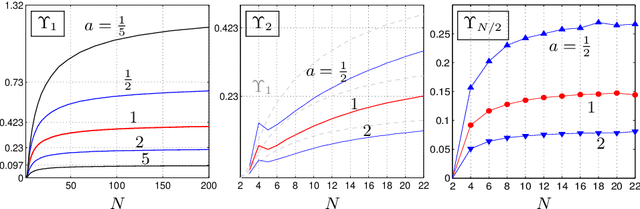
We compute the expected value of the Kullback-Leibler divergence to various fundamental statistical models with respect to canonical priors on the probability simplex. We obtain closed formulas for the expected model approximation errors, depending on the dimension of the models and the cardinalities of their sample spaces. For the uniform prior, the expected divergence from any model containing the uniform distribution is bounded by a constant $1-\gamma$, and for the models that we consider, this bound is approached if the state space is very large and the models' dimension does not grow too fast. For Dirichlet priors the expected divergence is bounded in a similar way, if the concentration parameters take reasonable values. These results serve as reference values for more complicated statistical models.

Kernels and Submodels of Deep Belief Networks

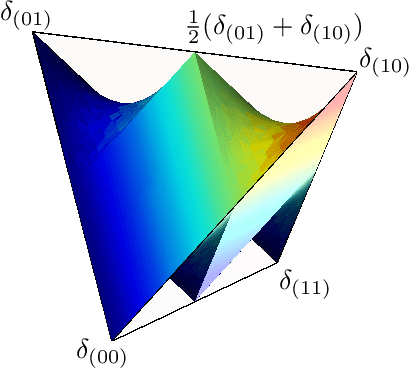
We study the mixtures of factorizing probability distributions represented as visible marginal distributions in stochastic layered networks. We take the perspective of kernel transitions of distributions, which gives a unified picture of distributed representations arising from Deep Belief Networks (DBN) and other networks without lateral connections. We describe combinatorial and geometric properties of the set of kernels and products of kernels realizable by DBNs as the network parameters vary. We describe explicit classes of probability distributions, including exponential families, that can be learned by DBNs. We use these submodels to bound the maximal and the expected Kullback-Leibler approximation errors of DBNs from above depending on the number of hidden layers and units that they contain.