Scaling of Model Approximation Errors and Expected Entropy Distances
Paper and Code
Feb 25, 2013
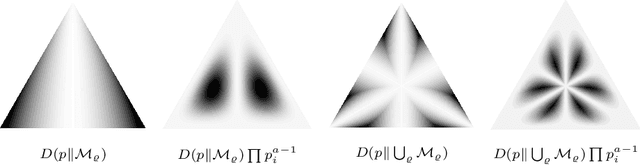
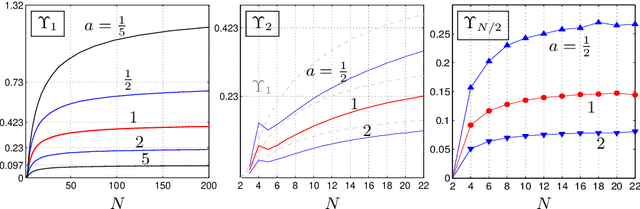
We compute the expected value of the Kullback-Leibler divergence to various fundamental statistical models with respect to canonical priors on the probability simplex. We obtain closed formulas for the expected model approximation errors, depending on the dimension of the models and the cardinalities of their sample spaces. For the uniform prior, the expected divergence from any model containing the uniform distribution is bounded by a constant $1-\gamma$, and for the models that we consider, this bound is approached if the state space is very large and the models' dimension does not grow too fast. For Dirichlet priors the expected divergence is bounded in a similar way, if the concentration parameters take reasonable values. These results serve as reference values for more complicated statistical models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge