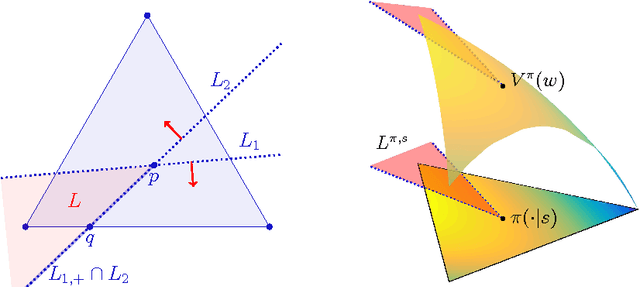
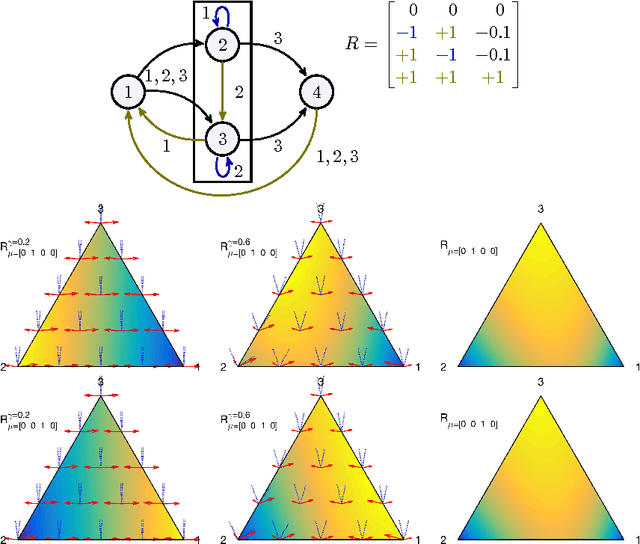
Geometry of Policy Improvement

We investigate the geometry of optimal memoryless time independent decision making in relation to the amount of information that the acting agent has about the state of the system. We show that the expected long term reward, discounted or per time step, is maximized by policies that randomize among at most $k$ actions whenever at most $k$ world states are consistent with the agent's observation. Moreover, we show that the expected reward per time step can be studied in terms of the expected discounted reward. Our main tool is a geometric version of the policy improvement lemma, which identifies a polyhedral cone of policy changes in which the state value function increases for all states.

Hierarchical Models as Marginals of Hierarchical Models

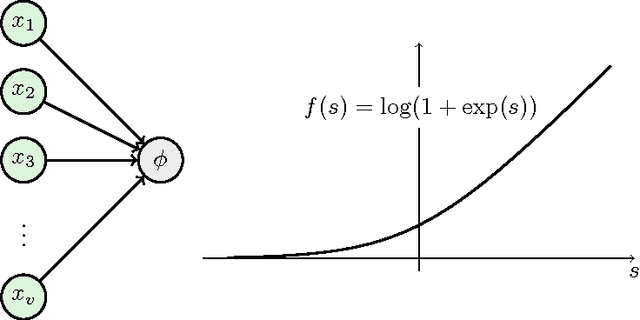
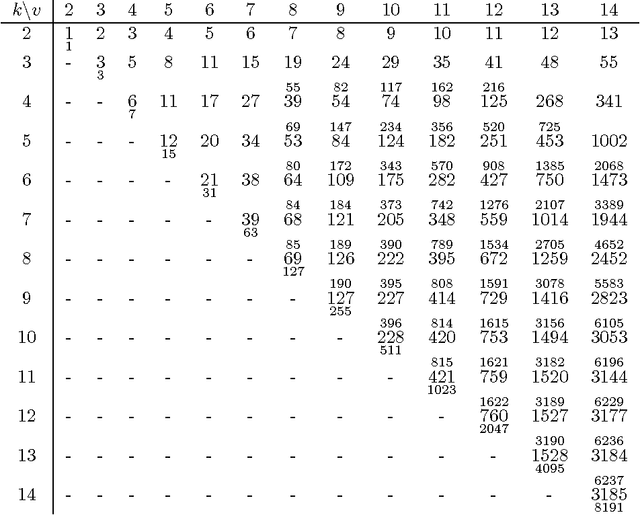
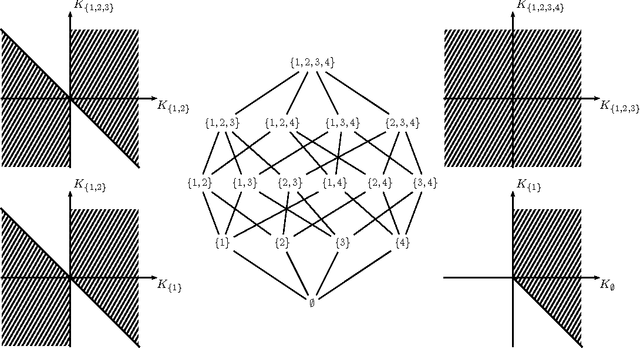
We investigate the representation of hierarchical models in terms of marginals of other hierarchical models with smaller interactions. We focus on binary variables and marginals of pairwise interaction models whose hidden variables are conditionally independent given the visible variables. In this case the problem is equivalent to the representation of linear subspaces of polynomials by feedforward neural networks with soft-plus computational units. We show that every hidden variable can freely model multiple interactions among the visible variables, which allows us to generalize and improve previous results. In particular, we show that a restricted Boltzmann machine with less than $[ 2(\log(v)+1) / (v+1) ] 2^v-1$ hidden binary variables can approximate every distribution of $v$ visible binary variables arbitrarily well, compared to $2^{v-1}-1$ from the best previously known result.

Quantifying Morphological Computation based on an Information Decomposition of the Sensorimotor Loop

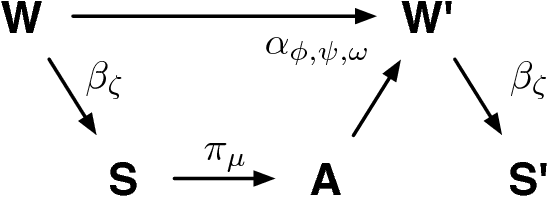
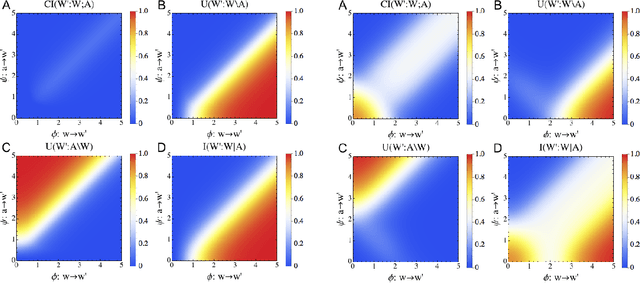
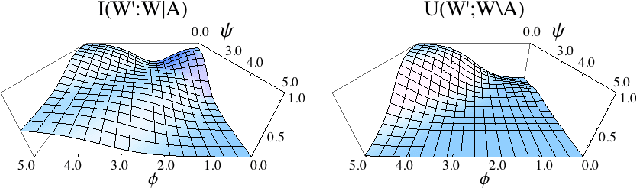
The question how an agent is affected by its embodiment has attracted growing attention in recent years. A new field of artificial intelligence has emerged, which is based on the idea that intelligence cannot be understood without taking into account embodiment. We believe that a formal approach to quantifying the embodiment's effect on the agent's behaviour is beneficial to the fields of artificial life and artificial intelligence. The contribution of an agent's body and environment to its behaviour is also known as morphological computation. Therefore, in this work, we propose a quantification of morphological computation, which is based on an information decomposition of the sensorimotor loop into shared, unique and synergistic information. In numerical simulation based on a formal representation of the sensorimotor loop, we show that the unique information of the body and environment is a good measure for morphological computation. The results are compared to our previously derived quantification of morphological computation.

Expressive Power and Approximation Errors of Restricted Boltzmann Machines

We present explicit classes of probability distributions that can be learned by Restricted Boltzmann Machines (RBMs) depending on the number of units that they contain, and which are representative for the expressive power of the model. We use this to show that the maximal Kullback-Leibler divergence to the RBM model with $n$ visible and $m$ hidden units is bounded from above by $n - \left\lfloor \log(m+1) \right\rfloor - \frac{m+1}{2^{\left\lfloor\log(m+1)\right\rfloor}} \approx (n -1) - \log(m+1)$. In this way we can specify the number of hidden units that guarantees a sufficiently rich model containing different classes of distributions and respecting a given error tolerance.

Maximal Information Divergence from Statistical Models defined by Neural Networks

We review recent results about the maximal values of the Kullback-Leibler information divergence from statistical models defined by neural networks, including naive Bayes models, restricted Boltzmann machines, deep belief networks, and various classes of exponential families. We illustrate approaches to compute the maximal divergence from a given model starting from simple sub- or super-models. We give a new result for deep and narrow belief networks with finite-valued units.

Scaling of Model Approximation Errors and Expected Entropy Distances

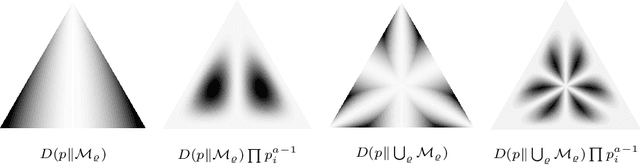
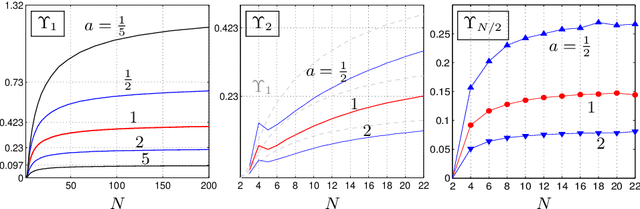
We compute the expected value of the Kullback-Leibler divergence to various fundamental statistical models with respect to canonical priors on the probability simplex. We obtain closed formulas for the expected model approximation errors, depending on the dimension of the models and the cardinalities of their sample spaces. For the uniform prior, the expected divergence from any model containing the uniform distribution is bounded by a constant $1-\gamma$, and for the models that we consider, this bound is approached if the state space is very large and the models' dimension does not grow too fast. For Dirichlet priors the expected divergence is bounded in a similar way, if the concentration parameters take reasonable values. These results serve as reference values for more complicated statistical models.