Convergence Properties of Natural Gradient Descent for Minimizing KL Divergence

The Kullback-Leibler (KL) divergence plays a central role in probabilistic machine learning, where it commonly serves as the canonical loss function. Optimization in such settings is often performed over the probability simplex, where the choice of parameterization significantly impacts convergence. In this work, we study the problem of minimizing the KL divergence and analyze the behavior of gradient-based optimization algorithms under two dual coordinate systems within the framework of information geometry$-$ the exponential family ($\theta$ coordinates) and the mixture family ($\eta$ coordinates). We compare Euclidean gradient descent (GD) in these coordinates with the coordinate-invariant natural gradient descent (NGD), where the natural gradient is a Riemannian gradient that incorporates the intrinsic geometry of the parameter space. In continuous time, we prove that the convergence rates of GD in the $\theta$ and $\eta$ coordinates provide lower and upper bounds, respectively, on the convergence rate of NGD. Moreover, under affine reparameterizations of the dual coordinates, the convergence rates of GD in $\eta$ and $\theta$ coordinates can be scaled to $2c$ and $\frac{2}{c}$, respectively, for any $c>0$, while NGD maintains a fixed convergence rate of $2$, remaining invariant to such transformations and sandwiched between them. Although this suggests that NGD may not exhibit uniformly superior convergence in continuous time, we demonstrate that its advantages become pronounced in discrete time, where it achieves faster convergence and greater robustness to noise, outperforming GD. Our analysis hinges on bounding the spectrum and condition number of the Hessian of the KL divergence at the optimum, which coincides with the Fisher information matrix.

Wasserstein KL-divergence for Gaussian distributions

We introduce a new version of the KL-divergence for Gaussian distributions which is based on Wasserstein geometry and referred to as WKL-divergence. We show that this version is consistent with the geometry of the sample space ${\Bbb R}^n$. In particular, we can evaluate the WKL-divergence of the Dirac measures concentrated in two points which turns out to be proportional to the squared distance between these points.

Analyzing Multimodal Integration in the Variational Autoencoder from an Information-Theoretic Perspective

Human perception is inherently multimodal. We integrate, for instance, visual, proprioceptive and tactile information into one experience. Hence, multimodal learning is of importance for building robotic systems that aim at robustly interacting with the real world. One potential model that has been proposed for multimodal integration is the multimodal variational autoencoder. A variational autoencoder (VAE) consists of two networks, an encoder that maps the data to a stochastic latent space and a decoder that reconstruct this data from an element of this latent space. The multimodal VAE integrates inputs from different modalities at two points in time in the latent space and can thereby be used as a controller for a robotic agent. Here we use this architecture and introduce information-theoretic measures in order to analyze how important the integration of the different modalities are for the reconstruction of the input data. Therefore we calculate two different types of measures, the first type is called single modality error and assesses how important the information from a single modality is for the reconstruction of this modality or all modalities. Secondly, the measures named loss of precision calculate the impact that missing information from only one modality has on the reconstruction of this modality or the whole vector. The VAE is trained via the evidence lower bound, which can be written as a sum of two different terms, namely the reconstruction and the latent loss. The impact of the latent loss can be weighted via an additional variable, which has been introduced to combat posterior collapse. Here we train networks with four different weighting schedules and analyze them with respect to their capabilities for multimodal integration.

A Concise Mathematical Description of Active Inference in Discrete Time

In this paper we present a concise mathematical description of active inference in discrete time. The main part of the paper serves as a general introduction to the topic, including an example illustrating the theory on action selection. In the appendix the more subtle mathematical details are discussed. This part is aimed at readers who have already studied the active inference literature but struggle to make sense of the mathematical details and derivations. Throughout the whole manuscript, special attention has been paid to adopting notation that is both precise and in line with standard mathematical texts. All equations and derivations are linked to specific equation numbers in other popular text on the topic. Furthermore, Python code is provided that implements the action selection mechanism described in this paper and is compatible with pymdp environments.

On the Fisher-Rao Gradient of the Evidence Lower Bound

This article studies the Fisher-Rao gradient, also referred to as the natural gradient, of the evidence lower bound, the ELBO, which plays a crucial role within the theory of the Variational Autonecoder, the Helmholtz Machine and the Free Energy Principle. The natural gradient of the ELBO is related to the natural gradient of the Kullback-Leibler divergence from a target distribution, the prime objective function of learning. Based on invariance properties of gradients within information geometry, conditions on the underlying model are provided that ensure the equivalence of minimising the prime objective function and the maximisation of the ELBO.

Inversion of Bayesian Networks

Variational autoencoders and Helmholtz machines use a recognition network (encoder) to approximate the posterior distribution of a generative model (decoder). In this paper we study the necessary and sufficient properties of a recognition network so that it can model the true posterior distribution exactly. These results are derived in the general context of probabilistic graphical modelling / Bayesian networks, for which the network represents a set of conditional independence statements. We derive both global conditions, in terms of d-separation, and local conditions for the recognition network to have the desired qualities. It turns out that for the local conditions the property perfectness (for every node, all parents are joined) plays an important role.

Invariance Properties of the Natural Gradient in Overparametrised Systems

The natural gradient field is a vector field that lives on a model equipped with a distinguished Riemannian metric, e.g. the Fisher-Rao metric, and represents the direction of steepest ascent of an objective function on the model with respect to this metric. In practice, one tries to obtain the corresponding direction on the parameter space by multiplying the ordinary gradient by the inverse of the Gram matrix associated with the metric. We refer to this vector on the parameter space as the natural parameter gradient. In this paper we study when the pushforward of the natural parameter gradient is equal to the natural gradient. Furthermore we investigate the invariance properties of the natural parameter gradient. Both questions are addressed in an overparametrised setting.

Natural Wake-Sleep Algorithm

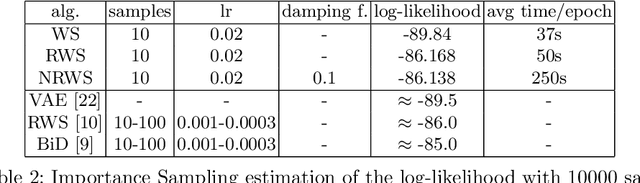
The benefits of using the natural gradient are well known in a wide range of optimization problems. However, for the training of common neural networks the resulting increase in computational complexity sets a limitation to its practical application. Helmholtz Machines are a particular type of generative model composed of two Sigmoid Belief Networks (SBNs), acting as an encoder and a decoder, commonly trained using the Wake-Sleep (WS) algorithm and its reweighted version RWS. For SBNs, it has been shown how the locality of the connections in the graphical structure induces sparsity in the Fisher information matrix. The resulting block diagonal structure can be efficiently exploited to reduce the computational complexity of the Fisher matrix inversion and thus compute the natural gradient exactly, without the need of approximations. We present a geometric adaptation of well-known methods from the literature, introducing the Natural Wake-Sleep (NWS) and the Natural Reweighted Wake-Sleep (NRWS) algorithms. We present an experimental analysis of the novel geometrical algorithms based on the convergence speed and the value of the log-likelihood, both with respect to the number of iterations and the time complexity and demonstrating improvements on these aspects over their respective non-geometric baselines.

On the Locality of the Natural Gradient for Deep Learning

We study the natural gradient method for learning in deep Bayesian networks, including neural networks. There are two natural geometries associated with such learning systems consisting of visible and hidden units. One geometry is related to the full system, the other one to the visible sub-system. These two geometries imply different natural gradients. In a first step, we demonstrate a great simplification of the natural gradient with respect to the first geometry, due to locality properties of the Fisher information matrix. This simplification does not directly translate to a corresponding simplification with respect to the second geometry. We develop the theory for studying the relation between the two versions of the natural gradient and outline a method for the simplification of the natural gradient with respect to the second geometry based on the first one. This method suggests to incorporate a recognition model as an auxiliary model for the efficient application of the natural gradient method in deep networks.

Comparing Information-Theoretic Measures of Complexity in Boltzmann Machines

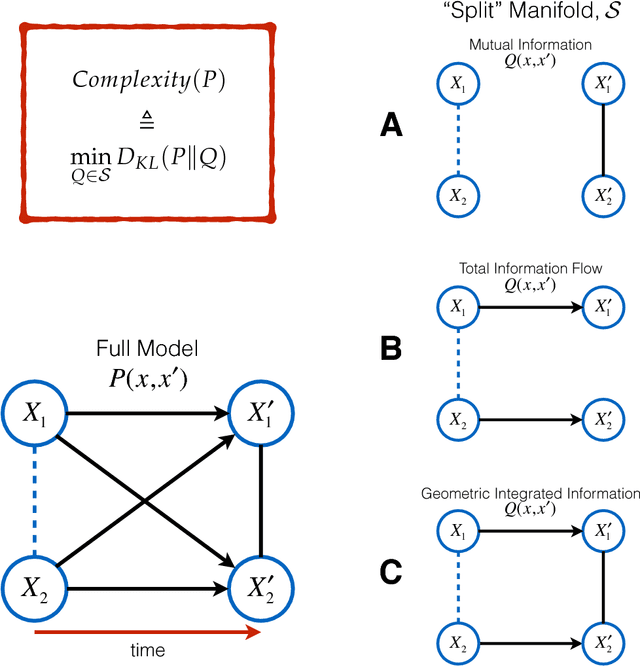
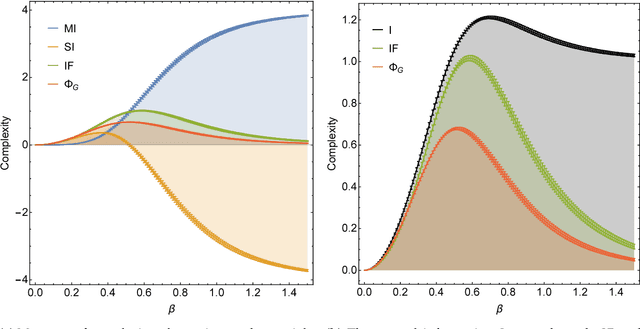
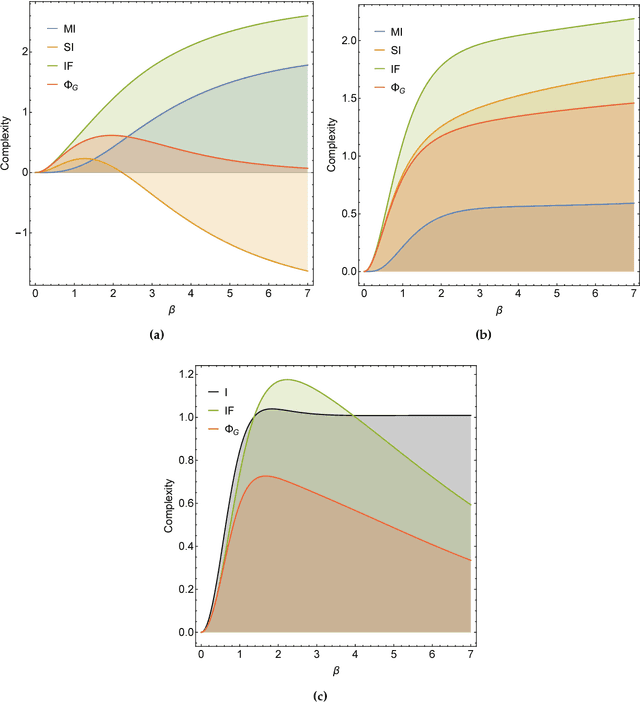
In the past three decades, many theoretical measures of complexity have been proposed to help understand complex systems. In this work, for the first time, we place these measures on a level playing field, to explore the qualitative similarities and differences between them, and their shortcomings. Specifically, using the Boltzmann machine architecture (a fully connected recurrent neural network) with uniformly distributed weights as our model of study, we numerically measure how complexity changes as a function of network dynamics and network parameters. We apply an extension of one such information-theoretic measure of complexity to understand incremental Hebbian learning in Hopfield networks, a fully recurrent architecture model of autoassociative memory. In the course of Hebbian learning, the total information flow reflects a natural upward trend in complexity as the network attempts to learn more and more patterns.