Csongor Várady
Romanian Institute for Science and Technology University, Cluj-Napoca, Romania, Max Planck Institute for Mathematics in the Sciences, Leipzig, Germany
Natural Wake-Sleep Algorithm
Aug 15, 2020


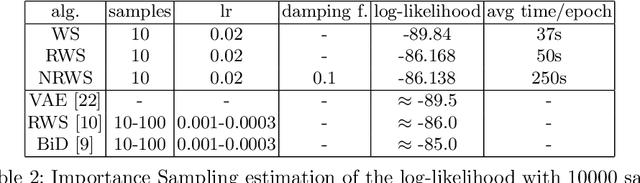
Abstract:The benefits of using the natural gradient are well known in a wide range of optimization problems. However, for the training of common neural networks the resulting increase in computational complexity sets a limitation to its practical application. Helmholtz Machines are a particular type of generative model composed of two Sigmoid Belief Networks (SBNs), acting as an encoder and a decoder, commonly trained using the Wake-Sleep (WS) algorithm and its reweighted version RWS. For SBNs, it has been shown how the locality of the connections in the graphical structure induces sparsity in the Fisher information matrix. The resulting block diagonal structure can be efficiently exploited to reduce the computational complexity of the Fisher matrix inversion and thus compute the natural gradient exactly, without the need of approximations. We present a geometric adaptation of well-known methods from the literature, introducing the Natural Wake-Sleep (NWS) and the Natural Reweighted Wake-Sleep (NRWS) algorithms. We present an experimental analysis of the novel geometrical algorithms based on the convergence speed and the value of the log-likelihood, both with respect to the number of iterations and the time complexity and demonstrating improvements on these aspects over their respective non-geometric baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge