Automatic Feature Extraction for Heartbeat Anomaly Detection

We focus on automatic feature extraction for raw audio heartbeat sounds, aimed at anomaly detection applications in healthcare. We learn features with the help of an autoencoder composed by a 1D non-causal convolutional encoder and a WaveNet decoder trained with a modified objective based on variational inference, employing the Maximum Mean Discrepancy (MMD). Moreover we model the latent distribution using a Gaussian chain graphical model to capture temporal correlations which characterize the encoded signals. After training the autoencoder on the reconstruction task in a unsupervised manner, we test the significance of the learned latent representations by training an SVM to predict anomalies. We evaluate the methods on a problem proposed by the PASCAL Classifying Heart Sounds Challenge and we compare with results in the literature.

Lagrangian and Hamiltonian Mechanics for Probabilities on the Statistical Manifold

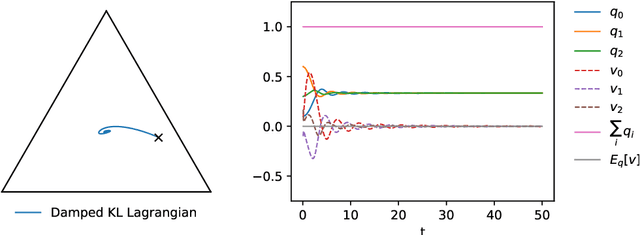
We provide an Information-Geometric formulation of Classical Mechanics on the Riemannian manifold of probability distributions, which is an affine manifold endowed with a dually-flat connection. In a non-parametric formalism, we consider the full set of positive probability functions on a finite sample space, and we provide a specific expression for the tangent and cotangent spaces over the statistical manifold, in terms of a Hilbert bundle structure that we call the Statistical Bundle. In this setting, we compute velocities and accelerations of a one-dimensional statistical model using the canonical dual pair of parallel transports and define a coherent formalism for Lagrangian and Hamiltonian mechanics on the bundle. Finally, in a series of examples, we show how our formalism provides a consistent framework for accelerated natural gradient dynamics on the probability simplex, paving the way for direct applications in optimization, game theory and neural networks.

Natural Wake-Sleep Algorithm

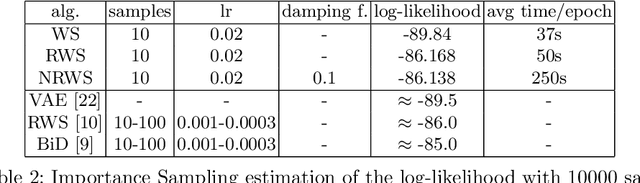
The benefits of using the natural gradient are well known in a wide range of optimization problems. However, for the training of common neural networks the resulting increase in computational complexity sets a limitation to its practical application. Helmholtz Machines are a particular type of generative model composed of two Sigmoid Belief Networks (SBNs), acting as an encoder and a decoder, commonly trained using the Wake-Sleep (WS) algorithm and its reweighted version RWS. For SBNs, it has been shown how the locality of the connections in the graphical structure induces sparsity in the Fisher information matrix. The resulting block diagonal structure can be efficiently exploited to reduce the computational complexity of the Fisher matrix inversion and thus compute the natural gradient exactly, without the need of approximations. We present a geometric adaptation of well-known methods from the literature, introducing the Natural Wake-Sleep (NWS) and the Natural Reweighted Wake-Sleep (NRWS) algorithms. We present an experimental analysis of the novel geometrical algorithms based on the convergence speed and the value of the log-likelihood, both with respect to the number of iterations and the time complexity and demonstrating improvements on these aspects over their respective non-geometric baselines.

Improved Slice-wise Tumour Detection in Brain MRIs by Computing Dissimilarities between Latent Representations

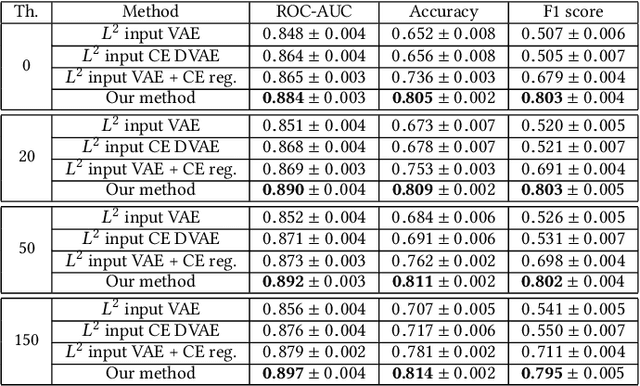
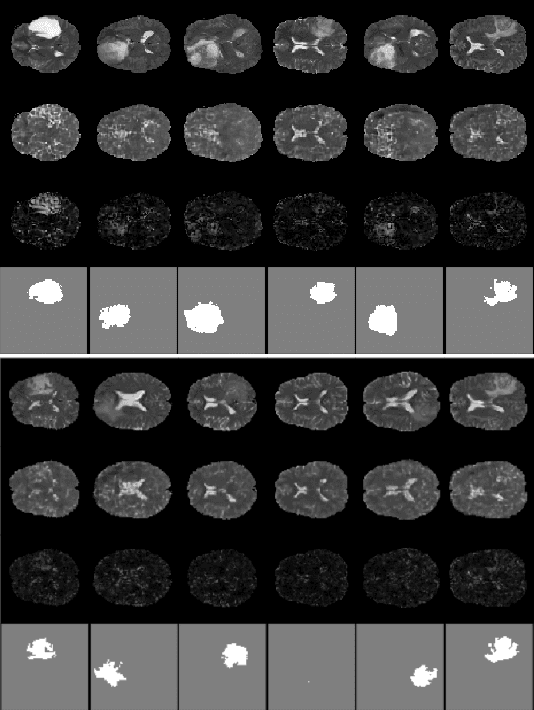
Anomaly detection for Magnetic Resonance Images (MRIs) can be solved with unsupervised methods by learning the distribution of healthy images and identifying anomalies as outliers. In presence of an additional dataset of unlabelled data containing also anomalies, the task can be framed as a semi-supervised task with negative and unlabelled sample points. Recently, in Albu et al., 2020, we have proposed a slice-wise semi-supervised method for tumour detection based on the computation of a dissimilarity function in the latent space of a Variational AutoEncoder, trained on unlabelled data. The dissimilarity is computed between the encoding of the image and the encoding of its reconstruction obtained through a different autoencoder trained only on healthy images. In this paper we present novel and improved results for our method, obtained by training the Variational AutoEncoders on a subset of the HCP and BRATS-2018 datasets and testing on the remaining individuals. We show that by training the models on higher resolution images and by improving the quality of the reconstructions, we obtain results which are comparable with different baselines, which employ a single VAE trained on healthy individuals. As expected, the performance of our method increases with the size of the threshold used to determine the presence of an anomaly.

Parameters Estimation from the 21 cm signal using Variational Inference

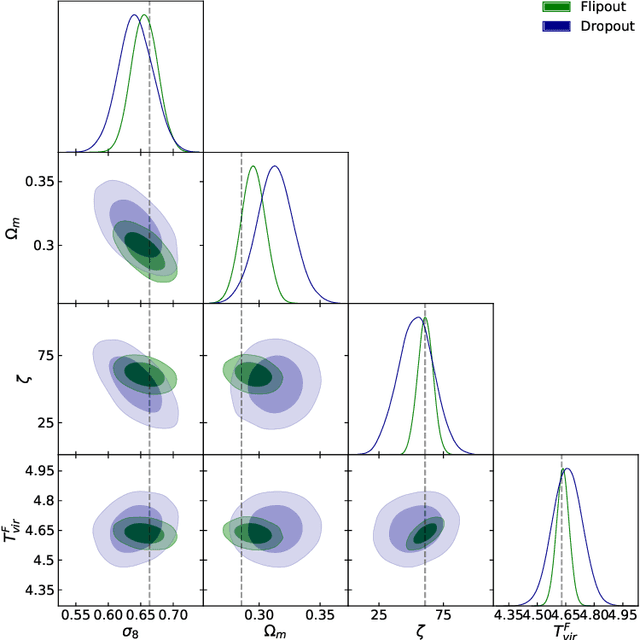
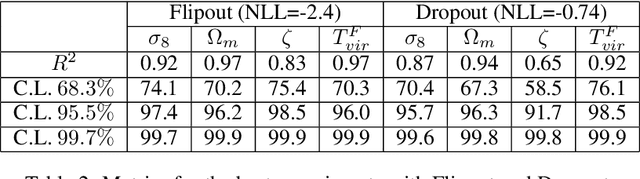
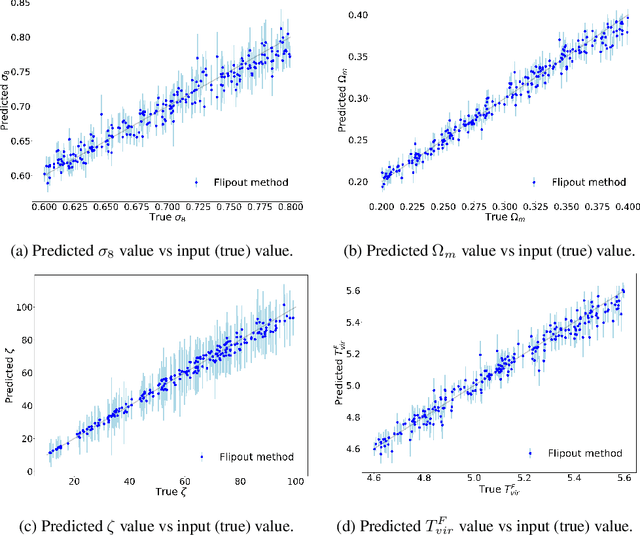
Upcoming experiments such as Hydrogen Epoch of Reionization Array (HERA) and Square Kilometre Array (SKA) are intended to measure the 21cm signal over a wide range of redshifts, representing an incredible opportunity in advancing our understanding about the nature of cosmic Reionization. At the same time these kind of experiments will present new challenges in processing the extensive amount of data generated, calling for the development of automated methods capable of precisely estimating physical parameters and their uncertainties. In this paper we employ Variational Inference, and in particular Bayesian Neural Networks, as an alternative to MCMC in 21 cm observations to report credible estimations for cosmological and astrophysical parameters and assess the correlations among them.

Natural Alpha Embeddings

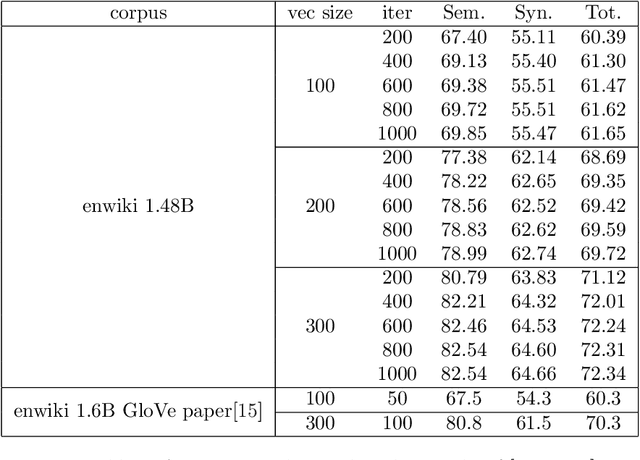
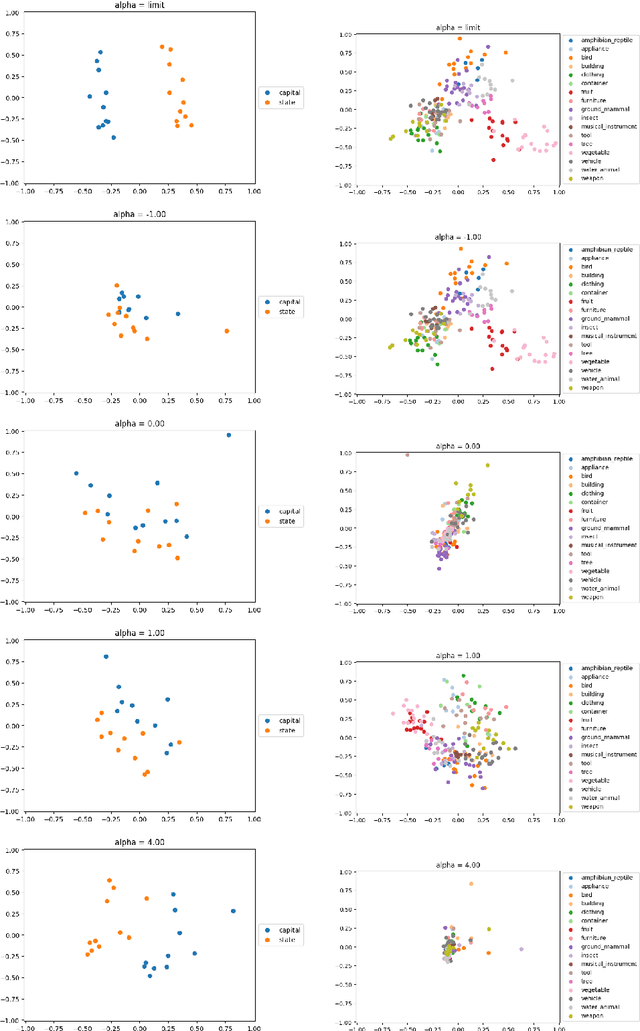
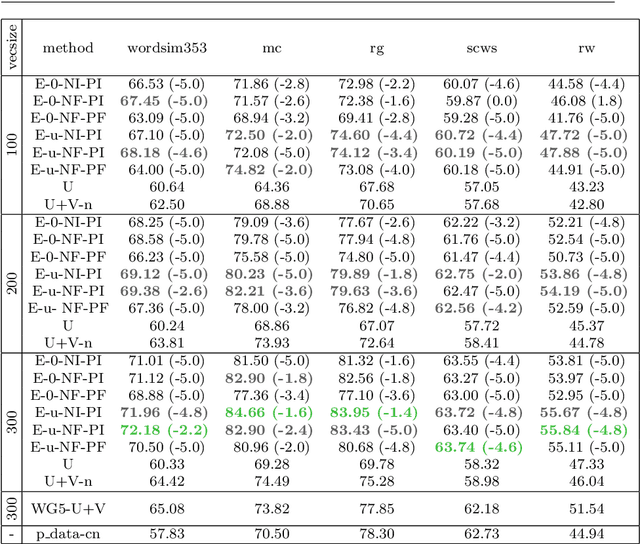
Learning an embedding for a large collection of items is a popular approach to overcome the computational limitations associated to one-hot encodings. The aim of item embedding is to learn a low dimensional space for the representations, able to capture with its geometry relevant features or relationships for the data at hand. This can be achieved for example by exploiting adjacencies among items in large sets of unlabelled data. In this paper we interpret in an Information Geometric framework the item embeddings obtained from conditional models. By exploiting the $\alpha$-geometry of the exponential family, first introduced by Amari, we introduce a family of natural $\alpha$-embeddings represented by vectors in the tangent space of the probability simplex, which includes as a special case standard approaches available in the literature. A typical example is given by word embeddings, commonly used in natural language processing, such as Word2Vec and GloVe. In our analysis, we show how the $\alpha$-deformation parameter can impact on standard evaluation tasks.

Parameters Estimation for the Cosmic Microwave Background with Bayesian Neural Networks

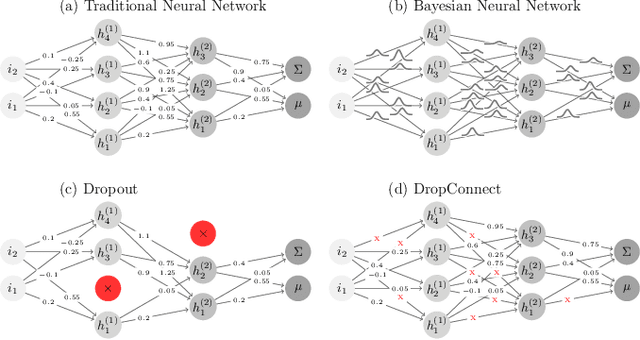
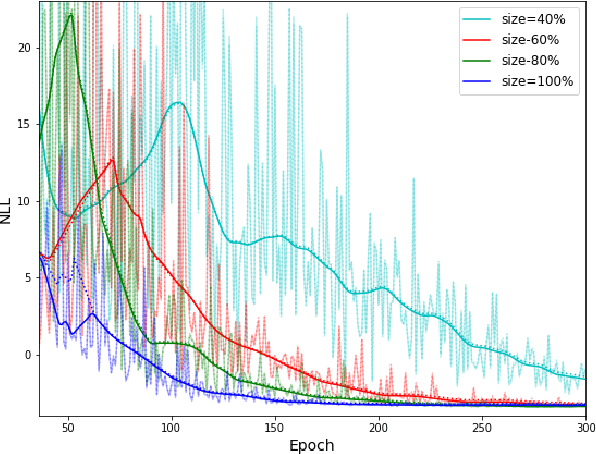
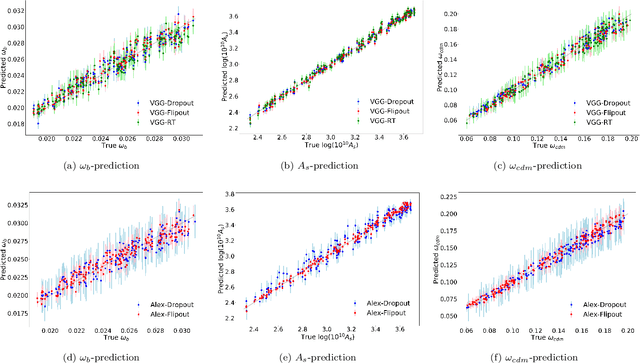
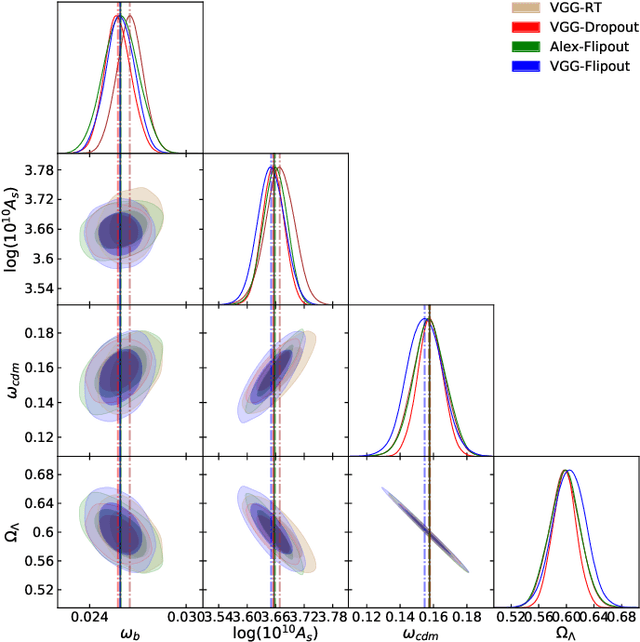
In this paper, we present the first study that compares different models of Bayesian Neural Networks (BNNs) to predict the posterior distribution of the cosmological parameters directly from the Cosmic Microwave Background temperature and polarization maps. We focus our analysis on four different methods to sample the weights of the network during training: Dropout, DropConnect, Reparameterization Trick (RT), and Flipout. We find out that Flipout outperforms all other methods regardless of the architecture used, and provides tighter constraints for the cosmological parameters. Additionally, we describe existing strategies for calibrating the networks and propose new ones. We show how tuning the regularization parameter for the scale of the approximate posterior on the weights in Flipout and RT we can produce unbiased and reliable uncertainty estimates, i.e., the regularizer acts as a hyper parameter analogous to the dropout rate in Dropout. The best performances are nevertheless achieved with a more convenient method, in which the network parameters are let free during training to achieve the best uncalibrated performances, and then the confidence intervals are calibrated in a subsequent phase. Furthermore, we claim that the correct calibration of these networks does not change the behavior for the aleatoric and epistemic uncertainties provided for BNNs when the size of the training dataset changes. The results reported in the paper can be extended to other cosmological datasets in order to capture features that can be extracted directly from the raw data, such as non-Gaussianity or foreground emissions.

Learning in Variational Autoencoders with Kullback-Leibler and Renyi Integral Bounds

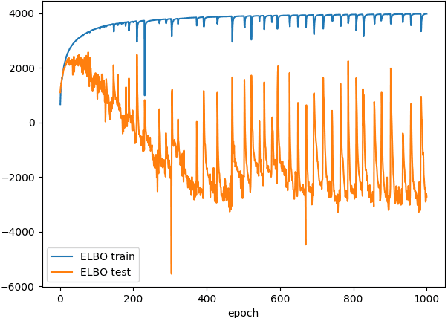
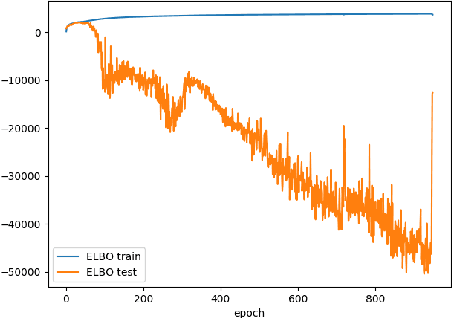
In this paper we propose two novel bounds for the log-likelihood based on Kullback-Leibler and the R\'{e}nyi divergences, which can be used for variational inference and in particular for the training of Variational AutoEncoders. Our proposal is motivated by the difficulties encountered in training VAEs on continuous datasets with high contrast images, such as those with handwritten digits and characters, where numerical issues often appear unless noise is added, either to the dataset during training or to the generative model given by the decoder. The new bounds we propose, which are obtained from the maximization of the likelihood of an interval for the observations, allow numerically stable training procedures without the necessity of adding any extra source of noise to the data.