Learning in Variational Autoencoders with Kullback-Leibler and Renyi Integral Bounds
Paper and Code
Jul 05, 2018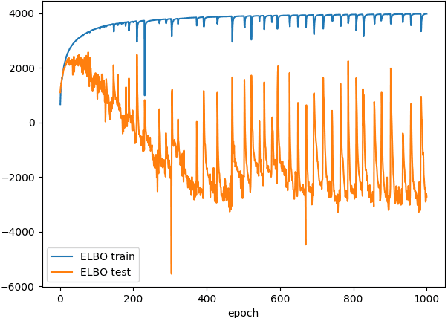
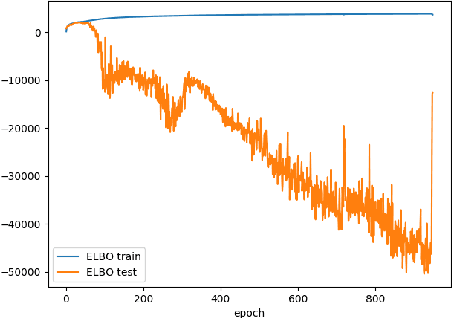
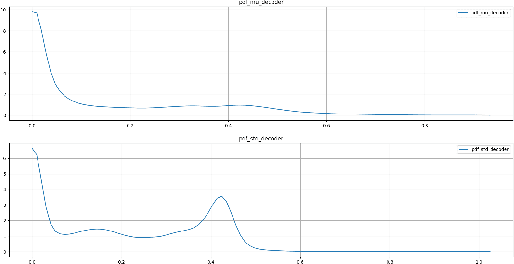

In this paper we propose two novel bounds for the log-likelihood based on Kullback-Leibler and the R\'{e}nyi divergences, which can be used for variational inference and in particular for the training of Variational AutoEncoders. Our proposal is motivated by the difficulties encountered in training VAEs on continuous datasets with high contrast images, such as those with handwritten digits and characters, where numerical issues often appear unless noise is added, either to the dataset during training or to the generative model given by the decoder. The new bounds we propose, which are obtained from the maximization of the likelihood of an interval for the observations, allow numerically stable training procedures without the necessity of adding any extra source of noise to the data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge