Natural Alpha Embeddings
Paper and Code
Dec 24, 2019
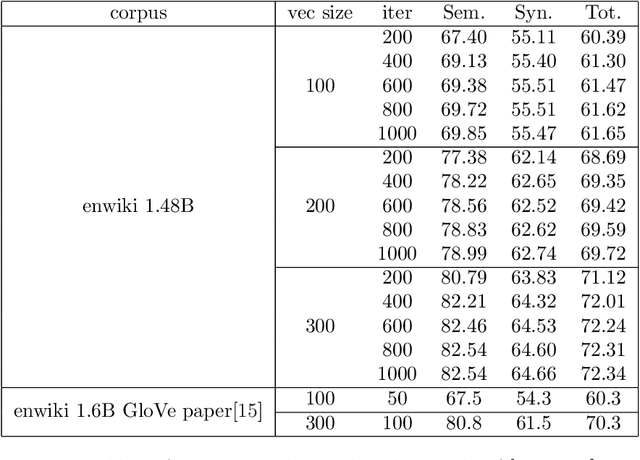
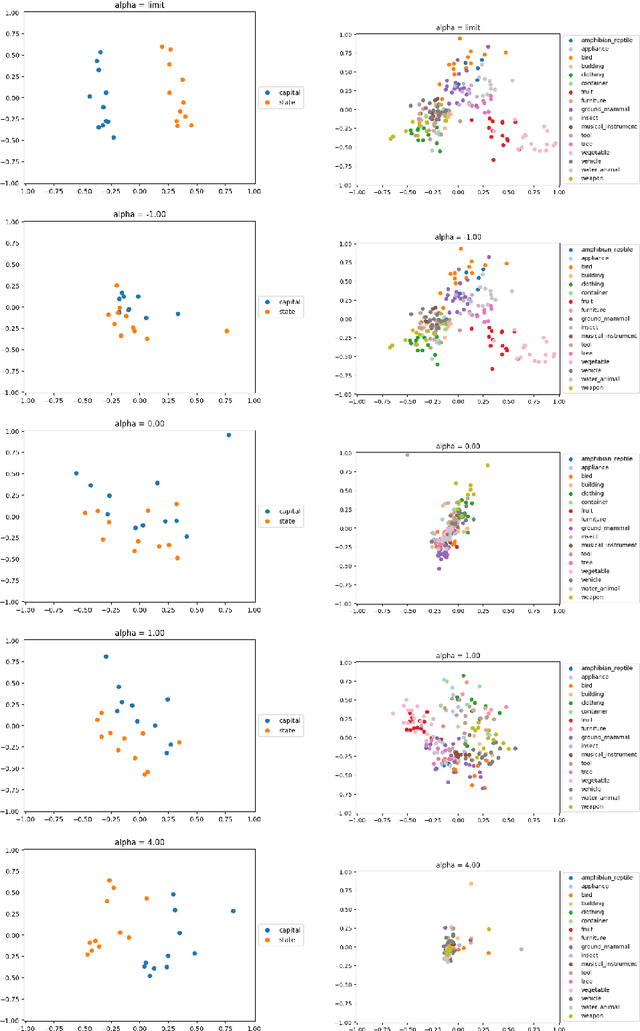
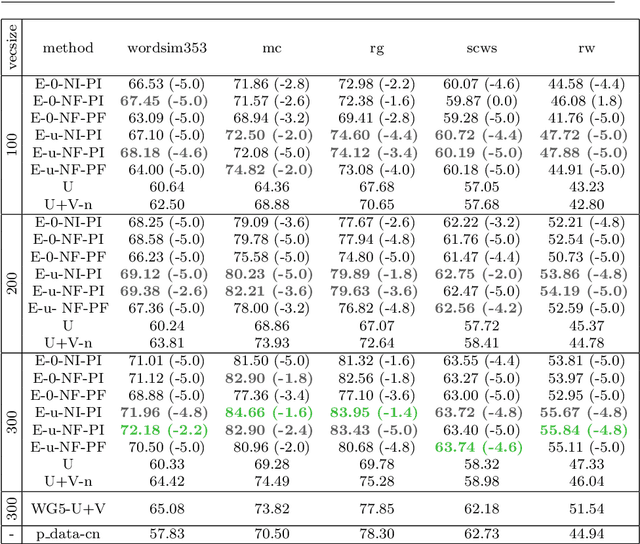
Learning an embedding for a large collection of items is a popular approach to overcome the computational limitations associated to one-hot encodings. The aim of item embedding is to learn a low dimensional space for the representations, able to capture with its geometry relevant features or relationships for the data at hand. This can be achieved for example by exploiting adjacencies among items in large sets of unlabelled data. In this paper we interpret in an Information Geometric framework the item embeddings obtained from conditional models. By exploiting the $\alpha$-geometry of the exponential family, first introduced by Amari, we introduce a family of natural $\alpha$-embeddings represented by vectors in the tangent space of the probability simplex, which includes as a special case standard approaches available in the literature. A typical example is given by word embeddings, commonly used in natural language processing, such as Word2Vec and GloVe. In our analysis, we show how the $\alpha$-deformation parameter can impact on standard evaluation tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge