Dimitri Marinelli
Accelerating MCMC algorithms through Bayesian Deep Networks
Nov 29, 2020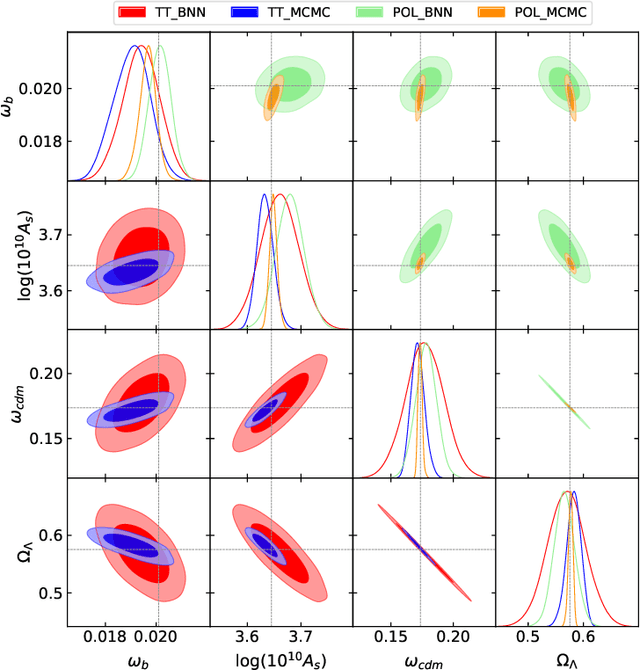
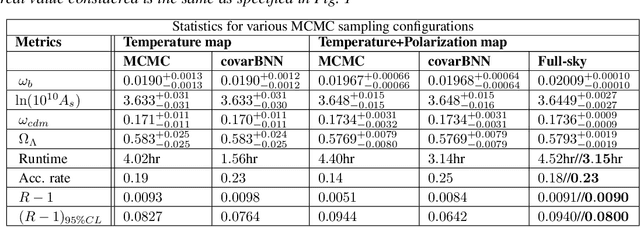
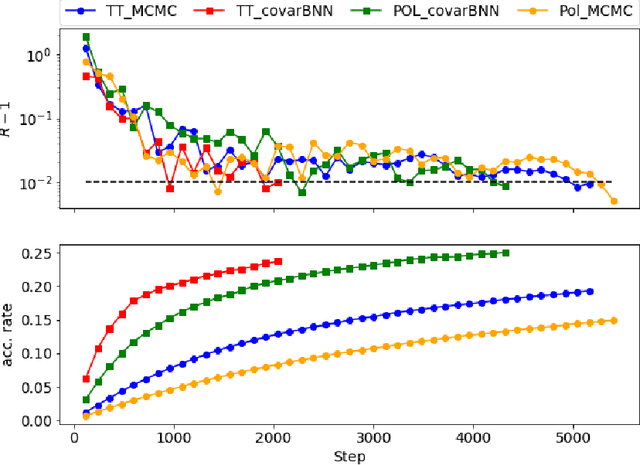
Abstract:Markov Chain Monte Carlo (MCMC) algorithms are commonly used for their versatility in sampling from complicated probability distributions. However, as the dimension of the distribution gets larger, the computational costs for a satisfactory exploration of the sampling space become challenging. Adaptive MCMC methods employing a choice of proposal distribution can address this issue speeding up the convergence. In this paper we show an alternative way of performing adaptive MCMC, by using the outcome of Bayesian Neural Networks as the initial proposal for the Markov Chain. This combined approach increases the acceptance rate in the Metropolis-Hasting algorithm and accelerate the convergence of the MCMC while reaching the same final accuracy. Finally, we demonstrate the main advantages of this approach by constraining the cosmological parameters directly from Cosmic Microwave Background maps.
Parameters Estimation for the Cosmic Microwave Background with Bayesian Neural Networks
Dec 23, 2019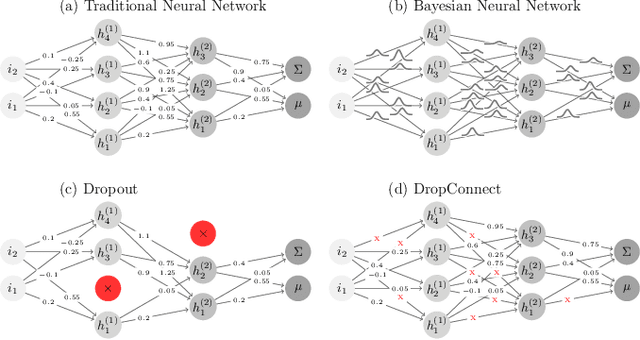
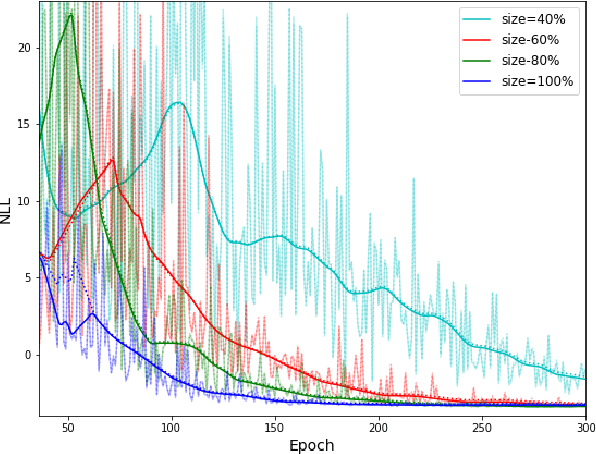
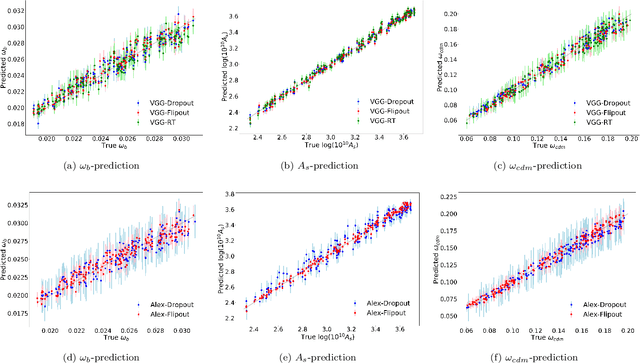
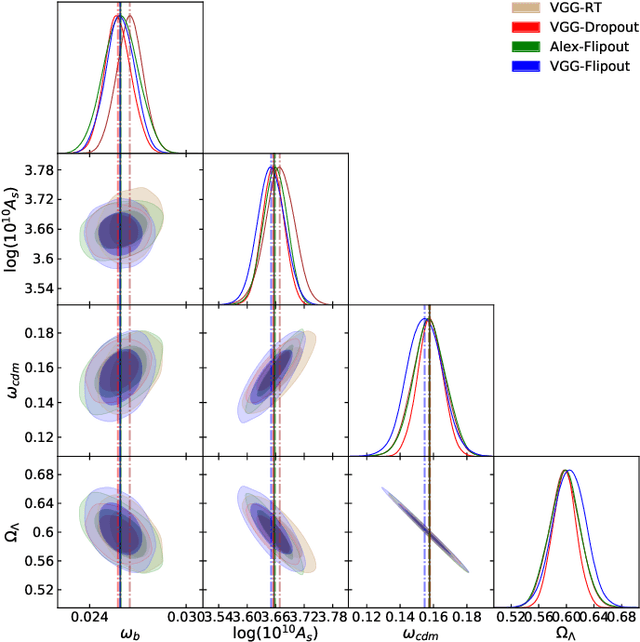
Abstract:In this paper, we present the first study that compares different models of Bayesian Neural Networks (BNNs) to predict the posterior distribution of the cosmological parameters directly from the Cosmic Microwave Background temperature and polarization maps. We focus our analysis on four different methods to sample the weights of the network during training: Dropout, DropConnect, Reparameterization Trick (RT), and Flipout. We find out that Flipout outperforms all other methods regardless of the architecture used, and provides tighter constraints for the cosmological parameters. Additionally, we describe existing strategies for calibrating the networks and propose new ones. We show how tuning the regularization parameter for the scale of the approximate posterior on the weights in Flipout and RT we can produce unbiased and reliable uncertainty estimates, i.e., the regularizer acts as a hyper parameter analogous to the dropout rate in Dropout. The best performances are nevertheless achieved with a more convenient method, in which the network parameters are let free during training to achieve the best uncalibrated performances, and then the confidence intervals are calibrated in a subsequent phase. Furthermore, we claim that the correct calibration of these networks does not change the behavior for the aleatoric and epistemic uncertainties provided for BNNs when the size of the training dataset changes. The results reported in the paper can be extended to other cosmological datasets in order to capture features that can be extracted directly from the raw data, such as non-Gaussianity or foreground emissions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge