Embedding Safety into RL: A New Take on Trust Region Methods

Reinforcement Learning (RL) agents are able to solve a wide variety of tasks but are prone to producing unsafe behaviors. Constrained Markov Decision Processes (CMDPs) provide a popular framework for incorporating safety constraints. However, common solution methods often compromise reward maximization by being overly conservative or allow unsafe behavior during training. We propose Constrained Trust Region Policy Optimization (C-TRPO), a novel approach that modifies the geometry of the policy space based on the safety constraints and yields trust regions composed exclusively of safe policies, ensuring constraint satisfaction throughout training. We theoretically study the convergence and update properties of C-TRPO and highlight connections to TRPO, Natural Policy Gradient (NPG), and Constrained Policy Optimization (CPO). Finally, we demonstrate experimentally that C-TRPO significantly reduces constraint violations while achieving competitive reward maximization compared to state-of-the-art CMDP algorithms.

Dynamical Measure Transport and Neural PDE Solvers for Sampling

The task of sampling from a probability density can be approached as transporting a tractable density function to the target, known as dynamical measure transport. In this work, we tackle it through a principled unified framework using deterministic or stochastic evolutions described by partial differential equations (PDEs). This framework incorporates prior trajectory-based sampling methods, such as diffusion models or Schr\"odinger bridges, without relying on the concept of time-reversals. Moreover, it allows us to propose novel numerical methods for solving the transport task and thus sampling from complicated targets without the need for the normalization constant or data samples. We employ physics-informed neural networks (PINNs) to approximate the respective PDE solutions, implying both conceptional and computational advantages. In particular, PINNs allow for simulation- and discretization-free optimization and can be trained very efficiently, leading to significantly better mode coverage in the sampling task compared to alternative methods. Moreover, they can readily be fine-tuned with Gauss-Newton methods to achieve high accuracy in sampling.

Essentially Sharp Estimates on the Entropy Regularization Error in Discrete Discounted Markov Decision Processes

We study the error introduced by entropy regularization of infinite-horizon discrete discounted Markov decision processes. We show that this error decreases exponentially in the inverse regularization strength both in a weighted KL-divergence and in value with a problem-specific exponent. We provide a lower bound matching our upper bound up to a polynomial factor. Our proof relies on the correspondence of the solutions of entropy-regularized Markov decision processes with gradient flows of the unregularized reward with respect to a Riemannian metric common in natural policy gradient methods. Further, this correspondence allows us to identify the limit of the gradient flow as the generalized maximum entropy optimal policy, thereby characterizing the implicit bias of the Kakade gradient flow which corresponds to a time-continuous version of the natural policy gradient method. We use this to show that for entropy-regularized natural policy gradient methods the overall error decays exponentially in the square root of the number of iterations improving existing sublinear guarantees.

Fisher-Rao Gradient Flows of Linear Programs and State-Action Natural Policy Gradients

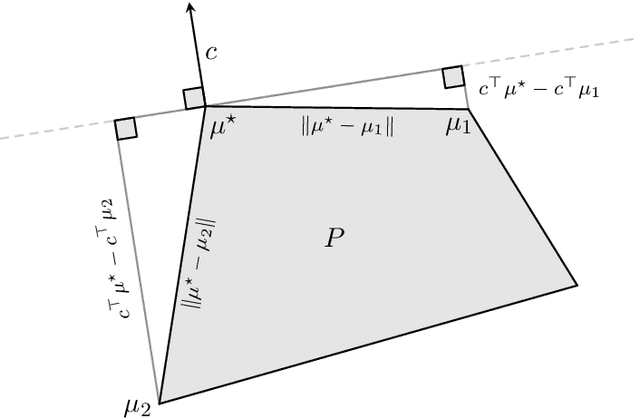
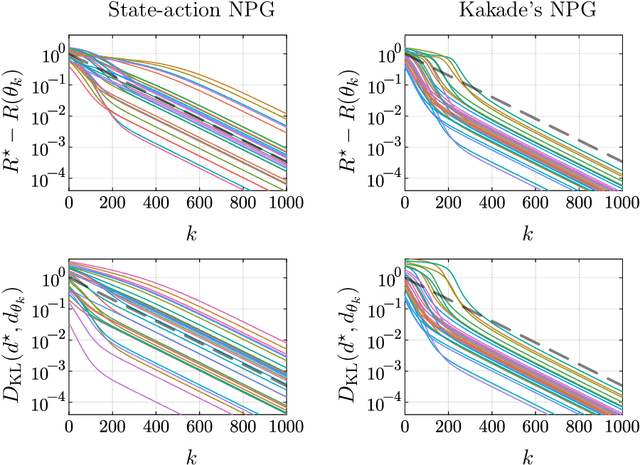
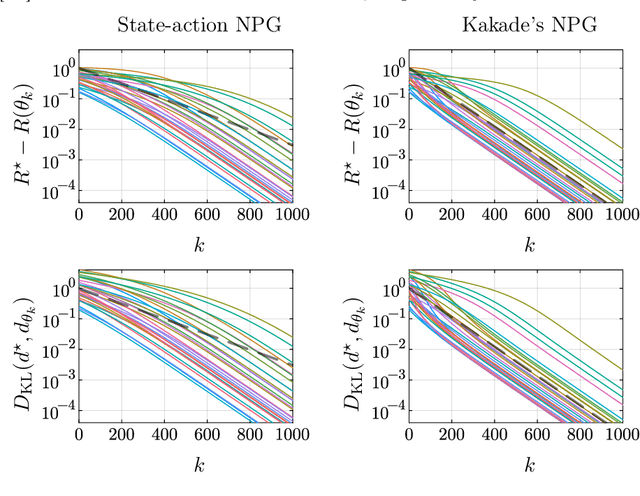
Kakade's natural policy gradient method has been studied extensively in the last years showing linear convergence with and without regularization. We study another natural gradient method which is based on the Fisher information matrix of the state-action distributions and has received little attention from the theoretical side. Here, the state-action distributions follow the Fisher-Rao gradient flow inside the state-action polytope with respect to a linear potential. Therefore, we study Fisher-Rao gradient flows of linear programs more generally and show linear convergence with a rate that depends on the geometry of the linear program. Equivalently, this yields an estimate on the error induced by entropic regularization of the linear program which improves existing results. We extend these results and show sublinear convergence for perturbed Fisher-Rao gradient flows and natural gradient flows up to an approximation error. In particular, these general results cover the case of state-action natural policy gradients.

Achieving High Accuracy with PINNs via Energy Natural Gradients

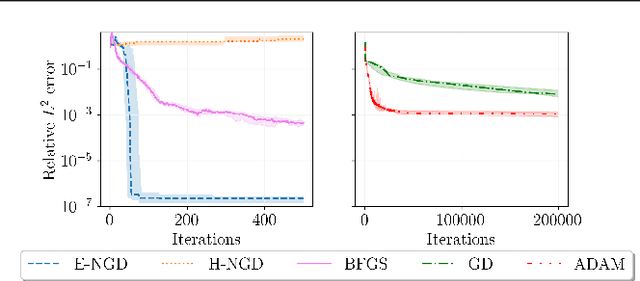
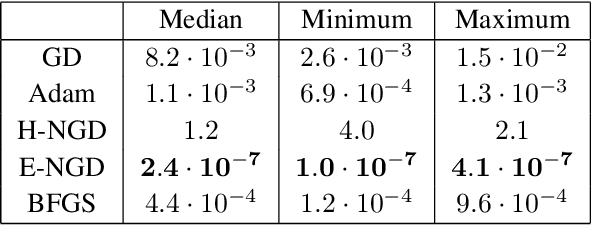
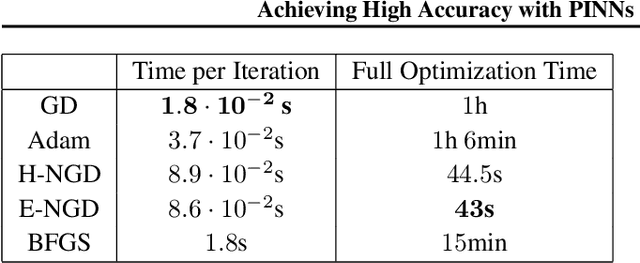
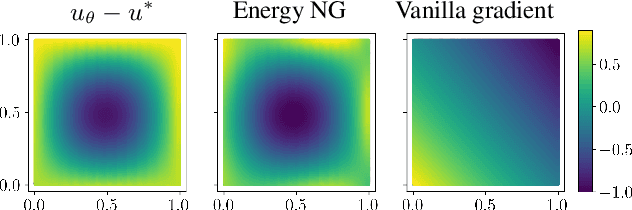
We propose energy natural gradient descent, a natural gradient method with respect to a Hessian-induced Riemannian metric as an optimization algorithm for physics-informed neural networks (PINNs) and the deep Ritz method. As a main motivation we show that the update direction in function space resulting from the energy natural gradient corresponds to the Newton direction modulo an orthogonal projection onto the model's tangent space. We demonstrate experimentally that energy natural gradient descent yields highly accurate solutions with errors several orders of magnitude smaller than what is obtained when training PINNs with standard optimizers like gradient descent or Adam, even when those are allowed significantly more computation time.

Geometry and convergence of natural policy gradient methods

We study the convergence of several natural policy gradient (NPG) methods in infinite-horizon discounted Markov decision processes with regular policy parametrizations. For a variety of NPGs and reward functions we show that the trajectories in state-action space are solutions of gradient flows with respect to Hessian geometries, based on which we obtain global convergence guarantees and convergence rates. In particular, we show linear convergence for unregularized and regularized NPG flows with the metrics proposed by Kakade and Morimura and co-authors by observing that these arise from the Hessian geometries of conditional entropy and entropy respectively. Further, we obtain sublinear convergence rates for Hessian geometries arising from other convex functions like log-barriers. Finally, we interpret the discrete-time NPG methods with regularized rewards as inexact Newton methods if the NPG is defined with respect to the Hessian geometry of the regularizer. This yields local quadratic convergence rates of these methods for step size equal to the penalization strength.

Extrinsic Camera Calibration with Semantic Segmentation

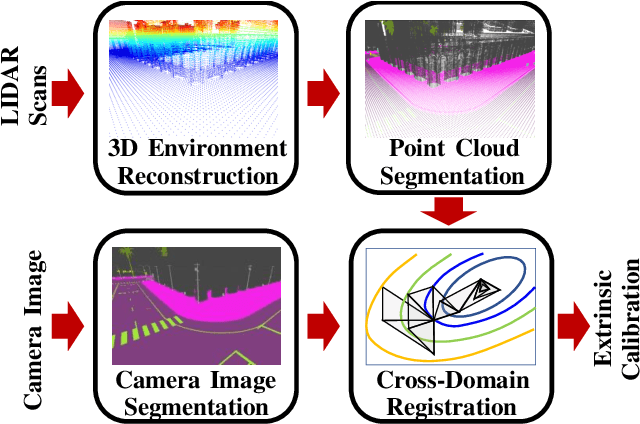
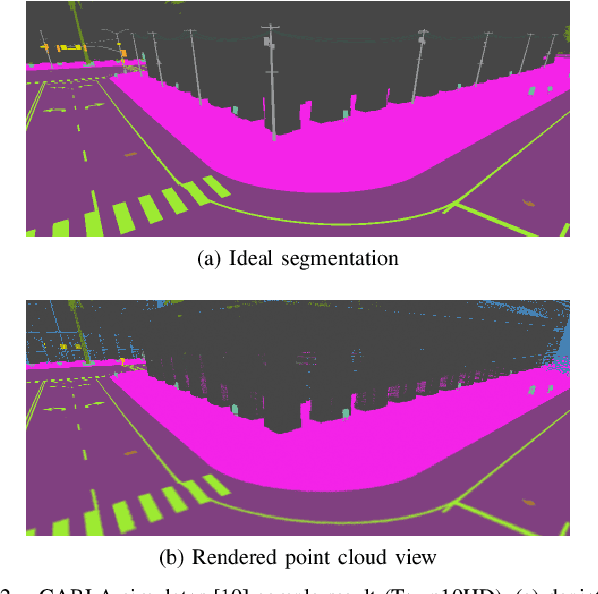
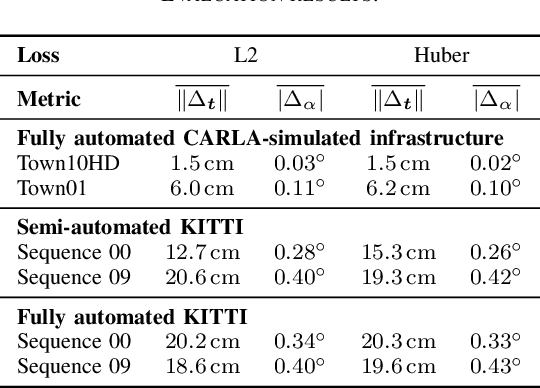
Monocular camera sensors are vital to intelligent vehicle operation and automated driving assistance and are also heavily employed in traffic control infrastructure. Calibrating the monocular camera, though, is time-consuming and often requires significant manual intervention. In this work, we present an extrinsic camera calibration approach that automatizes the parameter estimation by utilizing semantic segmentation information from images and point clouds. Our approach relies on a coarse initial measurement of the camera pose and builds on lidar sensors mounted on a vehicle with high-precision localization to capture a point cloud of the camera environment. Afterward, a mapping between the camera and world coordinate spaces is obtained by performing a lidar-to-camera registration of the semantically segmented sensor data. We evaluate our method on simulated and real-world data to demonstrate low error measurements in the calibration results. Our approach is suitable for infrastructure sensors as well as vehicle sensors, while it does not require motion of the camera platform.

Invariance Properties of the Natural Gradient in Overparametrised Systems

The natural gradient field is a vector field that lives on a model equipped with a distinguished Riemannian metric, e.g. the Fisher-Rao metric, and represents the direction of steepest ascent of an objective function on the model with respect to this metric. In practice, one tries to obtain the corresponding direction on the parameter space by multiplying the ordinary gradient by the inverse of the Gram matrix associated with the metric. We refer to this vector on the parameter space as the natural parameter gradient. In this paper we study when the pushforward of the natural parameter gradient is equal to the natural gradient. Furthermore we investigate the invariance properties of the natural parameter gradient. Both questions are addressed in an overparametrised setting.

Self-Assessment for Single-Object Tracking in Clutter Using Subjective Logic

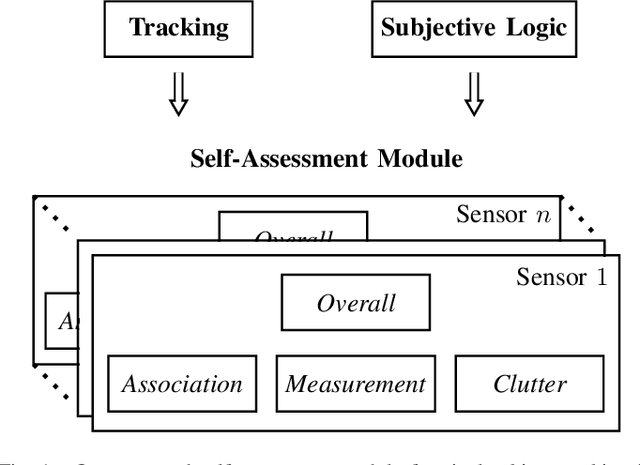
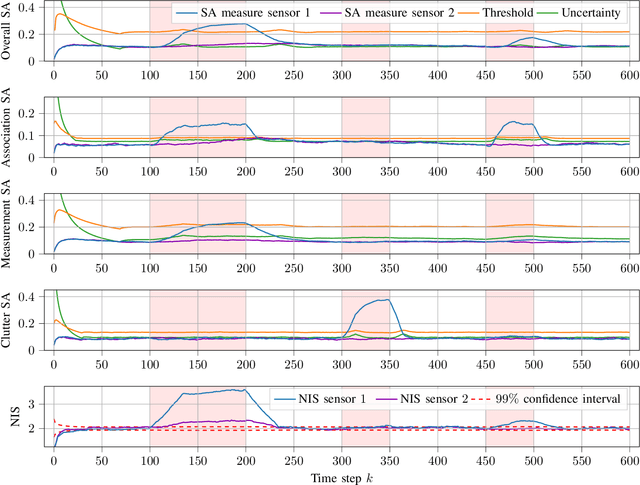
Reliable tracking algorithms are essential for automated driving. However, the existing consistency measures are not sufficient to meet the increasing safety demands in the automotive sector. Therefore, this work presents a novel method for self-assessment of single-object tracking in clutter based on Kalman filtering and subjective logic. A key feature of the approach is that it additionally provides a measure of the collected statistical evidence in its online reliability scores. In this way, various aspects of reliability, such as the correctness of the assumed measurement noise, detection probability, and clutter rate, can be monitored in addition to the overall assessment based on the available evidence. Here, we present a mathematical derivation of the reference distribution used in our self-assessment module for our studied problem. Moreover, we introduce a formula that describes how a threshold should be chosen for the degree of conflict, the subjective logic comparison measure used for the reliability decision making. Our approach is evaluated in a challenging simulation scenario designed to model adverse weather conditions. The simulations show that our method can significantly improve the reliability checking of single-object tracking in clutter in several aspects.

Solving infinite-horizon POMDPs with memoryless stochastic policies in state-action space

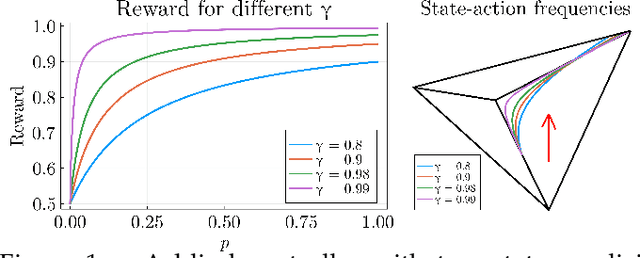
Reward optimization in fully observable Markov decision processes is equivalent to a linear program over the polytope of state-action frequencies. Taking a similar perspective in the case of partially observable Markov decision processes with memoryless stochastic policies, the problem was recently formulated as the optimization of a linear objective subject to polynomial constraints. Based on this we present an approach for Reward Optimization in State-Action space (ROSA). We test this approach experimentally in maze navigation tasks. We find that ROSA is computationally efficient and can yield stability improvements over other existing methods.