Fisher-Rao Gradient Flows of Linear Programs and State-Action Natural Policy Gradients
Paper and Code
Mar 28, 2024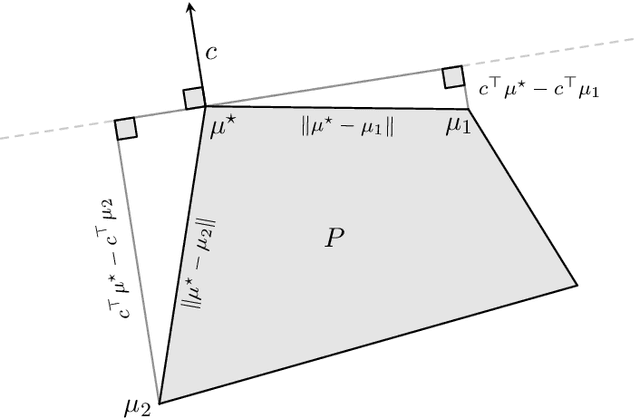
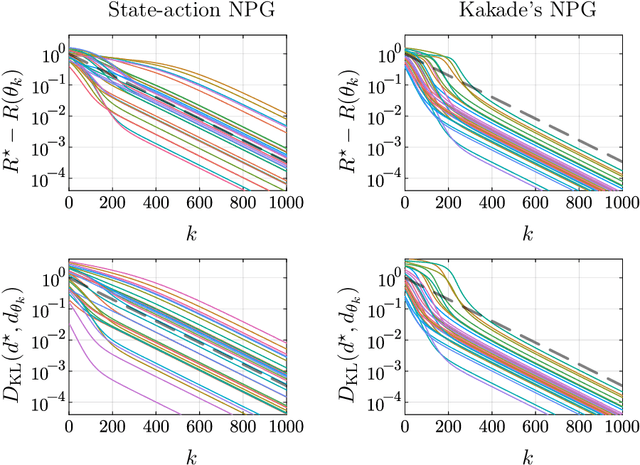
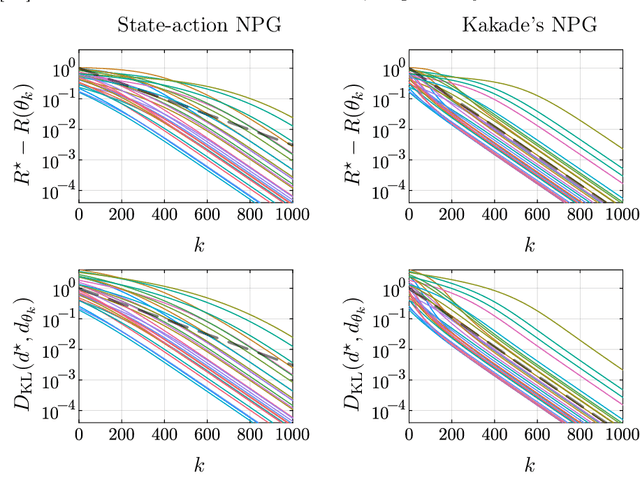
Kakade's natural policy gradient method has been studied extensively in the last years showing linear convergence with and without regularization. We study another natural gradient method which is based on the Fisher information matrix of the state-action distributions and has received little attention from the theoretical side. Here, the state-action distributions follow the Fisher-Rao gradient flow inside the state-action polytope with respect to a linear potential. Therefore, we study Fisher-Rao gradient flows of linear programs more generally and show linear convergence with a rate that depends on the geometry of the linear program. Equivalently, this yields an estimate on the error induced by entropic regularization of the linear program which improves existing results. We extend these results and show sublinear convergence for perturbed Fisher-Rao gradient flows and natural gradient flows up to an approximation error. In particular, these general results cover the case of state-action natural policy gradients.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge