Solving infinite-horizon POMDPs with memoryless stochastic policies in state-action space
Paper and Code
May 27, 2022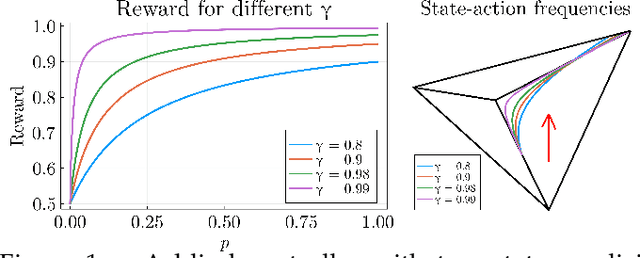

Reward optimization in fully observable Markov decision processes is equivalent to a linear program over the polytope of state-action frequencies. Taking a similar perspective in the case of partially observable Markov decision processes with memoryless stochastic policies, the problem was recently formulated as the optimization of a linear objective subject to polynomial constraints. Based on this we present an approach for Reward Optimization in State-Action space (ROSA). We test this approach experimentally in maze navigation tasks. We find that ROSA is computationally efficient and can yield stability improvements over other existing methods.
* Accepted as an extended abstract at RLDM 2022, 5 pages, 2 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge