Comparing Information-Theoretic Measures of Complexity in Boltzmann Machines

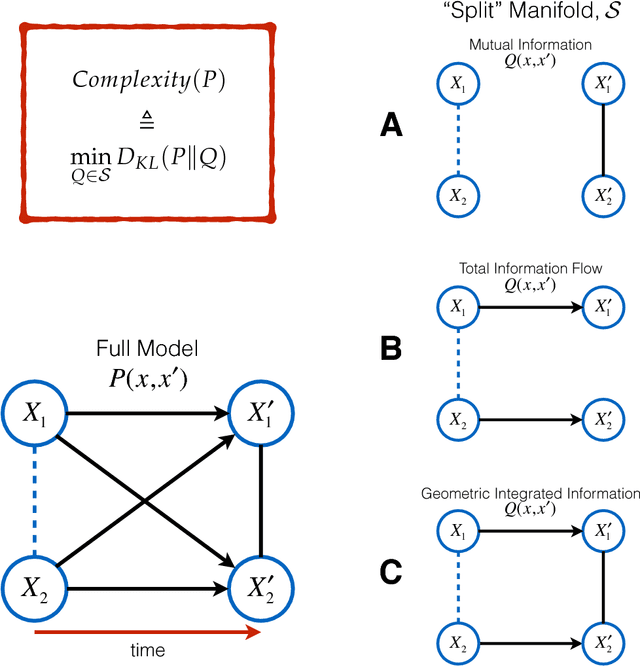
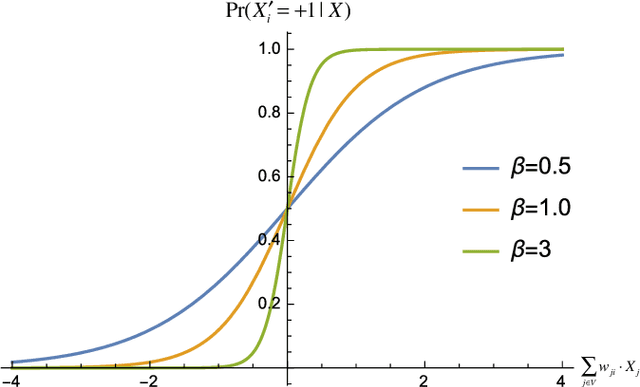
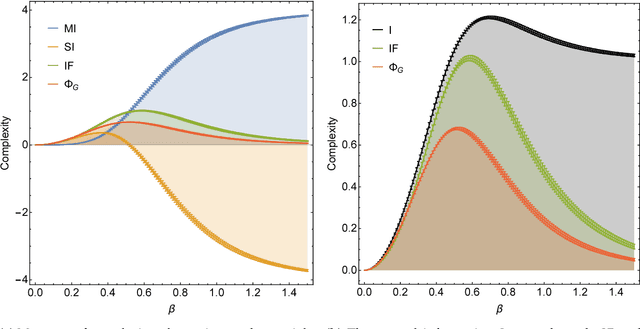
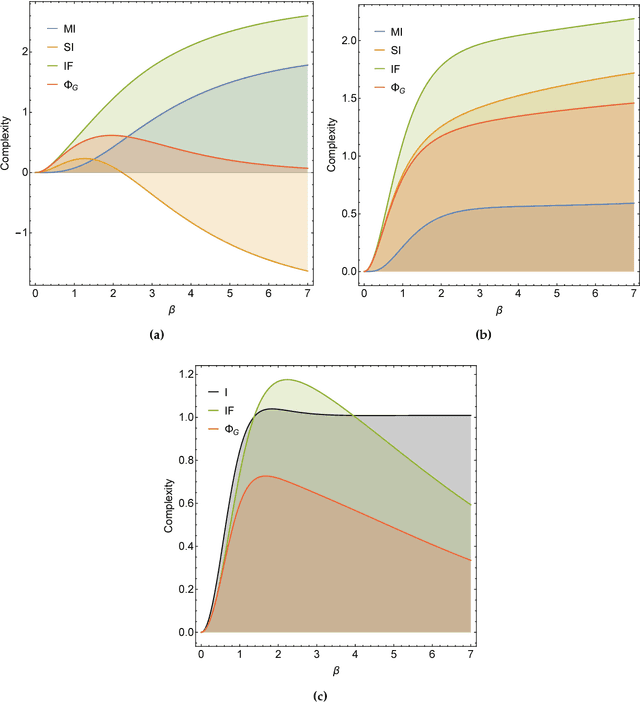
In the past three decades, many theoretical measures of complexity have been proposed to help understand complex systems. In this work, for the first time, we place these measures on a level playing field, to explore the qualitative similarities and differences between them, and their shortcomings. Specifically, using the Boltzmann machine architecture (a fully connected recurrent neural network) with uniformly distributed weights as our model of study, we numerically measure how complexity changes as a function of network dynamics and network parameters. We apply an extension of one such information-theoretic measure of complexity to understand incremental Hebbian learning in Hopfield networks, a fully recurrent architecture model of autoassociative memory. In the course of Hebbian learning, the total information flow reflects a natural upward trend in complexity as the network attempts to learn more and more patterns.

Optimal high-level descriptions of dynamical systems

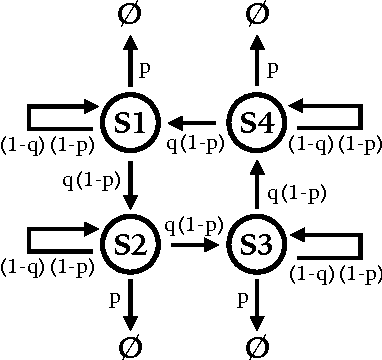
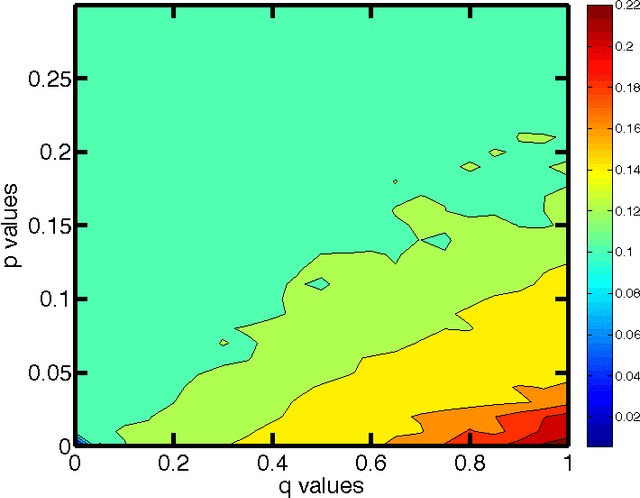
To analyze high-dimensional systems, many fields in science and engineering rely on high-level descriptions, sometimes called "macrostates," "coarse-grainings," or "effective theories". Examples of such descriptions include the thermodynamic properties of a large collection of point particles undergoing reversible dynamics, the variables in a macroeconomic model describing the individuals that participate in an economy, and the summary state of a cell composed of a large set of biochemical networks. Often these high-level descriptions are constructed without considering the ultimate reason for needing them in the first place. Here, we formalize and quantify one such purpose: the need to predict observables of interest concerning the high-dimensional system with as high accuracy as possible, while minimizing the computational cost of doing so. The resulting State Space Compression (SSC) framework provides a guide for how to solve for the {optimal} high-level description of a given dynamical system, rather than constructing it based on human intuition alone. In this preliminary report, we introduce SSC, and illustrate it with several information-theoretic quantifications of "accuracy", all with different implications for the optimal compression. We also discuss some other possible applications of SSC beyond the goal of accurate prediction. These include SSC as a measure of the complexity of a dynamical system, and as a way to quantify information flow between the scales of a system.