David H. Wolpert
What can we know about that which we cannot even imagine?
Aug 08, 2022Abstract:In this essay I will consider a sequence of questions, ending with one about the breadth and depth of the epistemic limitations of our our science and mathematics. I will then suggest a possible way to circumvent such limitations. I begin by considering questions about the biological function of intelligence. This will lead into questions concerning human language, perhaps the most important cognitive prosthesis we have ever developed. While it is traditional to rhapsodize about the perceptual power provided by human language, I will emphasize how horribly limited - and therefore limiting - it is. This will lead to questions of whether human mathematics, being so deeply grounded in our language, is also deeply limited. I will then combine all of this into a partial, sort-of, sideways answer to the guiding question of this essay: what we can ever discern about all that we cannot even conceive of?
The Past as a Stochastic Process
Dec 11, 2021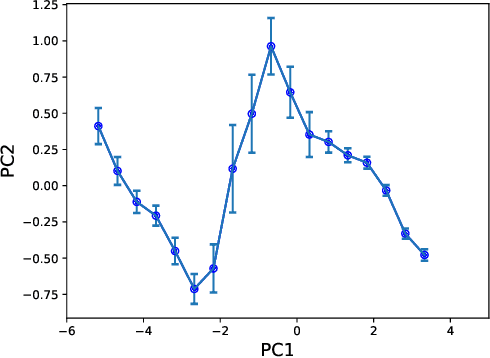
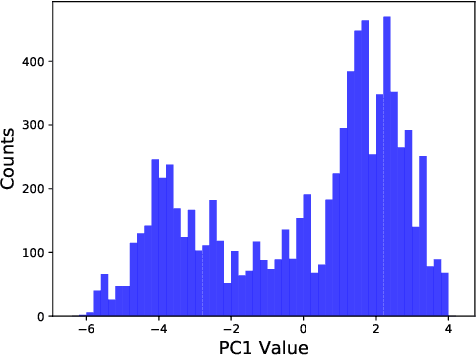
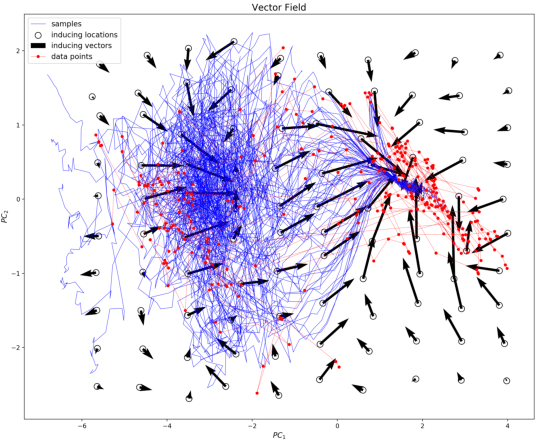
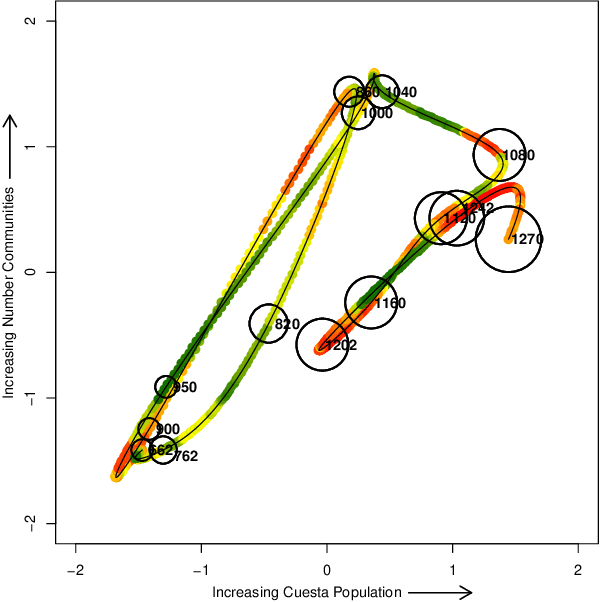
Abstract:Historical processes manifest remarkable diversity. Nevertheless, scholars have long attempted to identify patterns and categorize historical actors and influences with some success. A stochastic process framework provides a structured approach for the analysis of large historical datasets that allows for detection of sometimes surprising patterns, identification of relevant causal actors both endogenous and exogenous to the process, and comparison between different historical cases. The combination of data, analytical tools and the organizing theoretical framework of stochastic processes complements traditional narrative approaches in history and archaeology.
The Implications of the No-Free-Lunch Theorems for Meta-induction
Mar 22, 2021Abstract:The important recent book by G. Schurz appreciates that the no-free-lunch theorems (NFL) have major implications for the problem of (meta) induction. Here I review the NFL theorems, emphasizing that they do not only concern the case where there is a uniform prior -- they prove that there are ``as many priors'' (loosely speaking) for which any induction algorithm $A$ out-generalizes some induction algorithm $B$ as vice-versa. Importantly though, in addition to the NFL theorems, there are many \textit{free lunch} theorems. In particular, the NFL theorems can only be used to compare the \textit{marginal} expected performance of an induction algorithm $A$ with the marginal expected performance of an induction algorithm $B$. There is a rich set of free lunches which instead concern the statistical correlations among the generalization errors of induction algorithms. As I describe, the meta-induction algorithms that Schurz advocate as a ``solution to Hume's problem'' are just an example of such a free lunch based on correlations among the generalization errors of induction algorithms. I end by pointing out that the prior that Schurz advocates, which is uniform over bit frequencies rather than bit patterns, is contradicted by thousands of experiments in statistical physics and by the great success of the maximum entropy procedure in inductive inference.
What is important about the No Free Lunch theorems?
Jul 21, 2020Abstract:The No Free Lunch theorems prove that under a uniform distribution over induction problems (search problems or learning problems), all induction algorithms perform equally. As I discuss in this chapter, the importance of the theorems arises by using them to analyze scenarios involving {non-uniform} distributions, and to compare different algorithms, without any assumption about the distribution over problems at all. In particular, the theorems prove that {anti}-cross-validation (choosing among a set of candidate algorithms based on which has {worst} out-of-sample behavior) performs as well as cross-validation, unless one makes an assumption -- which has never been formalized -- about how the distribution over induction problems, on the one hand, is related to the set of algorithms one is choosing among using (anti-)cross validation, on the other. In addition, they establish strong caveats concerning the significance of the many results in the literature which establish the strength of a particular algorithm without assuming a particular distribution. They also motivate a ``dictionary'' between supervised learning and improve blackbox optimization, which allows one to ``translate'' techniques from supervised learning into the domain of blackbox optimization, thereby strengthening blackbox optimization algorithms. In addition to these topics, I also briefly discuss their implications for philosophy of science.
Uncertainty relations and fluctuation theorems for Bayes nets
Nov 07, 2019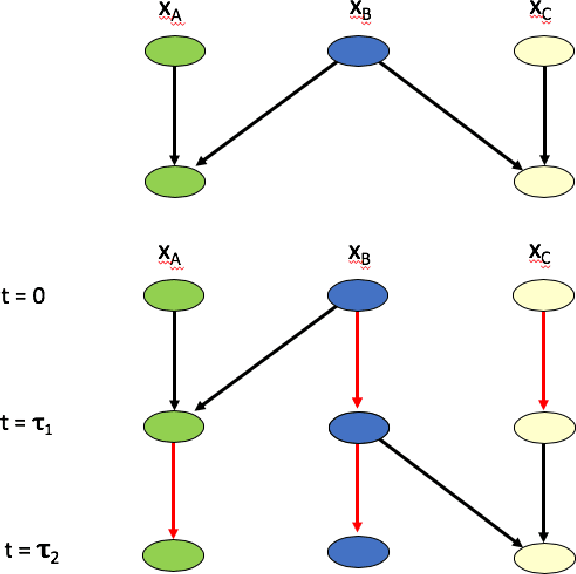
Abstract:The pioneering paper [Ito and Sagawa, 2013] analyzed the non-equilibrium statistical physics of a set of multiple interacting systems, S, whose joint discrete-time evolution is specified by a Bayesian network. The major result of [Ito and Sagawa, 2013] was an integral fluctuation theorem (IFT) governing the sum of two quantities: the entropy production (EP) of an arbitrary single v in S, and the transfer entropy from v to the other systems. Here I extend the analysis in [Ito and Sagawa, 2013]. I derive several detailed fluctuation theorems (DFTs), concerning arbitrary subsets of all the systems (including the full set). I also derive several associated IFTs, concerning an arbitrary subset of the systems, thereby extending the IFT in [Ito and Sagawa, 2013]. In addition I derive "conditional" DFTs and IFTs, involving conditional probability distributions rather than (as in conventional fluctuation theorems) unconditioned distributions. I then derive thermodynamic uncertainty relations relating the total EP of the Bayes net to the set of all the precisions of probability currents within the individual systems. I end with an example of that uncertainty relation.
Nonlinear Information Bottleneck
Sep 04, 2018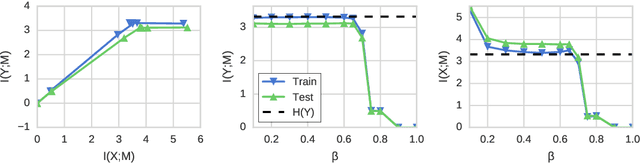
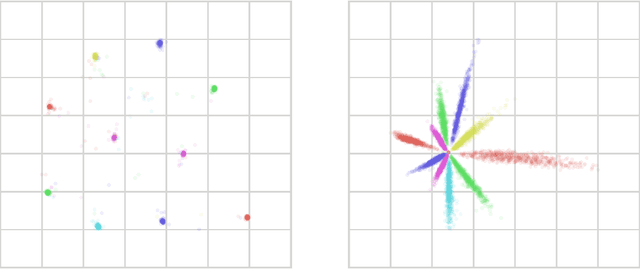
Abstract:Information bottleneck [IB] is a technique for extracting information in some `input' random variable that is relevant for predicting some different 'output' random variable. IB works by encoding the input in a compressed 'bottleneck variable' from which the output can then be accurately decoded. IB can be difficult to compute in practice, and has been mainly developed for two limited cases: (1) discrete random variables with small state spaces, and (2) continuous random variables that are jointly Gaussian distributed (in which case the encoding and decoding maps are linear). We propose a method to perform IB in more general domains. Our approach can be applied to discrete or continuous inputs and outputs, and allows for nonlinear encoding and decoding maps. The method uses a novel upper bound on the IB objective, derived using a non-parametric estimator of mutual information and a variational approximation. We show how to implement the method using neural networks and gradient-based optimization, and demonstrate its performance on the MNIST dataset.
Upgrading from Gaussian Processes to Student's-T Processes
Jan 18, 2018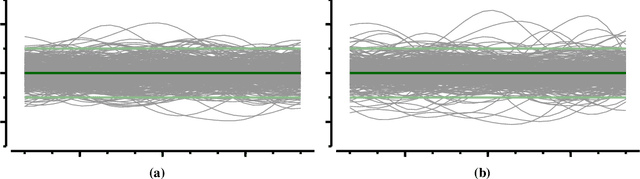
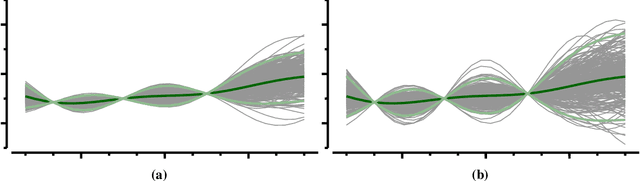
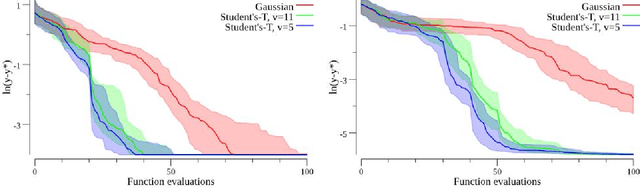
Abstract:Gaussian process priors are commonly used in aerospace design for performing Bayesian optimization. Nonetheless, Gaussian processes suffer two significant drawbacks: outliers are a priori assumed unlikely, and the posterior variance conditioned on observed data depends only on the locations of those data, not the associated sample values. Student's-T processes are a generalization of Gaussian processes, founded on the Student's-T distribution instead of the Gaussian distribution. Student's-T processes maintain the primary advantages of Gaussian processes (kernel function, analytic update rule) with additional benefits beyond Gaussian processes. The Student's-T distribution has higher Kurtosis than a Gaussian distribution and so outliers are much more likely, and the posterior variance increases or decreases depending on the variance of observed data sample values. Here, we describe Student's-T processes, and discuss their advantages in the context of aerospace optimization. We show how to construct a Student's-T process using a kernel function and how to update the process given new samples. We provide a clear derivation of optimization-relevant quantities such as expected improvement, and contrast with the related computations for Gaussian processes. Finally, we compare the performance of Student's-T processes against Gaussian process on canonical test problems in Bayesian optimization, and apply the Student's-T process to the optimization of an aerostructural design problem.
Reducing the error of Monte Carlo Algorithms by Learning Control Variates
Jun 07, 2016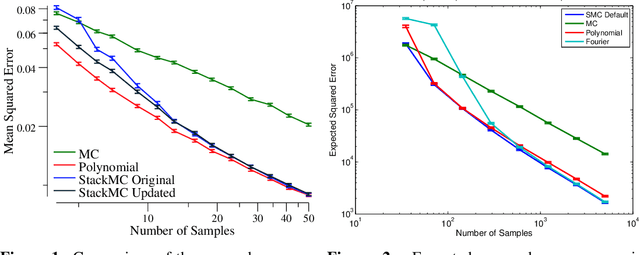
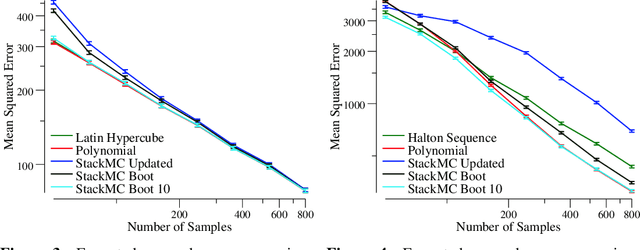
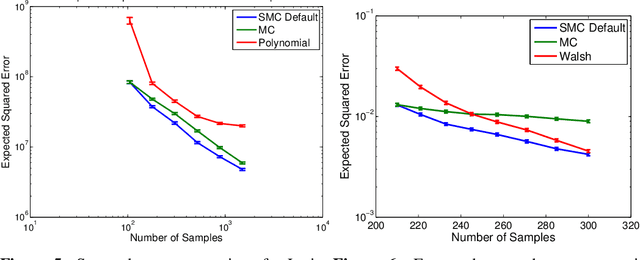
Abstract:Monte Carlo (MC) sampling algorithms are an extremely widely-used technique to estimate expectations of functions f(x), especially in high dimensions. Control variates are a very powerful technique to reduce the error of such estimates, but in their conventional form rely on having an accurate approximation of f, a priori. Stacked Monte Carlo (StackMC) is a recently introduced technique designed to overcome this limitation by fitting a control variate to the data samples themselves. Done naively, forming a control variate to the data would result in overfitting, typically worsening the MC algorithm's performance. StackMC uses in-sample / out-sample techniques to remove this overfitting. Crucially, it is a post-processing technique, requiring no additional samples, and can be applied to data generated by any MC estimator. Our preliminary experiments demonstrated that StackMC improved the estimates of expectations when it was used to post-process samples produces by a "simple sampling" MC estimator. Here we substantially extend this earlier work. We provide an in-depth analysis of the StackMC algorithm, which we use to construct an improved version of the original algorithm, with lower estimation error. We then perform experiments of StackMC on several additional kinds of MC estimators, demonstrating improved performance when the samples are generated via importance sampling, Latin-hypercube sampling and quasi-Monte Carlo sampling. We also show how to extend StackMC to combine multiple fitting functions, and how to apply it to discrete input spaces x.
Optimal high-level descriptions of dynamical systems
Jun 03, 2015
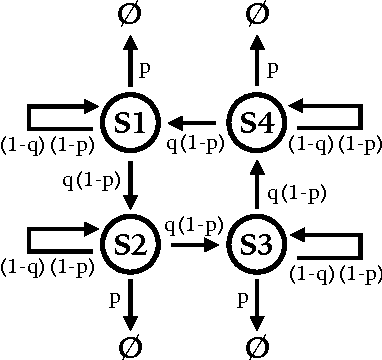
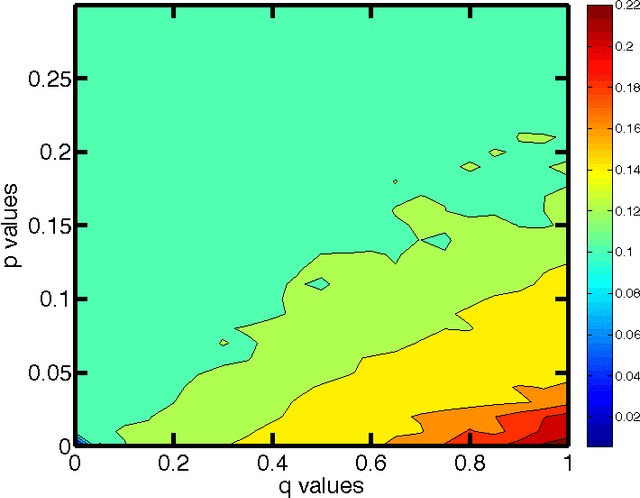

Abstract:To analyze high-dimensional systems, many fields in science and engineering rely on high-level descriptions, sometimes called "macrostates," "coarse-grainings," or "effective theories". Examples of such descriptions include the thermodynamic properties of a large collection of point particles undergoing reversible dynamics, the variables in a macroeconomic model describing the individuals that participate in an economy, and the summary state of a cell composed of a large set of biochemical networks. Often these high-level descriptions are constructed without considering the ultimate reason for needing them in the first place. Here, we formalize and quantify one such purpose: the need to predict observables of interest concerning the high-dimensional system with as high accuracy as possible, while minimizing the computational cost of doing so. The resulting State Space Compression (SSC) framework provides a guide for how to solve for the {optimal} high-level description of a given dynamical system, rather than constructing it based on human intuition alone. In this preliminary report, we introduce SSC, and illustrate it with several information-theoretic quantifications of "accuracy", all with different implications for the optimal compression. We also discuss some other possible applications of SSC beyond the goal of accurate prediction. These include SSC as a measure of the complexity of a dynamical system, and as a way to quantify information flow between the scales of a system.
Predicting the behavior of interacting humans by fusing data from multiple sources
Aug 09, 2014

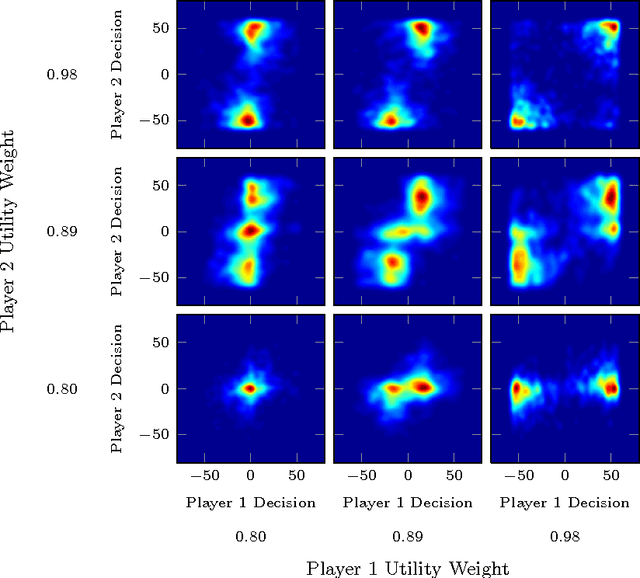

Abstract:Multi-fidelity methods combine inexpensive low-fidelity simulations with costly but highfidelity simulations to produce an accurate model of a system of interest at minimal cost. They have proven useful in modeling physical systems and have been applied to engineering problems such as wing-design optimization. During human-in-the-loop experimentation, it has become increasingly common to use online platforms, like Mechanical Turk, to run low-fidelity experiments to gather human performance data in an efficient manner. One concern with these experiments is that the results obtained from the online environment generalize poorly to the actual domain of interest. To address this limitation, we extend traditional multi-fidelity approaches to allow us to combine fewer data points from high-fidelity human-in-the-loop experiments with plentiful but less accurate data from low-fidelity experiments to produce accurate models of how humans interact. We present both model-based and model-free methods, and summarize the predictive performance of each method under dierent conditions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge