The Past as a Stochastic Process

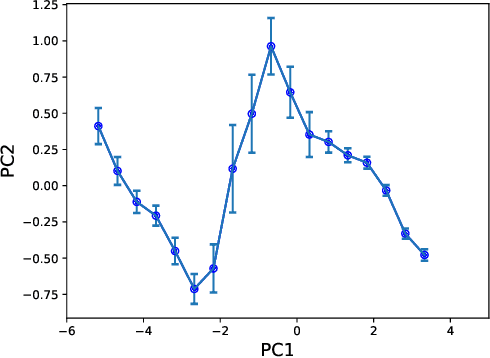
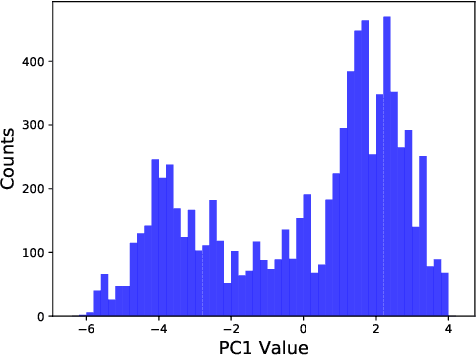
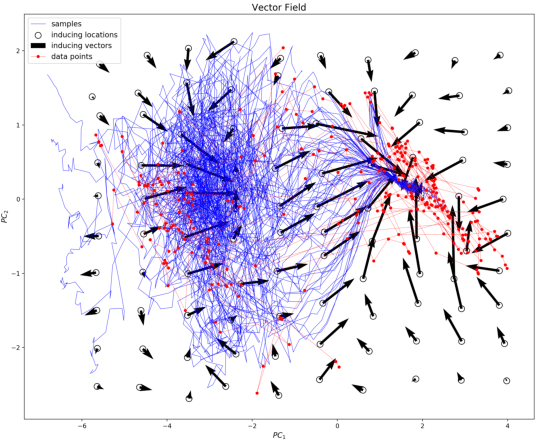
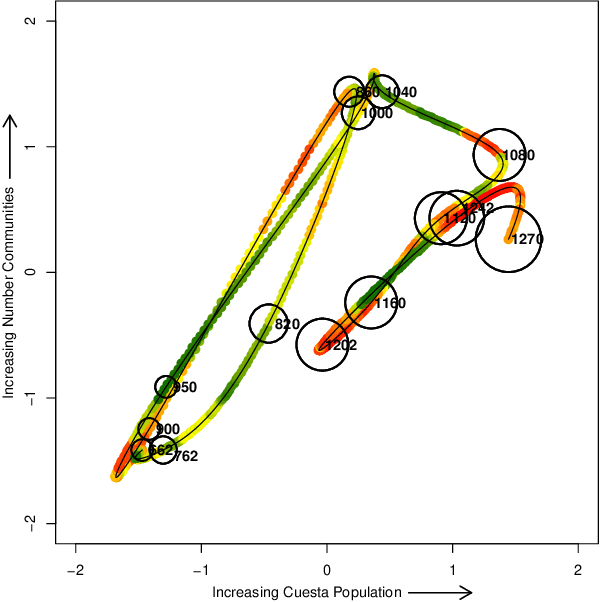
Historical processes manifest remarkable diversity. Nevertheless, scholars have long attempted to identify patterns and categorize historical actors and influences with some success. A stochastic process framework provides a structured approach for the analysis of large historical datasets that allows for detection of sometimes surprising patterns, identification of relevant causal actors both endogenous and exogenous to the process, and comparison between different historical cases. The combination of data, analytical tools and the organizing theoretical framework of stochastic processes complements traditional narrative approaches in history and archaeology.

Comparing Fairness Criteria Based on Social Outcome

Fairness in algorithmic decision-making processes is attracting increasing concern. When an algorithm is applied to human-related decision-making an estimator solely optimizing its predictive power can learn biases on the existing data, which motivates us the notion of fairness in machine learning. while several different notions are studied in the literature, little studies are done on how these notions affect the individuals. We demonstrate such a comparison between several policies induced by well-known fairness criteria, including the color-blind (CB), the demographic parity (DP), and the equalized odds (EO). We show that the EO is the only criterion among them that removes group-level disparity. Empirical studies on the social welfare and disparity of these policies are conducted.

Two-stage Algorithm for Fairness-aware Machine Learning

Algorithmic decision making process now affects many aspects of our lives. Standard tools for machine learning, such as classification and regression, are subject to the bias in data, and thus direct application of such off-the-shelf tools could lead to a specific group being unfairly discriminated. Removing sensitive attributes of data does not solve this problem because a \textit{disparate impact} can arise when non-sensitive attributes and sensitive attributes are correlated. Here, we study a fair machine learning algorithm that avoids such a disparate impact when making a decision. Inspired by the two-stage least squares method that is widely used in the field of economics, we propose a two-stage algorithm that removes bias in the training data. The proposed algorithm is conceptually simple. Unlike most of existing fair algorithms that are designed for classification tasks, the proposed method is able to (i) deal with regression tasks, (ii) combine explanatory attributes to remove reverse discrimination, and (iii) deal with numerical sensitive attributes. The performance and fairness of the proposed algorithm are evaluated in simulations with synthetic and real-world datasets.