A Generalized Framework for Multiscale State-Space Modeling with Nested Nonlinear Dynamics: An Application to Bayesian Learning under Switching Regimes

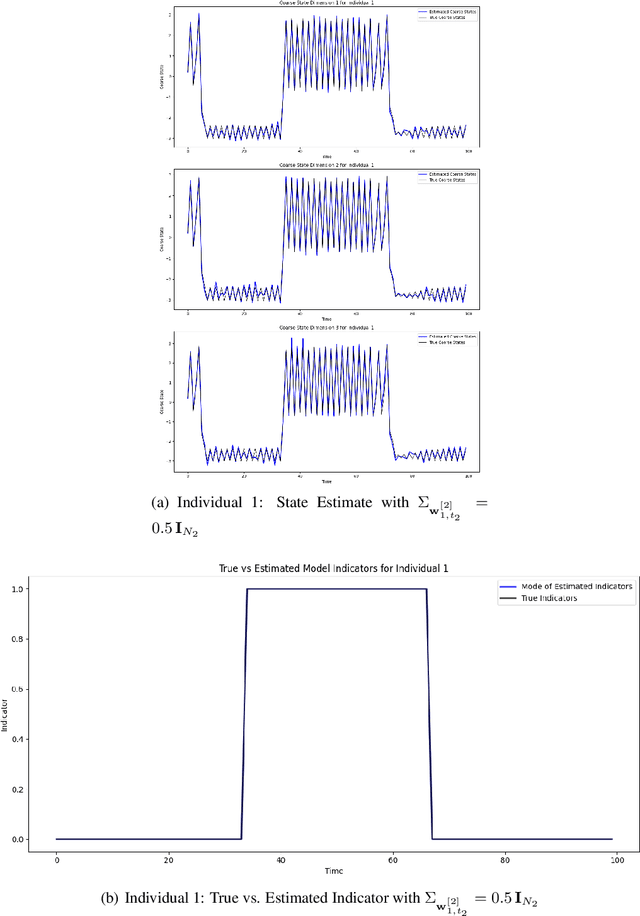
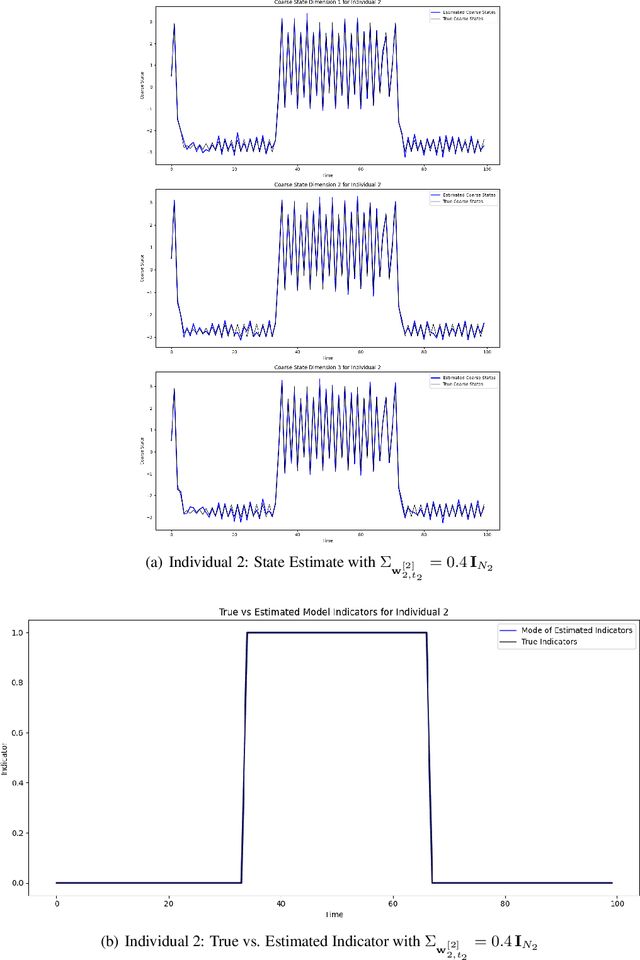
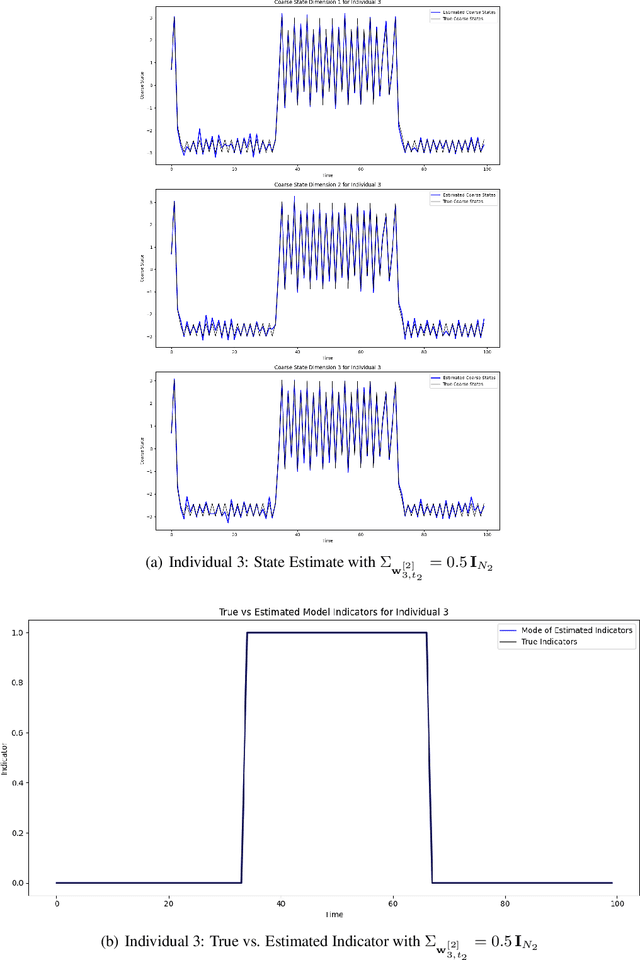
In this work, we introduce a generalized framework for multiscale state-space modeling that incorporates nested nonlinear dynamics, with a specific focus on Bayesian learning under switching regimes. Our framework captures the complex interactions between fast and slow processes within systems, allowing for the analysis of how these dynamics influence each other across various temporal scales. We model these interactions through a hierarchical structure in which finer time-scale dynamics are nested within coarser ones, while facilitating feedback between the scales. To promote the practical application of our framework, we address the problem of identifying switching regimes and transient dynamics. In particular, we develop a Bayesian learning approach to estimate latent states and indicators corresponding to switching dynamics, enabling the model to adapt effectively to regime changes. We employ Sequential Monte Carlo, or particle filtering, for inference. We illustrate the utility of our framework through simulations. The results demonstrate that our Bayesian learning approach effectively tracks state transitions and achieves accurate identification of switching dynamics in multiscale systems.

Bayesian Learning in a Nonlinear Multiscale State-Space Model

The ubiquity of multiscale interactions in complex systems is well-recognized, with development and heredity serving as a prime example of how processes at different temporal scales influence one another. This work introduces a novel multiscale state-space model to explore the dynamic interplay between systems interacting across different time scales, with feedback between each scale. We propose a Bayesian learning framework to estimate unknown states by learning the unknown process noise covariances within this multiscale model. We develop a Particle Gibbs with Ancestor Sampling (PGAS) algorithm for inference and demonstrate through simulations the efficacy of our approach.

The Past as a Stochastic Process

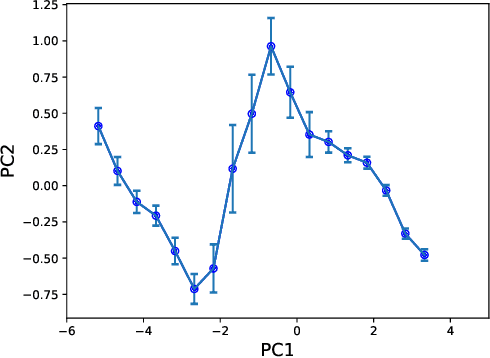
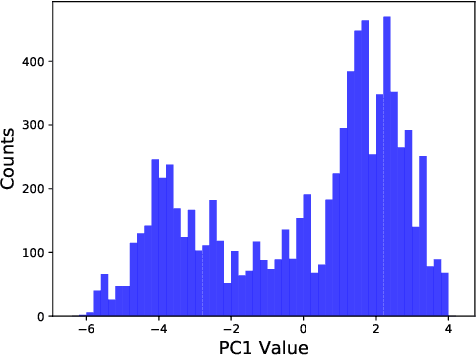
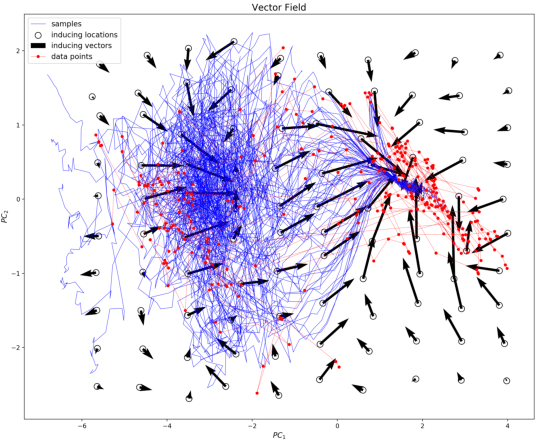
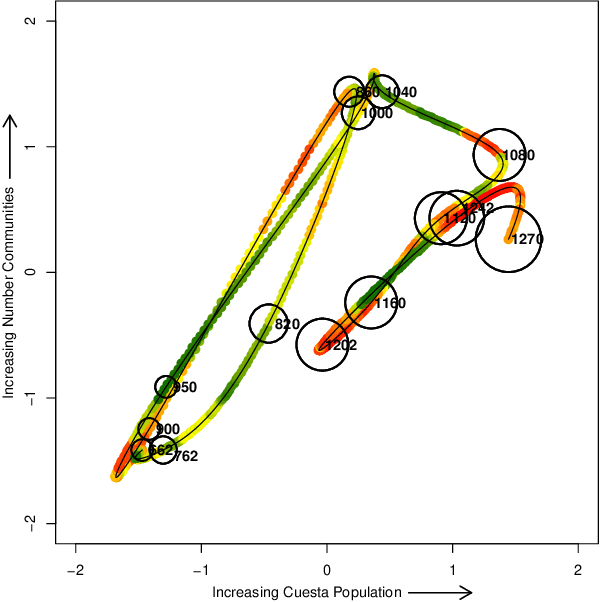
Historical processes manifest remarkable diversity. Nevertheless, scholars have long attempted to identify patterns and categorize historical actors and influences with some success. A stochastic process framework provides a structured approach for the analysis of large historical datasets that allows for detection of sometimes surprising patterns, identification of relevant causal actors both endogenous and exogenous to the process, and comparison between different historical cases. The combination of data, analytical tools and the organizing theoretical framework of stochastic processes complements traditional narrative approaches in history and archaeology.