Towards practical reinforcement learning for tokamak magnetic control

Reinforcement learning (RL) has shown promising results for real-time control systems, including the domain of plasma magnetic control. However, there are still significant drawbacks compared to traditional feedback control approaches for magnetic confinement. In this work, we address key drawbacks of the RL method; achieving higher control accuracy for desired plasma properties, reducing the steady-state error, and decreasing the required time to learn new tasks. We build on top of \cite{degrave2022magnetic}, and present algorithmic improvements to the agent architecture and training procedure. We present simulation results that show up to 65\% improvement in shape accuracy, achieve substantial reduction in the long-term bias of the plasma current, and additionally reduce the training time required to learn new tasks by a factor of 3 or more. We present new experiments using the upgraded RL-based controllers on the TCV tokamak, which validate the simulation results achieved, and point the way towards routinely achieving accurate discharges using the RL approach.

From Motor Control to Team Play in Simulated Humanoid Football

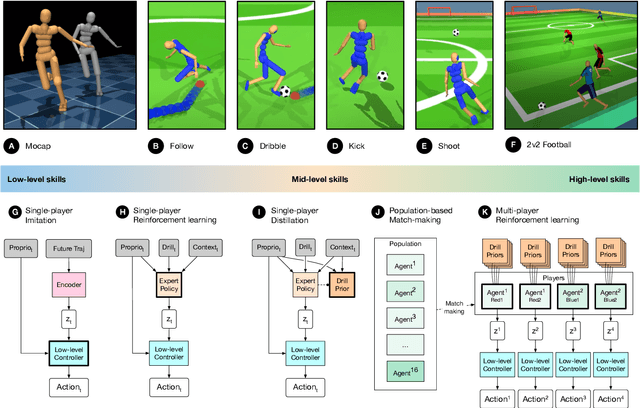
Intelligent behaviour in the physical world exhibits structure at multiple spatial and temporal scales. Although movements are ultimately executed at the level of instantaneous muscle tensions or joint torques, they must be selected to serve goals defined on much longer timescales, and in terms of relations that extend far beyond the body itself, ultimately involving coordination with other agents. Recent research in artificial intelligence has shown the promise of learning-based approaches to the respective problems of complex movement, longer-term planning and multi-agent coordination. However, there is limited research aimed at their integration. We study this problem by training teams of physically simulated humanoid avatars to play football in a realistic virtual environment. We develop a method that combines imitation learning, single- and multi-agent reinforcement learning and population-based training, and makes use of transferable representations of behaviour for decision making at different levels of abstraction. In a sequence of stages, players first learn to control a fully articulated body to perform realistic, human-like movements such as running and turning; they then acquire mid-level football skills such as dribbling and shooting; finally, they develop awareness of others and play as a team, bridging the gap between low-level motor control at a timescale of milliseconds, and coordinated goal-directed behaviour as a team at the timescale of tens of seconds. We investigate the emergence of behaviours at different levels of abstraction, as well as the representations that underlie these behaviours using several analysis techniques, including statistics from real-world sports analytics. Our work constitutes a complete demonstration of integrated decision-making at multiple scales in a physically embodied multi-agent setting. See project video at https://youtu.be/KHMwq9pv7mg.

Nonlinear Information Bottleneck

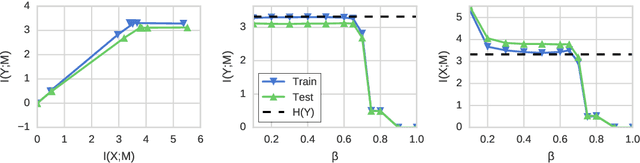
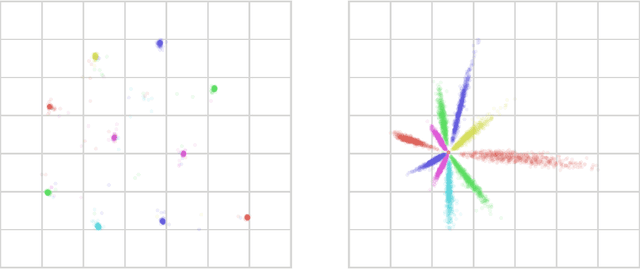
Information bottleneck [IB] is a technique for extracting information in some `input' random variable that is relevant for predicting some different 'output' random variable. IB works by encoding the input in a compressed 'bottleneck variable' from which the output can then be accurately decoded. IB can be difficult to compute in practice, and has been mainly developed for two limited cases: (1) discrete random variables with small state spaces, and (2) continuous random variables that are jointly Gaussian distributed (in which case the encoding and decoding maps are linear). We propose a method to perform IB in more general domains. Our approach can be applied to discrete or continuous inputs and outputs, and allows for nonlinear encoding and decoding maps. The method uses a novel upper bound on the IB objective, derived using a non-parametric estimator of mutual information and a variational approximation. We show how to implement the method using neural networks and gradient-based optimization, and demonstrate its performance on the MNIST dataset.

Pathologies in information bottleneck for deterministic supervised learning

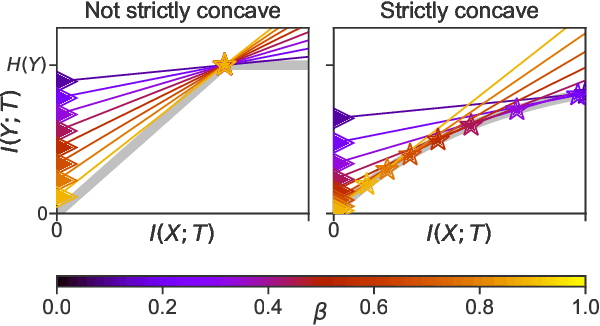
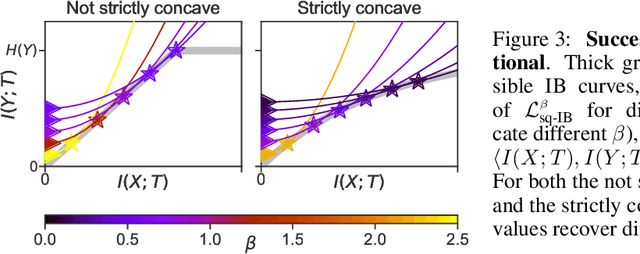
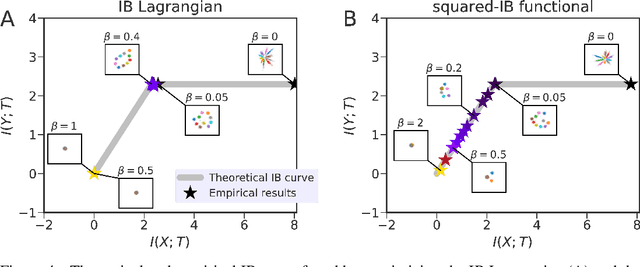
Information bottleneck (IB) is a method for extracting information from one random variable $X$ that is relevant for predicting another random variable $Y$. To do so, IB identifies an intermediate "bottleneck" variable $T$ that has low mutual information $I(X;T)$ and high mutual information $I(Y;T)$. The "IB curve" characterizes the set of bottleneck variables that achieve maximal $I(Y;T)$ for a given $I(X;T)$, and is typically explored by optimizing the "IB Lagrangian", $I(Y;T) - \beta I(X;T)$. Recently, there has been interest in applying IB to supervised learning, particularly for classification problems that use neural networks. In most classification problems, the output class $Y$ is a deterministic function of the input $X$, which we refer to as "deterministic supervised learning". We demonstrate three pathologies that arise when IB is used in any scenario where $Y$ is a deterministic function of $X$: (1) the IB curve cannot be recovered by optimizing the IB Lagrangian for different values of $\beta$; (2) there are "uninteresting" solutions at all points of the IB curve; and (3) for classifiers that achieve low error rates, the activity of different hidden layers will not exhibit a strict trade-off between compression and prediction, contrary to a recent proposal. To address problem (1), we propose a functional that, unlike the IB Lagrangian, can recover the IB curve in all cases. We finish by demonstrating these issues on the MNIST dataset.

Estimating Mixture Entropy with Pairwise Distances

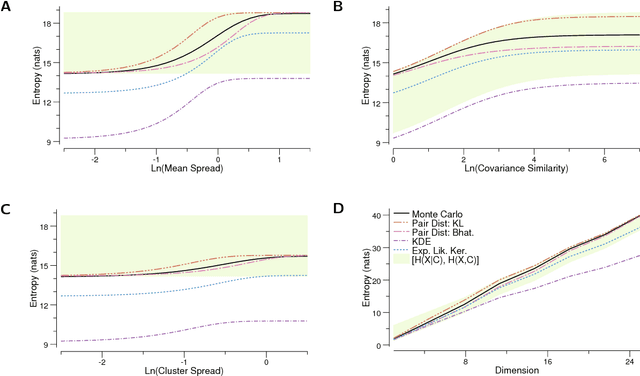
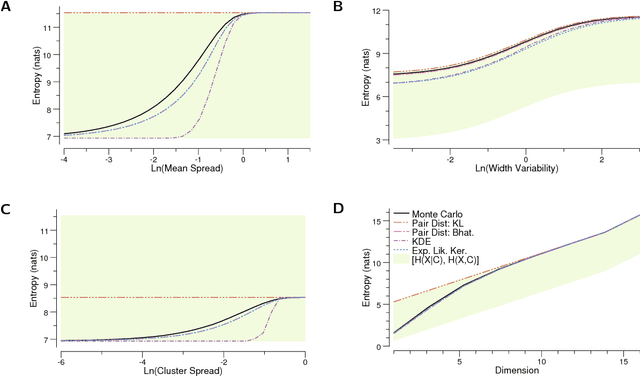
Mixture distributions arise in many parametric and non-parametric settings -- for example, in Gaussian mixture models and in non-parametric estimation. It is often necessary to compute the entropy of a mixture, but, in most cases, this quantity has no closed-form expression, making some form of approximation necessary. We propose a family of estimators based on a pairwise distance function between mixture components, and show that this estimator class has many attractive properties. For many distributions of interest, the proposed estimators are efficient to compute, differentiable in the mixture parameters, and become exact when the mixture components are clustered. We prove this family includes lower and upper bounds on the mixture entropy. The Chernoff $\alpha$-divergence gives a lower bound when chosen as the distance function, with the Bhattacharyya distance providing the tightest lower bound for components that are symmetric and members of a location family. The Kullback-Leibler divergence gives an upper bound when used as the distance function. We provide closed-form expressions of these bounds for mixtures of Gaussians, and discuss their applications to the estimation of mutual information. We then demonstrate that our bounds are significantly tighter than well-known existing bounds using numeric simulations. This estimator class is very useful in optimization problems involving maximization/minimization of entropy and mutual information, such as MaxEnt and rate distortion problems.

Upgrading from Gaussian Processes to Student's-T Processes

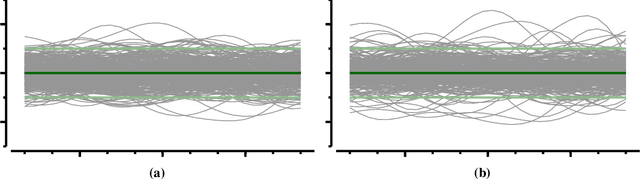
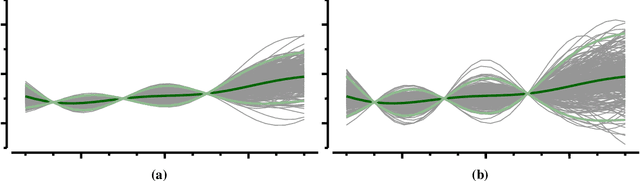
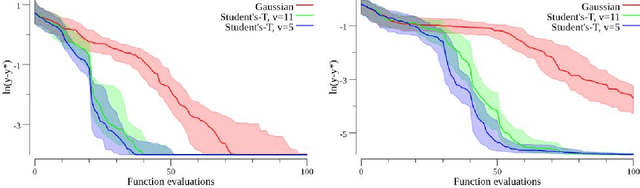
Gaussian process priors are commonly used in aerospace design for performing Bayesian optimization. Nonetheless, Gaussian processes suffer two significant drawbacks: outliers are a priori assumed unlikely, and the posterior variance conditioned on observed data depends only on the locations of those data, not the associated sample values. Student's-T processes are a generalization of Gaussian processes, founded on the Student's-T distribution instead of the Gaussian distribution. Student's-T processes maintain the primary advantages of Gaussian processes (kernel function, analytic update rule) with additional benefits beyond Gaussian processes. The Student's-T distribution has higher Kurtosis than a Gaussian distribution and so outliers are much more likely, and the posterior variance increases or decreases depending on the variance of observed data sample values. Here, we describe Student's-T processes, and discuss their advantages in the context of aerospace optimization. We show how to construct a Student's-T process using a kernel function and how to update the process given new samples. We provide a clear derivation of optimization-relevant quantities such as expected improvement, and contrast with the related computations for Gaussian processes. Finally, we compare the performance of Student's-T processes against Gaussian process on canonical test problems in Bayesian optimization, and apply the Student's-T process to the optimization of an aerostructural design problem.

Deep Reinforcement Learning for Event-Driven Multi-Agent Decision Processes

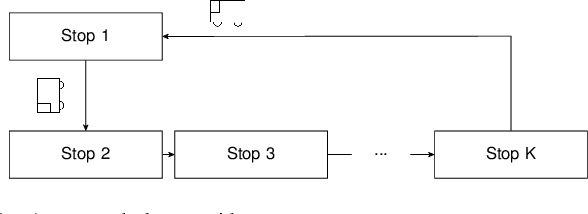
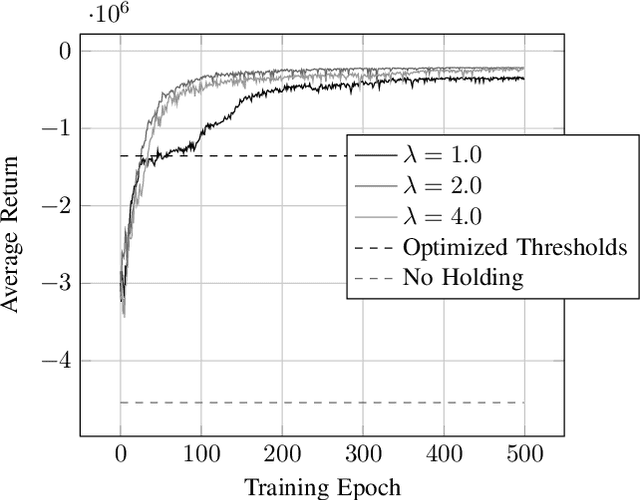
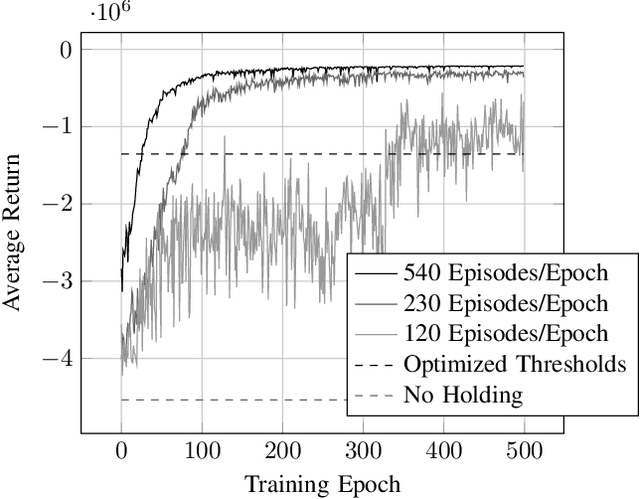
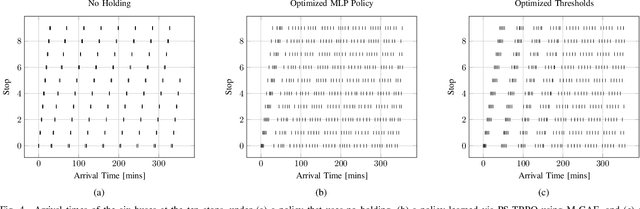
The incorporation of macro-actions (temporally extended actions) into multi-agent decision problems has the potential to address the curse of dimensionality associated with such decision problems. Since macro-actions last for stochastic durations, multiple agents executing decentralized policies in cooperative environments must act asynchronously. We present an algorithm that modifies Generalized Advantage Estimation for temporally extended actions, allowing a state-of-the-art policy optimization algorithm to optimize policies in Dec-POMDPs in which agents act asynchronously. We show that our algorithm is capable of learning optimal policies in two cooperative domains, one involving real-time bus holding control and one involving wildfire fighting with unmanned aircraft. Our algorithm works by framing problems as "event-driven decision processes," which are scenarios where the sequence and timing of actions and events are random and governed by an underlying stochastic process. In addition to optimizing policies with continuous state and action spaces, our algorithm also facilitates the use of event-driven simulators, which do not require time to be discretized into time-steps. We demonstrate the benefit of using event-driven simulation in the context of multiple agents taking asynchronous actions. We show that fixed time-step simulation risks obfuscating the sequence in which closely-separated events occur, adversely affecting the policies learned. Additionally, we show that arbitrarily shrinking the time-step scales poorly with the number of agents.

Reducing the error of Monte Carlo Algorithms by Learning Control Variates

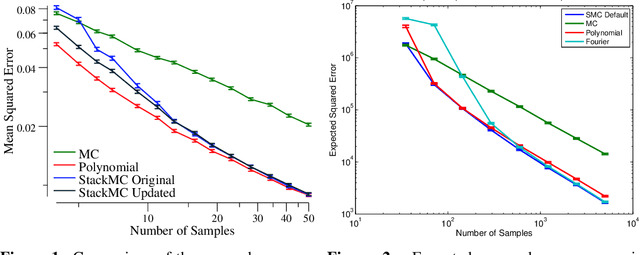
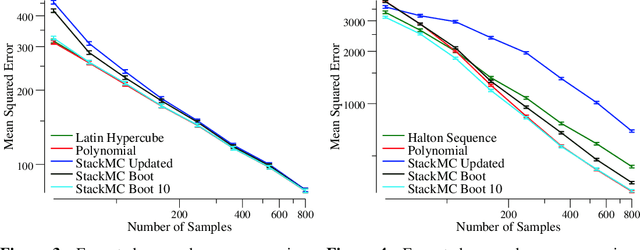
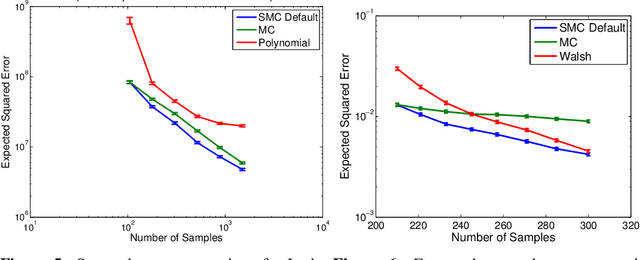
Monte Carlo (MC) sampling algorithms are an extremely widely-used technique to estimate expectations of functions f(x), especially in high dimensions. Control variates are a very powerful technique to reduce the error of such estimates, but in their conventional form rely on having an accurate approximation of f, a priori. Stacked Monte Carlo (StackMC) is a recently introduced technique designed to overcome this limitation by fitting a control variate to the data samples themselves. Done naively, forming a control variate to the data would result in overfitting, typically worsening the MC algorithm's performance. StackMC uses in-sample / out-sample techniques to remove this overfitting. Crucially, it is a post-processing technique, requiring no additional samples, and can be applied to data generated by any MC estimator. Our preliminary experiments demonstrated that StackMC improved the estimates of expectations when it was used to post-process samples produces by a "simple sampling" MC estimator. Here we substantially extend this earlier work. We provide an in-depth analysis of the StackMC algorithm, which we use to construct an improved version of the original algorithm, with lower estimation error. We then perform experiments of StackMC on several additional kinds of MC estimators, demonstrating improved performance when the samples are generated via importance sampling, Latin-hypercube sampling and quasi-Monte Carlo sampling. We also show how to extend StackMC to combine multiple fitting functions, and how to apply it to discrete input spaces x.