Deep Reinforcement Learning for Event-Driven Multi-Agent Decision Processes

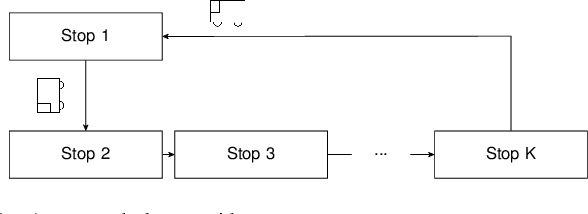
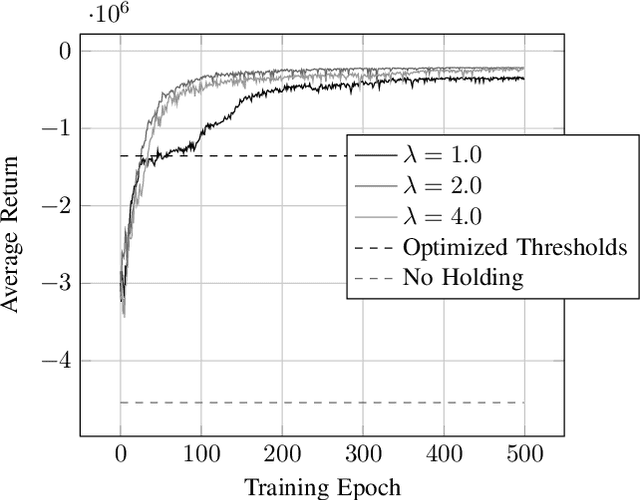
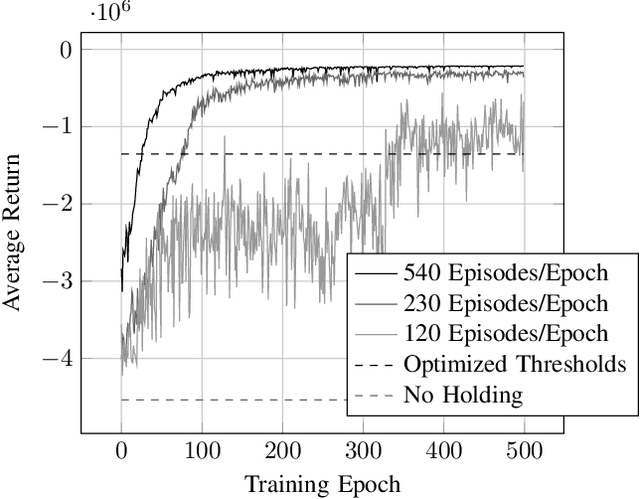
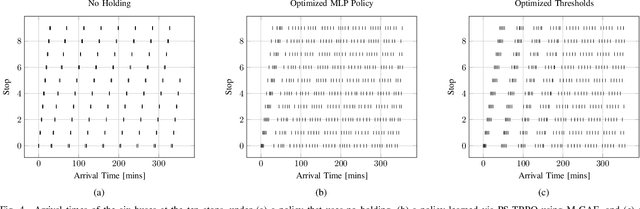
The incorporation of macro-actions (temporally extended actions) into multi-agent decision problems has the potential to address the curse of dimensionality associated with such decision problems. Since macro-actions last for stochastic durations, multiple agents executing decentralized policies in cooperative environments must act asynchronously. We present an algorithm that modifies Generalized Advantage Estimation for temporally extended actions, allowing a state-of-the-art policy optimization algorithm to optimize policies in Dec-POMDPs in which agents act asynchronously. We show that our algorithm is capable of learning optimal policies in two cooperative domains, one involving real-time bus holding control and one involving wildfire fighting with unmanned aircraft. Our algorithm works by framing problems as "event-driven decision processes," which are scenarios where the sequence and timing of actions and events are random and governed by an underlying stochastic process. In addition to optimizing policies with continuous state and action spaces, our algorithm also facilitates the use of event-driven simulators, which do not require time to be discretized into time-steps. We demonstrate the benefit of using event-driven simulation in the context of multiple agents taking asynchronous actions. We show that fixed time-step simulation risks obfuscating the sequence in which closely-separated events occur, adversely affecting the policies learned. Additionally, we show that arbitrarily shrinking the time-step scales poorly with the number of agents.

Using Supervised Learning to Improve Monte Carlo Integral Estimation

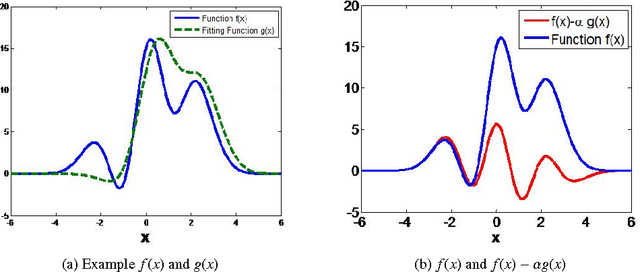
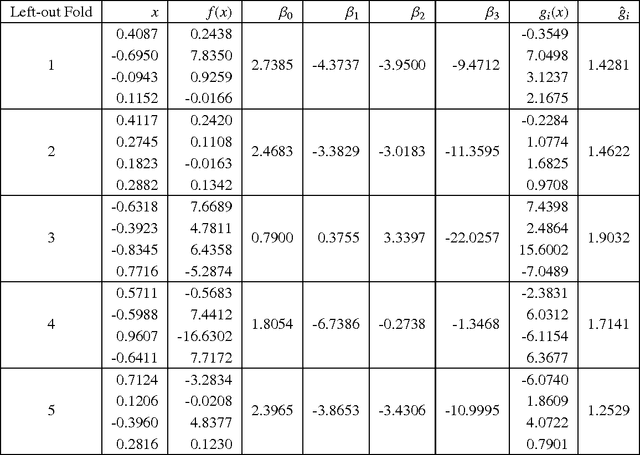
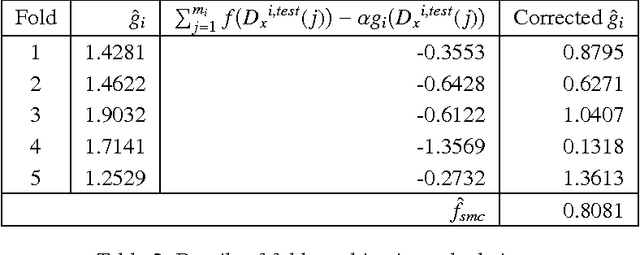
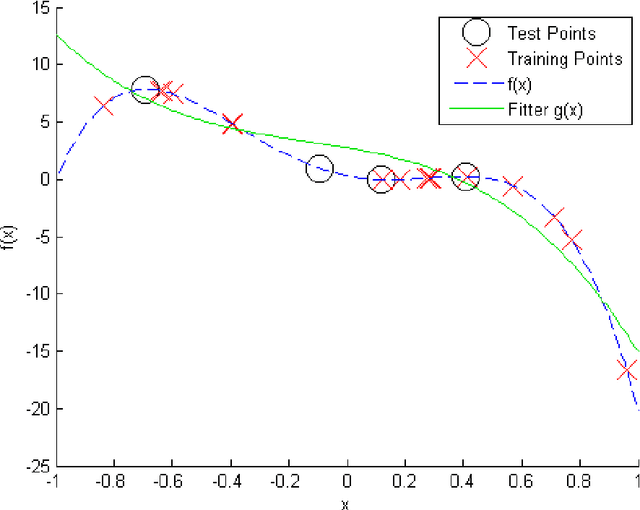
Monte Carlo (MC) techniques are often used to estimate integrals of a multivariate function using randomly generated samples of the function. In light of the increasing interest in uncertainty quantification and robust design applications in aerospace engineering, the calculation of expected values of such functions (e.g. performance measures) becomes important. However, MC techniques often suffer from high variance and slow convergence as the number of samples increases. In this paper we present Stacked Monte Carlo (StackMC), a new method for post-processing an existing set of MC samples to improve the associated integral estimate. StackMC is based on the supervised learning techniques of fitting functions and cross validation. It should reduce the variance of any type of Monte Carlo integral estimate (simple sampling, importance sampling, quasi-Monte Carlo, MCMC, etc.) without adding bias. We report on an extensive set of experiments confirming that the StackMC estimate of an integral is more accurate than both the associated unprocessed Monte Carlo estimate and an estimate based on a functional fit to the MC samples. These experiments run over a wide variety of integration spaces, numbers of sample points, dimensions, and fitting functions. In particular, we apply StackMC in estimating the expected value of the fuel burn metric of future commercial aircraft and in estimating sonic boom loudness measures. We compare the efficiency of StackMC with that of more standard methods and show that for negligible additional computational cost significant increases in accuracy are gained.

Distributed Constrained Optimization with Semicoordinate Transformations

Recent work has shown how information theory extends conventional full-rationality game theory to allow bounded rational agents. The associated mathematical framework can be used to solve constrained optimization problems. This is done by translating the problem into an iterated game, where each agent controls a different variable of the problem, so that the joint probability distribution across the agents' moves gives an expected value of the objective function. The dynamics of the agents is designed to minimize a Lagrangian function of that joint distribution. Here we illustrate how the updating of the Lagrange parameters in the Lagrangian is a form of automated annealing, which focuses the joint distribution more and more tightly about the joint moves that optimize the objective function. We then investigate the use of ``semicoordinate'' variable transformations. These separate the joint state of the agents from the variables of the optimization problem, with the two connected by an onto mapping. We present experiments illustrating the ability of such transformations to facilitate optimization. We focus on the special kind of transformation in which the statistically independent states of the agents induces a mixture distribution over the optimization variables. Computer experiment illustrate this for $k$-sat constraint satisfaction problems and for unconstrained minimization of $NK$ functions.

Bias-Variance Techniques for Monte Carlo Optimization: Cross-validation for the CE Method

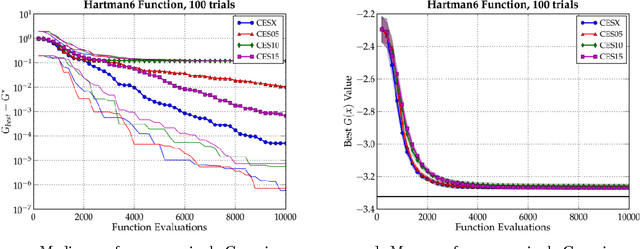
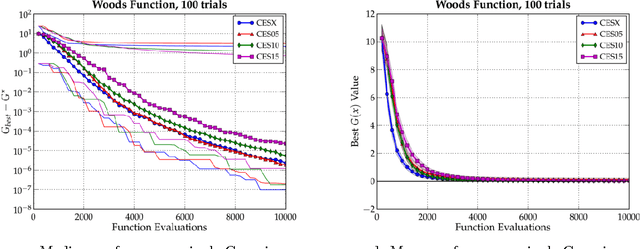
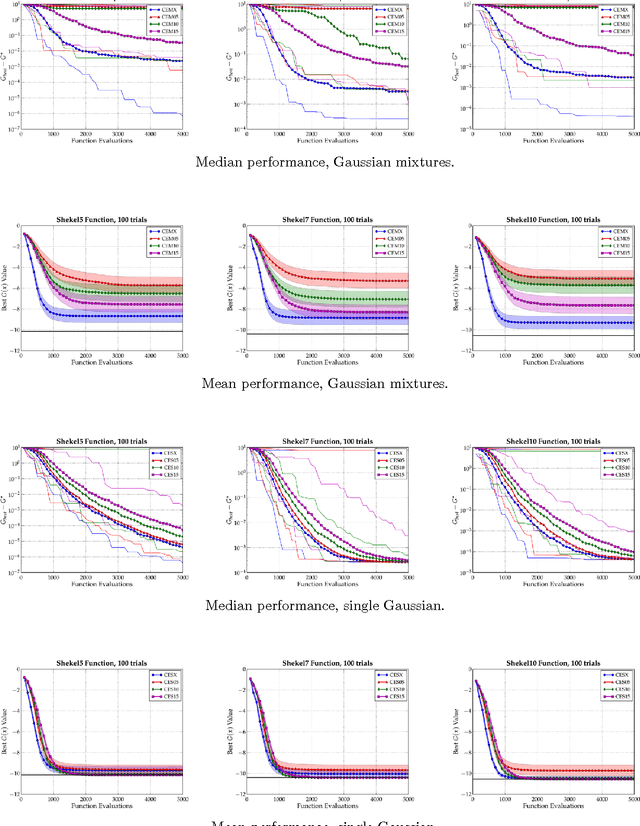
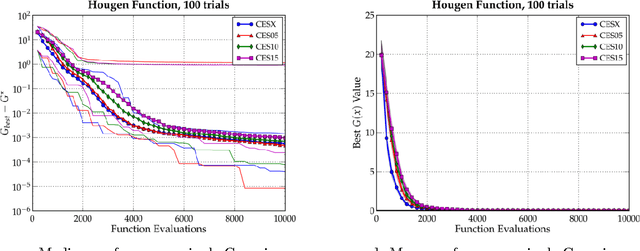
In this paper, we examine the CE method in the broad context of Monte Carlo Optimization (MCO) and Parametric Learning (PL), a type of machine learning. A well-known overarching principle used to improve the performance of many PL algorithms is the bias-variance tradeoff. This tradeoff has been used to improve PL algorithms ranging from Monte Carlo estimation of integrals, to linear estimation, to general statistical estimation. Moreover, as described by, MCO is very closely related to PL. Owing to this similarity, the bias-variance tradeoff affects MCO performance, just as it does PL performance. In this article, we exploit the bias-variance tradeoff to enhance the performance of MCO algorithms. We use the technique of cross-validation, a technique based on the bias-variance tradeoff, to significantly improve the performance of the Cross Entropy (CE) method, which is an MCO algorithm. In previous work we have confirmed that other PL techniques improve the perfomance of other MCO algorithms. We conclude that the many techniques pioneered in PL could be investigated as ways to improve MCO algorithms in general, and the CE method in particular.