A Multi-fidelity Double-Delta Wing Dataset and Empirical Scaling Laws for GNN-based Aerodynamic Field Surrogate

Data-driven surrogate models are increasingly adopted to accelerate vehicle design. However, open-source multi-fidelity datasets and empirical guidelines linking dataset size to model performance remain limited. This study investigates the relationship between training data size and prediction accuracy for a graph neural network (GNN) based surrogate model for aerodynamic field prediction. We release an open-source, multi-fidelity aerodynamic dataset for double-delta wings, comprising 2448 flow snapshots across 272 geometries evaluated at angles of attack from 11 (degree) to 19 (degree) at Ma=0.3 using both Vortex Lattice Method (VLM) and Reynolds-Averaged Navier-Stokes (RANS) solvers. The geometries are generated using a nested Saltelli sampling scheme to support future dataset expansion and variance-based sensitivity analysis. Using this dataset, we conduct a preliminary empirical scaling study of the MF-VortexNet surrogate by constructing six training datasets with sizes ranging from 40 to 1280 snapshots and training models with 0.1 to 2.4 million parameters under a fixed training budget. We find that the test error decreases with data size with a power-law exponent of -0.6122, indicating efficient data utilization. Based on this scaling law, we estimate that the optimal sampling density is approximately eight samples per dimension in a d-dimensional design space. The results also suggest improved data utilization efficiency for larger surrogate models, implying a potential trade-off between dataset generation cost and model training budget.

Using Supervised Learning to Improve Monte Carlo Integral Estimation

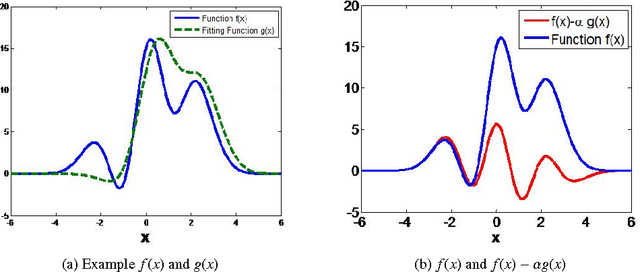
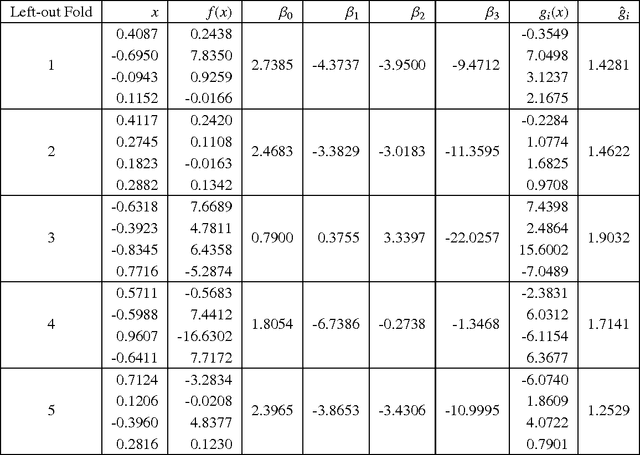
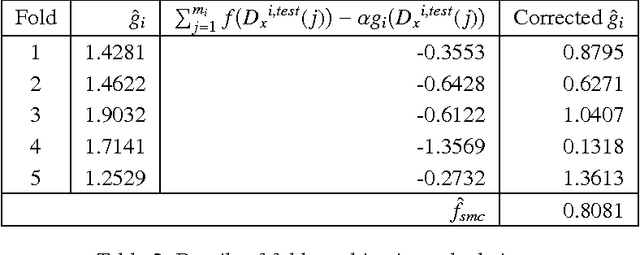
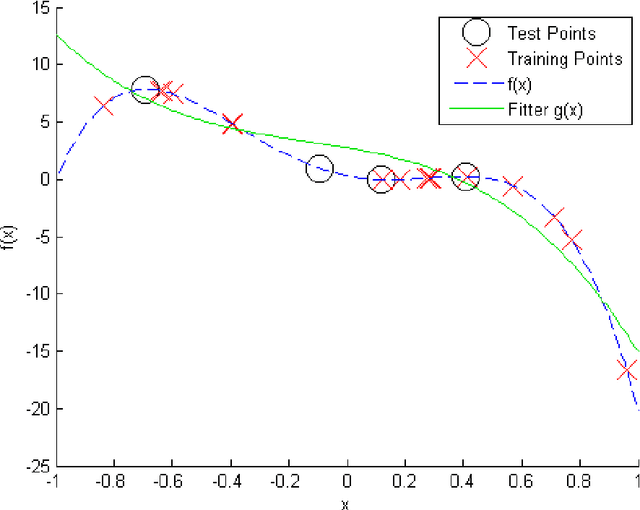
Monte Carlo (MC) techniques are often used to estimate integrals of a multivariate function using randomly generated samples of the function. In light of the increasing interest in uncertainty quantification and robust design applications in aerospace engineering, the calculation of expected values of such functions (e.g. performance measures) becomes important. However, MC techniques often suffer from high variance and slow convergence as the number of samples increases. In this paper we present Stacked Monte Carlo (StackMC), a new method for post-processing an existing set of MC samples to improve the associated integral estimate. StackMC is based on the supervised learning techniques of fitting functions and cross validation. It should reduce the variance of any type of Monte Carlo integral estimate (simple sampling, importance sampling, quasi-Monte Carlo, MCMC, etc.) without adding bias. We report on an extensive set of experiments confirming that the StackMC estimate of an integral is more accurate than both the associated unprocessed Monte Carlo estimate and an estimate based on a functional fit to the MC samples. These experiments run over a wide variety of integration spaces, numbers of sample points, dimensions, and fitting functions. In particular, we apply StackMC in estimating the expected value of the fuel burn metric of future commercial aircraft and in estimating sonic boom loudness measures. We compare the efficiency of StackMC with that of more standard methods and show that for negligible additional computational cost significant increases in accuracy are gained.