Improving cosmological reach of a gravitational wave observatory using Deep Loop Shaping

Improved low-frequency sensitivity of gravitational wave observatories would unlock study of intermediate-mass black hole mergers, binary black hole eccentricity, and provide early warnings for multi-messenger observations of binary neutron star mergers. Today's mirror stabilization control injects harmful noise, constituting a major obstacle to sensitivity improvements. We eliminated this noise through Deep Loop Shaping, a reinforcement learning method using frequency domain rewards. We proved our methodology on the LIGO Livingston Observatory (LLO). Our controller reduced control noise in the 10--30Hz band by over 30x, and up to 100x in sub-bands surpassing the design goal motivated by the quantum limit. These results highlight the potential of Deep Loop Shaping to improve current and future GW observatories, and more broadly instrumentation and control systems.

Wasserstein Policy Optimization

We introduce Wasserstein Policy Optimization (WPO), an actor-critic algorithm for reinforcement learning in continuous action spaces. WPO can be derived as an approximation to Wasserstein gradient flow over the space of all policies projected into a finite-dimensional parameter space (e.g., the weights of a neural network), leading to a simple and completely general closed-form update. The resulting algorithm combines many properties of deterministic and classic policy gradient methods. Like deterministic policy gradients, it exploits knowledge of the gradient of the action-value function with respect to the action. Like classic policy gradients, it can be applied to stochastic policies with arbitrary distributions over actions -- without using the reparameterization trick. We show results on the DeepMind Control Suite and a magnetic confinement fusion task which compare favorably with state-of-the-art continuous control methods.

Real World Games Look Like Spinning Tops

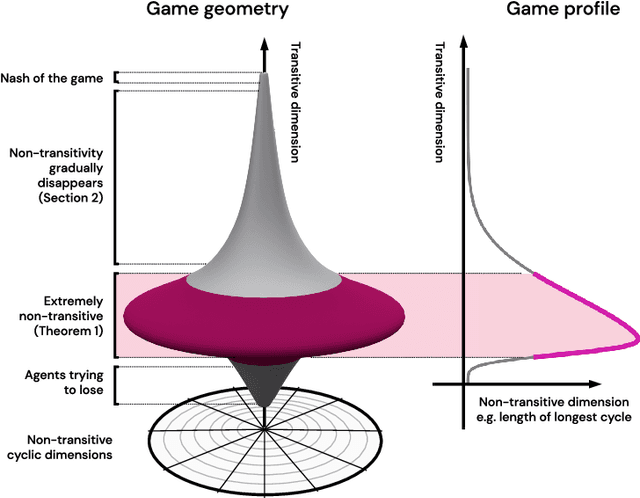
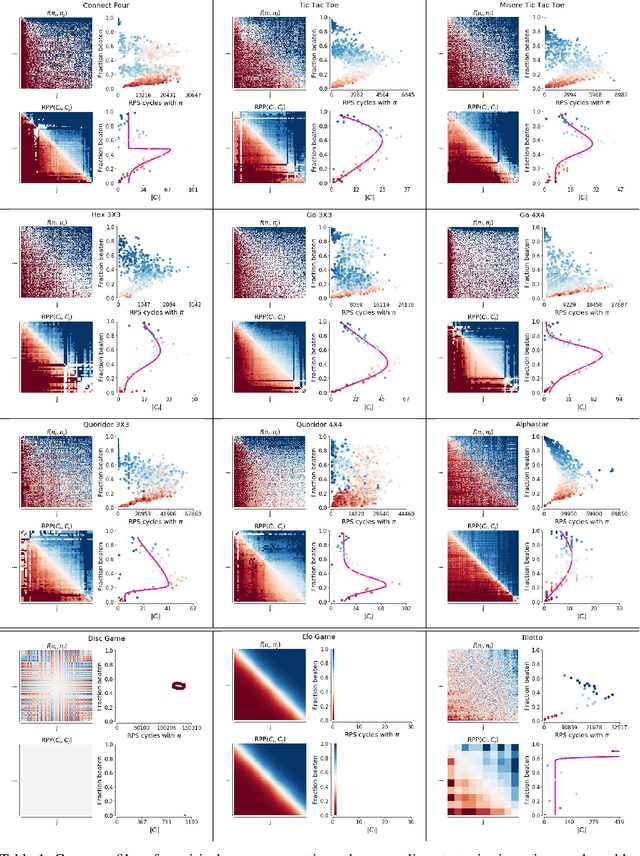
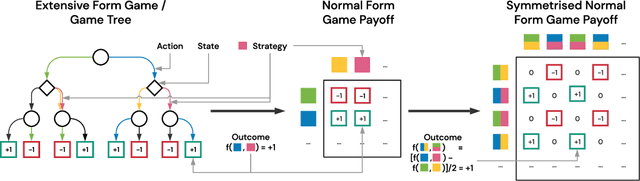
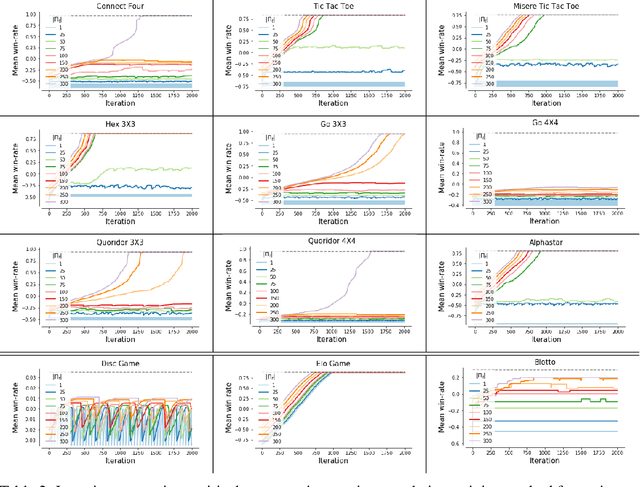
This paper investigates the geometrical properties of real world games (e.g. Tic-Tac-Toe, Go, StarCraft II). We hypothesise that their geometrical structure resemble a spinning top, with the upright axis representing transitive strength, and the radial axis, which corresponds to the number of cycles that exist at a particular transitive strength, representing the non-transitive dimension. We prove the existence of this geometry for a wide class of real world games, exposing their temporal nature. Additionally, we show that this unique structure also has consequences for learning - it clarifies why populations of strategies are necessary for training of agents, and how population size relates to the structure of the game. Finally, we empirically validate these claims by using a selection of nine real world two-player zero-sum symmetric games, showing 1) the spinning top structure is revealed and can be easily re-constructed by using a new method of Nash clustering to measure the interaction between transitive and cyclical strategy behaviour, and 2) the effect that population size has on the convergence in these games.

Predicting the behavior of interacting humans by fusing data from multiple sources

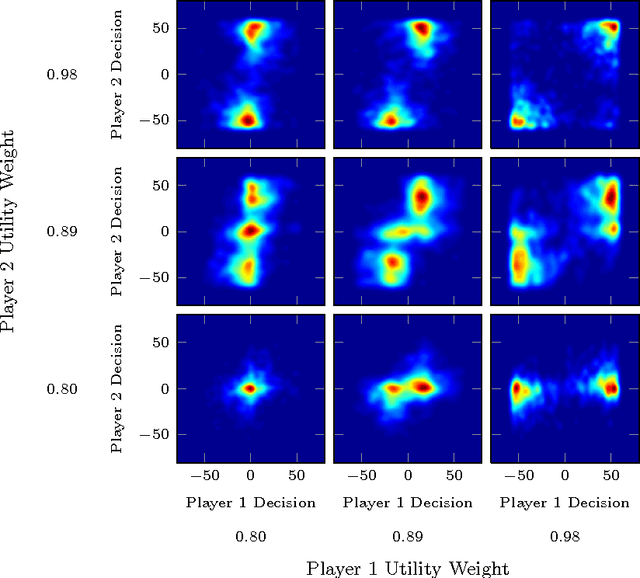
Multi-fidelity methods combine inexpensive low-fidelity simulations with costly but highfidelity simulations to produce an accurate model of a system of interest at minimal cost. They have proven useful in modeling physical systems and have been applied to engineering problems such as wing-design optimization. During human-in-the-loop experimentation, it has become increasingly common to use online platforms, like Mechanical Turk, to run low-fidelity experiments to gather human performance data in an efficient manner. One concern with these experiments is that the results obtained from the online environment generalize poorly to the actual domain of interest. To address this limitation, we extend traditional multi-fidelity approaches to allow us to combine fewer data points from high-fidelity human-in-the-loop experiments with plentiful but less accurate data from low-fidelity experiments to produce accurate models of how humans interact. We present both model-based and model-free methods, and summarize the predictive performance of each method under dierent conditions.

Using Supervised Learning to Improve Monte Carlo Integral Estimation

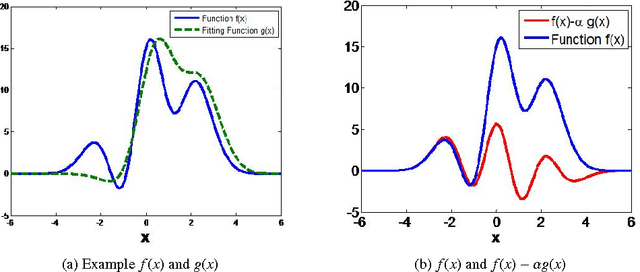
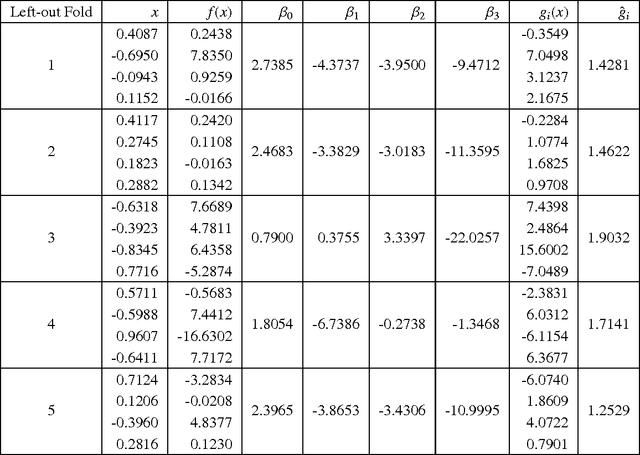
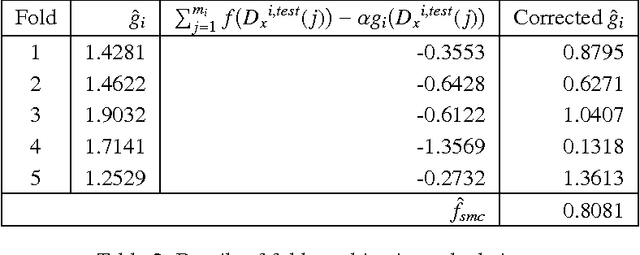
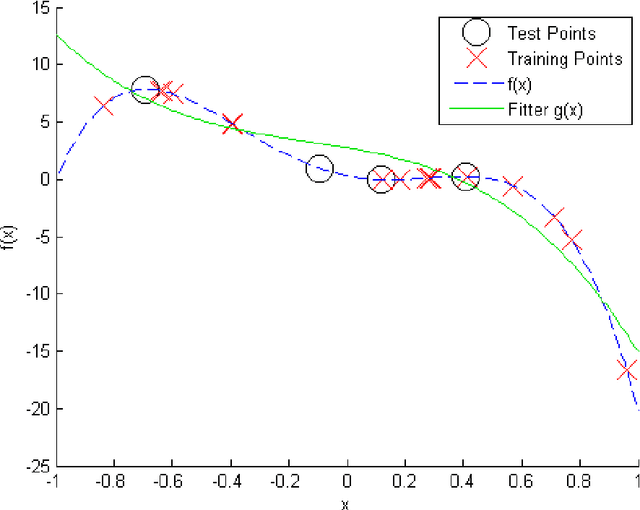
Monte Carlo (MC) techniques are often used to estimate integrals of a multivariate function using randomly generated samples of the function. In light of the increasing interest in uncertainty quantification and robust design applications in aerospace engineering, the calculation of expected values of such functions (e.g. performance measures) becomes important. However, MC techniques often suffer from high variance and slow convergence as the number of samples increases. In this paper we present Stacked Monte Carlo (StackMC), a new method for post-processing an existing set of MC samples to improve the associated integral estimate. StackMC is based on the supervised learning techniques of fitting functions and cross validation. It should reduce the variance of any type of Monte Carlo integral estimate (simple sampling, importance sampling, quasi-Monte Carlo, MCMC, etc.) without adding bias. We report on an extensive set of experiments confirming that the StackMC estimate of an integral is more accurate than both the associated unprocessed Monte Carlo estimate and an estimate based on a functional fit to the MC samples. These experiments run over a wide variety of integration spaces, numbers of sample points, dimensions, and fitting functions. In particular, we apply StackMC in estimating the expected value of the fuel burn metric of future commercial aircraft and in estimating sonic boom loudness measures. We compare the efficiency of StackMC with that of more standard methods and show that for negligible additional computational cost significant increases in accuracy are gained.