Real World Games Look Like Spinning Tops
Paper and Code
Apr 20, 2020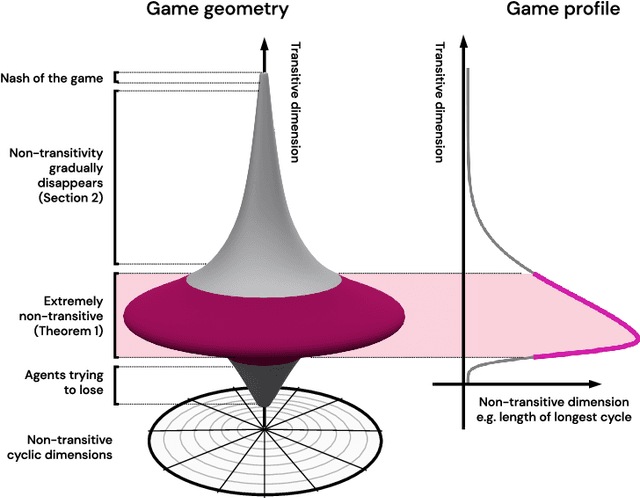
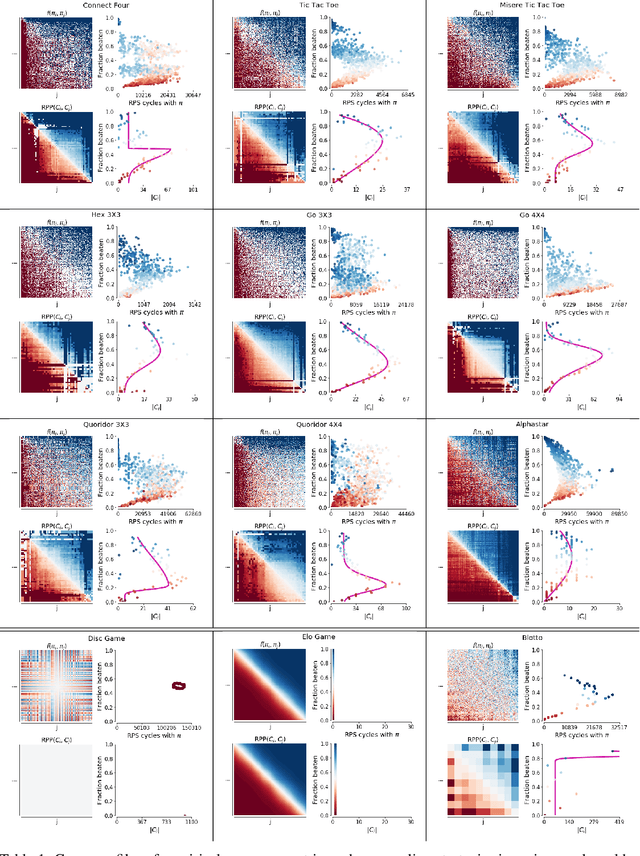
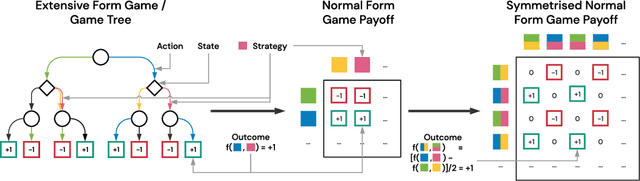
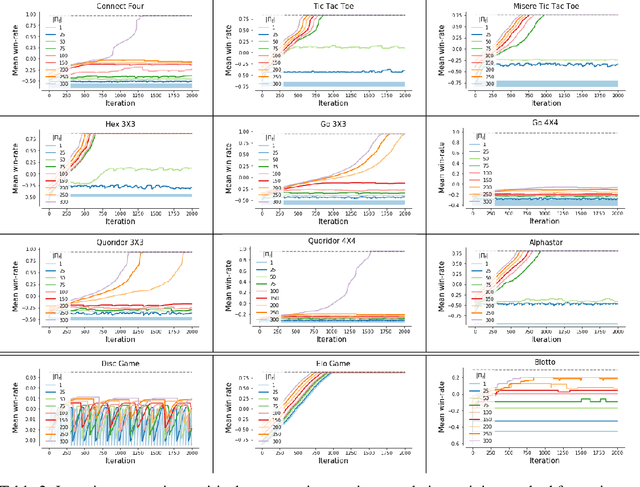
This paper investigates the geometrical properties of real world games (e.g. Tic-Tac-Toe, Go, StarCraft II). We hypothesise that their geometrical structure resemble a spinning top, with the upright axis representing transitive strength, and the radial axis, which corresponds to the number of cycles that exist at a particular transitive strength, representing the non-transitive dimension. We prove the existence of this geometry for a wide class of real world games, exposing their temporal nature. Additionally, we show that this unique structure also has consequences for learning - it clarifies why populations of strategies are necessary for training of agents, and how population size relates to the structure of the game. Finally, we empirically validate these claims by using a selection of nine real world two-player zero-sum symmetric games, showing 1) the spinning top structure is revealed and can be easily re-constructed by using a new method of Nash clustering to measure the interaction between transitive and cyclical strategy behaviour, and 2) the effect that population size has on the convergence in these games.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge