Pick Your Battles: Interaction Graphs as Population-Level Objectives for Strategic Diversity

Strategic diversity is often essential in games: in multi-player games, for example, evaluating a player against a diverse set of strategies will yield a more accurate estimate of its performance. Furthermore, in games with non-transitivities diversity allows a player to cover several winning strategies. However, despite the significance of strategic diversity, training agents that exhibit diverse behaviour remains a challenge. In this paper we study how to construct diverse populations of agents by carefully structuring how individuals within a population interact. Our approach is based on interaction graphs, which control the flow of information between agents during training and can encourage agents to specialise on different strategies, leading to improved overall performance. We provide evidence for the importance of diversity in multi-agent training and analyse the effect of applying different interaction graphs on the training trajectories, diversity and performance of populations in a range of games. This is an extended version of the long abstract published at AAMAS.

Real World Games Look Like Spinning Tops

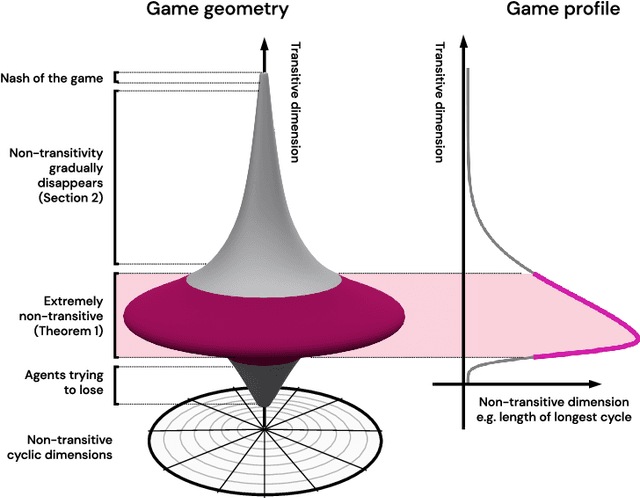
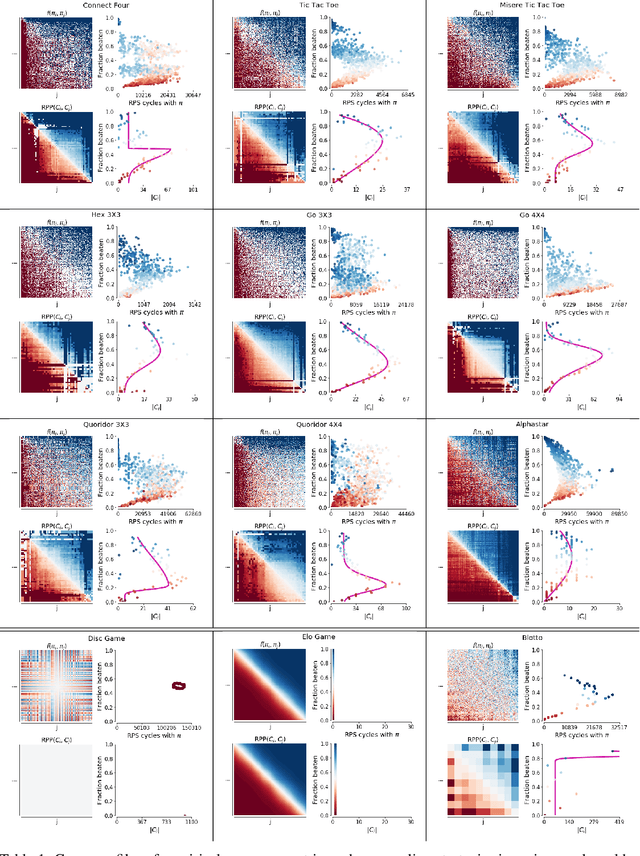
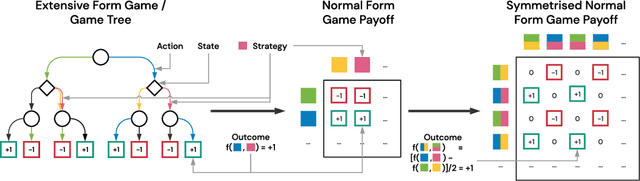
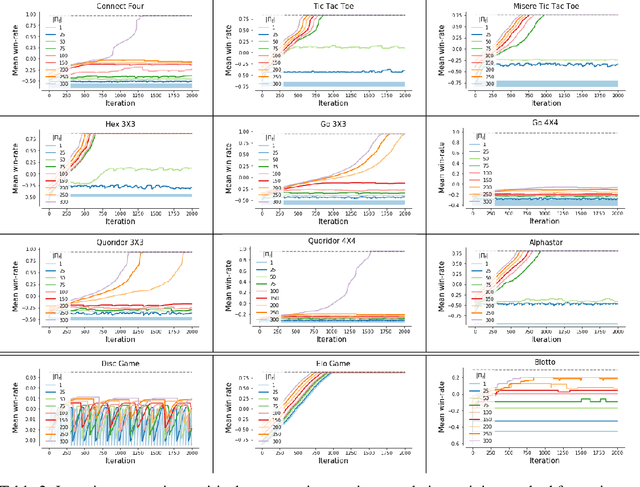
This paper investigates the geometrical properties of real world games (e.g. Tic-Tac-Toe, Go, StarCraft II). We hypothesise that their geometrical structure resemble a spinning top, with the upright axis representing transitive strength, and the radial axis, which corresponds to the number of cycles that exist at a particular transitive strength, representing the non-transitive dimension. We prove the existence of this geometry for a wide class of real world games, exposing their temporal nature. Additionally, we show that this unique structure also has consequences for learning - it clarifies why populations of strategies are necessary for training of agents, and how population size relates to the structure of the game. Finally, we empirically validate these claims by using a selection of nine real world two-player zero-sum symmetric games, showing 1) the spinning top structure is revealed and can be easily re-constructed by using a new method of Nash clustering to measure the interaction between transitive and cyclical strategy behaviour, and 2) the effect that population size has on the convergence in these games.

Learning to Resolve Alliance Dilemmas in Many-Player Zero-Sum Games

Zero-sum games have long guided artificial intelligence research, since they possess both a rich strategy space of best-responses and a clear evaluation metric. What's more, competition is a vital mechanism in many real-world multi-agent systems capable of generating intelligent innovations: Darwinian evolution, the market economy and the AlphaZero algorithm, to name a few. In two-player zero-sum games, the challenge is usually viewed as finding Nash equilibrium strategies, safeguarding against exploitation regardless of the opponent. While this captures the intricacies of chess or Go, it avoids the notion of cooperation with co-players, a hallmark of the major transitions leading from unicellular organisms to human civilization. Beyond two players, alliance formation often confers an advantage; however this requires trust, namely the promise of mutual cooperation in the face of incentives to defect. Successful play therefore requires adaptation to co-players rather than the pursuit of non-exploitability. Here we argue that a systematic study of many-player zero-sum games is a crucial element of artificial intelligence research. Using symmetric zero-sum matrix games, we demonstrate formally that alliance formation may be seen as a social dilemma, and empirically that na\"ive multi-agent reinforcement learning therefore fails to form alliances. We introduce a toy model of economic competition, and show how reinforcement learning may be augmented with a peer-to-peer contract mechanism to discover and enforce alliances. Finally, we generalize our agent model to incorporate temporally-extended contracts, presenting opportunities for further work.

From Poincaré Recurrence to Convergence in Imperfect Information Games: Finding Equilibrium via Regularization

In this paper we investigate the Follow the Regularized Leader dynamics in sequential imperfect information games (IIG). We generalize existing results of Poincar\'e recurrence from normal-form games to zero-sum two-player imperfect information games and other sequential game settings. We then investigate how adapting the reward (by adding a regularization term) of the game can give strong convergence guarantees in monotone games. We continue by showing how this reward adaptation technique can be leveraged to build algorithms that converge exactly to the Nash equilibrium. Finally, we show how these insights can be directly used to build state-of-the-art model-free algorithms for zero-sum two-player Imperfect Information Games (IIG).

Minimax Theorem for Latent Games or: How I Learned to Stop Worrying about Mixed-Nash and Love Neural Nets

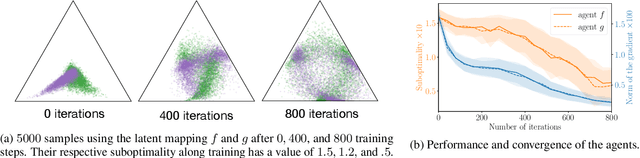
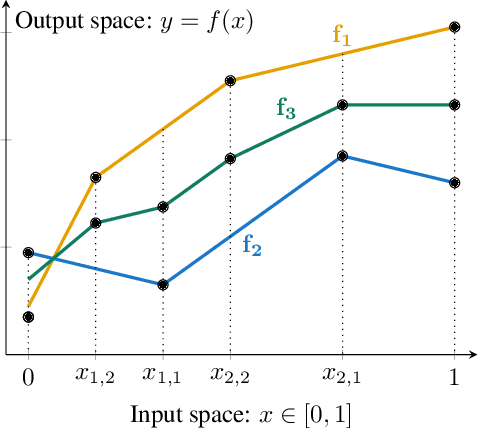
Adversarial training, a special case of multi-objective optimization, is an increasingly useful tool in machine learning. For example, two-player zero-sum games are important for generative modeling (GANs) and for mastering games like Go or Poker via self-play. A classic result in Game Theory states that one must mix strategies, as pure equilibria may not exist. Surprisingly, machine learning practitioners typically train a \emph{single} pair of agents -- instead of a pair of mixtures -- going against Nash's principle. Our main contribution is a notion of limited-capacity-equilibrium for which, as capacity grows, optimal agents -- not mixtures -- can learn increasingly expressive and realistic behaviors. We define \emph{latent games}, a new class of game where agents are mappings that transform latent distributions. Examples include generators in GANs, which transform Gaussian noise into distributions on images, and StarCraft II agents, which transform sampled build orders into policies. We show that minimax equilibria in latent games can be approximated by a \emph{single} pair of dense neural networks. Finally, we apply our latent game approach to solve differentiable Blotto, a game with an infinite strategy space.

Smooth markets: A basic mechanism for organizing gradient-based learners

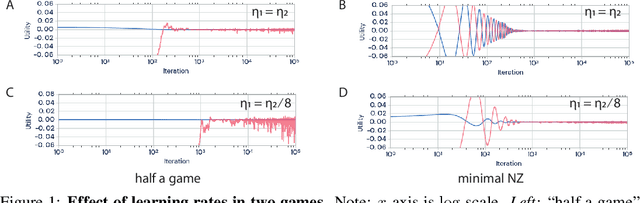
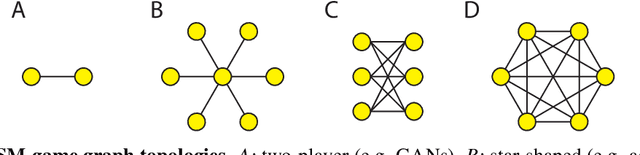
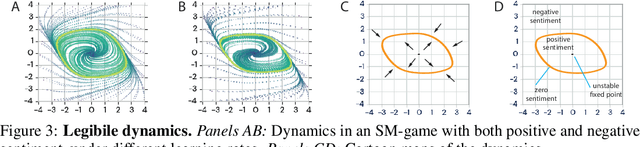
With the success of modern machine learning, it is becoming increasingly important to understand and control how learning algorithms interact. Unfortunately, negative results from game theory show there is little hope of understanding or controlling general n-player games. We therefore introduce smooth markets (SM-games), a class of n-player games with pairwise zero sum interactions. SM-games codify a common design pattern in machine learning that includes (some) GANs, adversarial training, and other recent algorithms. We show that SM-games are amenable to analysis and optimization using first-order methods.

LOGAN: Latent Optimisation for Generative Adversarial Networks

Training generative adversarial networks requires balancing of delicate adversarial dynamics. Even with careful tuning, training may diverge or end up in a bad equilibrium with dropped modes. In this work, we introduce a new form of latent optimisation inspired by the CS-GAN and show that it improves adversarial dynamics by enhancing interactions between the discriminator and the generator. We develop supporting theoretical analysis from the perspectives of differentiable games and stochastic approximation. Our experiments demonstrate that latent optimisation can significantly improve GAN training, obtaining state-of-the-art performance for the ImageNet (128 x 128) dataset. Our model achieves an Inception Score (IS) of 148 and an Fr\'echet Inception Distance (FID) of 3.4, an improvement of 17% and 32% in IS and FID respectively, compared with the baseline BigGAN-deep model with the same architecture and number of parameters.

Differentiable Game Mechanics

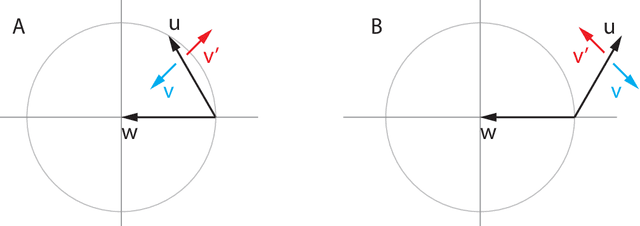
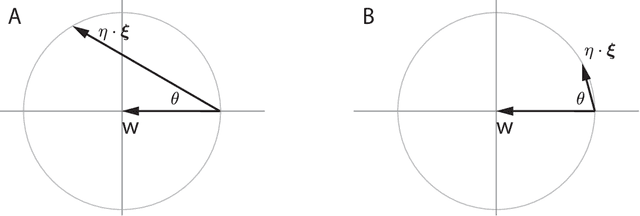
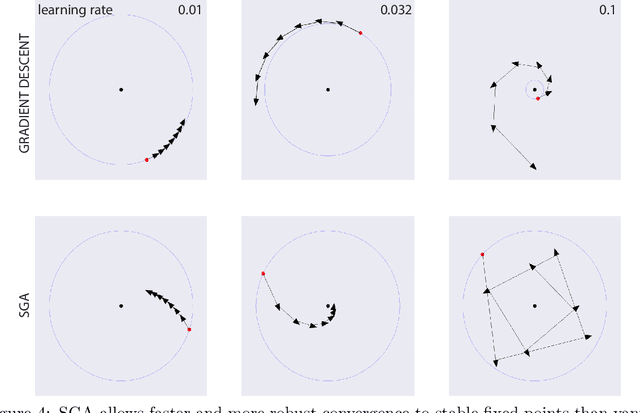
Deep learning is built on the foundational guarantee that gradient descent on an objective function converges to local minima. Unfortunately, this guarantee fails in settings, such as generative adversarial nets, that exhibit multiple interacting losses. The behavior of gradient-based methods in games is not well understood -- and is becoming increasingly important as adversarial and multi-objective architectures proliferate. In this paper, we develop new tools to understand and control the dynamics in n-player differentiable games. The key result is to decompose the game Jacobian into two components. The first, symmetric component, is related to potential games, which reduce to gradient descent on an implicit function. The second, antisymmetric component, relates to Hamiltonian games, a new class of games that obey a conservation law akin to conservation laws in classical mechanical systems. The decomposition motivates Symplectic Gradient Adjustment (SGA), a new algorithm for finding stable fixed points in differentiable games. Basic experiments show SGA is competitive with recently proposed algorithms for finding stable fixed points in GANs -- while at the same time being applicable to, and having guarantees in, much more general cases.

Open-ended Learning in Symmetric Zero-sum Games

Zero-sum games such as chess and poker are, abstractly, functions that evaluate pairs of agents, for example labeling them `winner' and `loser'. If the game is approximately transitive, then self-play generates sequences of agents of increasing strength. However, nontransitive games, such as rock-paper-scissors, can exhibit strategic cycles, and there is no longer a clear objective -- we want agents to increase in strength, but against whom is unclear. In this paper, we introduce a geometric framework for formulating agent objectives in zero-sum games, in order to construct adaptive sequences of objectives that yield open-ended learning. The framework allows us to reason about population performance in nontransitive games, and enables the development of a new algorithm (rectified Nash response, PSRO_rN) that uses game-theoretic niching to construct diverse populations of effective agents, producing a stronger set of agents than existing algorithms. We apply PSRO_rN to two highly nontransitive resource allocation games and find that PSRO_rN consistently outperforms the existing alternatives.

Stable Opponent Shaping in Differentiable Games

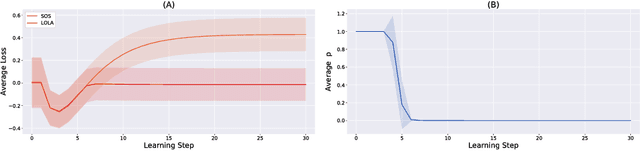
A growing number of learning methods are actually \emph{games} which optimise multiple, interdependent objectives in parallel -- from GANs and intrinsic curiosity to multi-agent RL. Opponent shaping is a powerful approach to improve learning dynamics in such games, accounting for the fact that the 'environment' includes agents adapting to one another's updates. Learning with Opponent-Learning Awareness (LOLA) is a recent algorithm which exploits this dynamic response and encourages cooperation in settings like the Iterated Prisoner's Dilemma. Although experimentally successful, we show that LOLA can exhibit 'arrogant' behaviour directly at odds with convergence. In fact, remarkably few algorithms have theoretical guarantees applying across all differentiable games. In this paper we present Stable Opponent Shaping (SOS), a new method that interpolates between LOLA and a stable variant named LookAhead. We prove that LookAhead locally converges and avoids strict saddles in \emph{all differentiable games}, the strongest results in the field so far. SOS inherits these desirable guarantees, while also shaping the learning of opponents and consistently either matching or outperforming LOLA experimentally.