Minimax Theorem for Latent Games or: How I Learned to Stop Worrying about Mixed-Nash and Love Neural Nets
Paper and Code
Feb 14, 2020
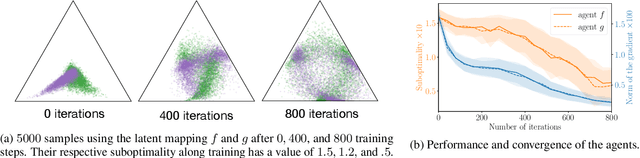
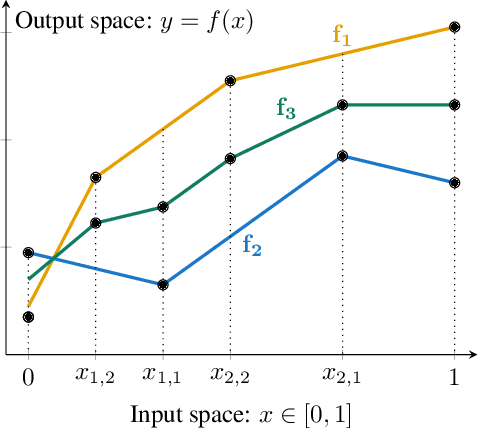
Adversarial training, a special case of multi-objective optimization, is an increasingly useful tool in machine learning. For example, two-player zero-sum games are important for generative modeling (GANs) and for mastering games like Go or Poker via self-play. A classic result in Game Theory states that one must mix strategies, as pure equilibria may not exist. Surprisingly, machine learning practitioners typically train a \emph{single} pair of agents -- instead of a pair of mixtures -- going against Nash's principle. Our main contribution is a notion of limited-capacity-equilibrium for which, as capacity grows, optimal agents -- not mixtures -- can learn increasingly expressive and realistic behaviors. We define \emph{latent games}, a new class of game where agents are mappings that transform latent distributions. Examples include generators in GANs, which transform Gaussian noise into distributions on images, and StarCraft II agents, which transform sampled build orders into policies. We show that minimax equilibria in latent games can be approximated by a \emph{single} pair of dense neural networks. Finally, we apply our latent game approach to solve differentiable Blotto, a game with an infinite strategy space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge