Conditional Approximate Normalizing Flows for Joint Multi-Step Probabilistic Forecasting with Application to Electricity Demand

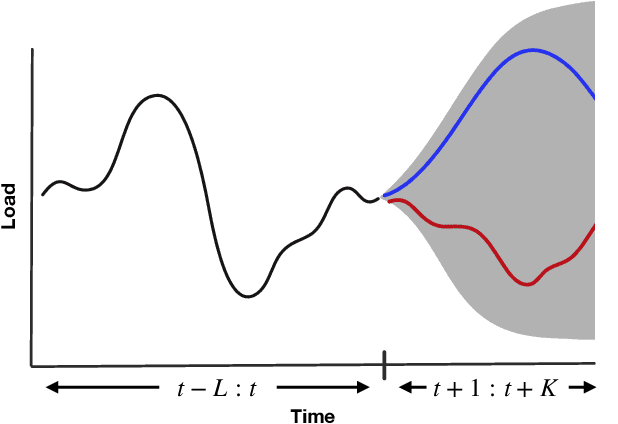
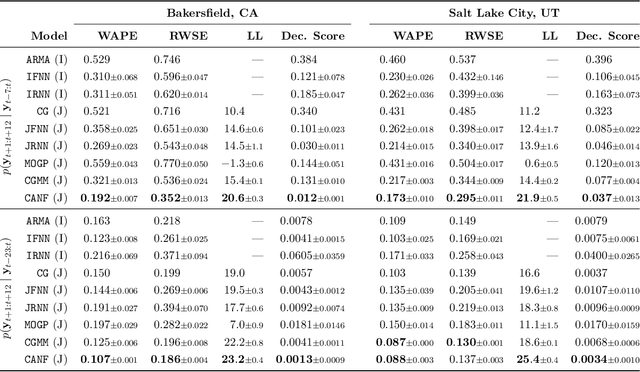
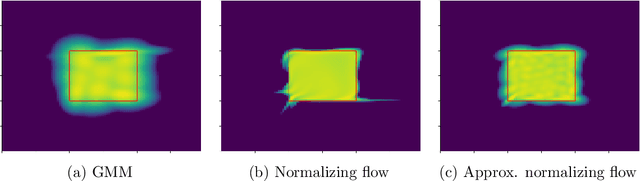
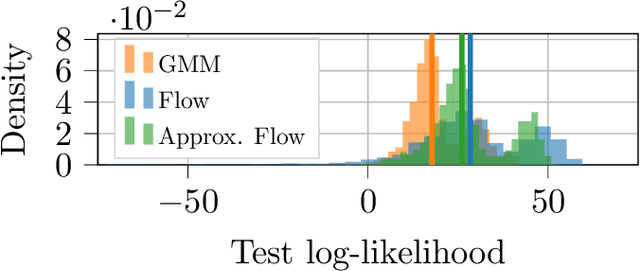
Some real-world decision-making problems require making probabilistic forecasts over multiple steps at once. However, methods for probabilistic forecasting may fail to capture correlations in the underlying time-series that exist over long time horizons as errors accumulate. One such application is with resource scheduling under uncertainty in a grid environment, which requires forecasting electricity demand that is inherently noisy, but often cyclic. In this paper, we introduce the conditional approximate normalizing flow (CANF) to make probabilistic multi-step time-series forecasts when correlations are present over long time horizons. We first demonstrate our method's efficacy on estimating the density of a toy distribution, finding that CANF improves the KL divergence by one-third compared to that of a Gaussian mixture model while still being amenable to explicit conditioning. We then use a publicly available household electricity consumption dataset to showcase the effectiveness of CANF on joint probabilistic multi-step forecasting. Empirical results show that conditional approximate normalizing flows outperform other methods in terms of multi-step forecast accuracy and lead to up to 10x better scheduling decisions. Our implementation is available at https://github.com/sisl/JointDemandForecasting.

Multi-Vehicle Control in Roundabouts using Decentralized Game-Theoretic Planning

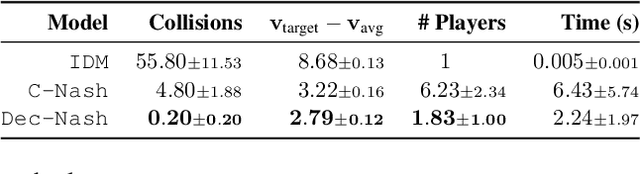
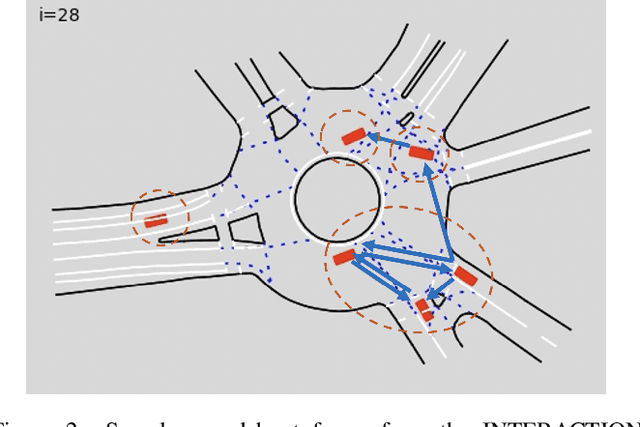
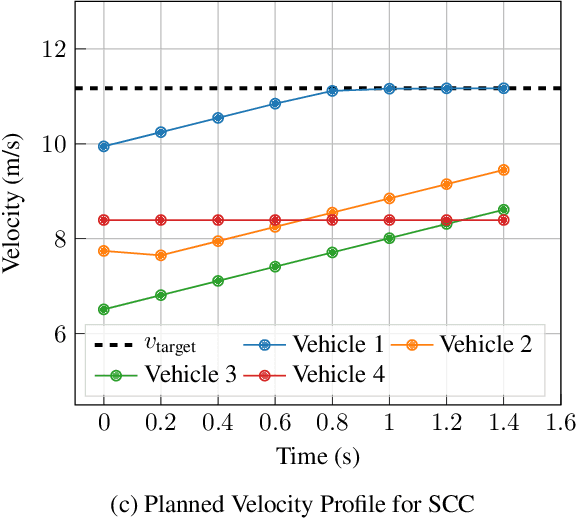
Safe navigation in dense, urban driving environments remains an open problem and an active area of research. Unlike typical predict-then-plan approaches, game-theoretic planning considers how one vehicle's plan will affect the actions of another. Recent work has demonstrated significant improvements in the time required to find local Nash equilibria in general-sum games with nonlinear objectives and constraints. When applied trivially to driving, these works assume all vehicles in a scene play a game together, which can result in intractable computation times for dense traffic. We formulate a decentralized approach to game-theoretic planning by assuming that agents only play games within their observational vicinity, which we believe to be a more reasonable assumption for human driving. Games are played in parallel for all strongly connected components of an interaction graph, significantly reducing the number of players and constraints in each game, and therefore the time required for planning. We demonstrate that our approach can achieve collision-free, efficient driving in urban environments by comparing performance against an adaptation of the Intelligent Driver Model and centralized game-theoretic planning when navigating roundabouts in the INTERACTION dataset. Our implementation is available at http://github.com/sisl/DecNashPlanning.

Training Structured Mechanical Models by Minimizing Discrete Euler-Lagrange Residual

Model-based paradigms for decision-making and control are becoming ubiquitous in robotics. They rely on the ability to efficiently learn a model of the system from data. Structured Mechanical Models (SMMs) are a data-efficient black-box parameterization of mechanical systems, typically fit to data by minimizing the error between predicted and observed accelerations or next states. In this work, we propose a methodology for fitting SMMs to data by minimizing the discrete Euler-Lagrange residual. To study our methodology, we fit models to joint-angle time-series from undamped and damped double-pendulums, studying the quality of learned models fit to data with and without observation noise. Experiments show that our methodology learns models that are better in accuracy to those of the conventional schemes for fitting SMMs. We identify use cases in which our method is a more appropriate methodology. Source code for reproducing the experiments is available at https://github.com/sisl/delsmm.

Scalable Identification of Partially Observed Systems with Certainty-Equivalent EM

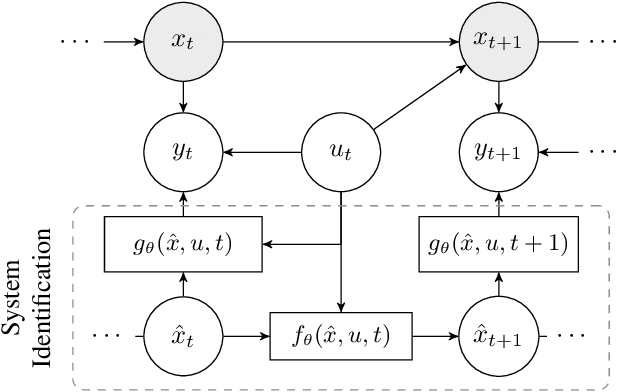
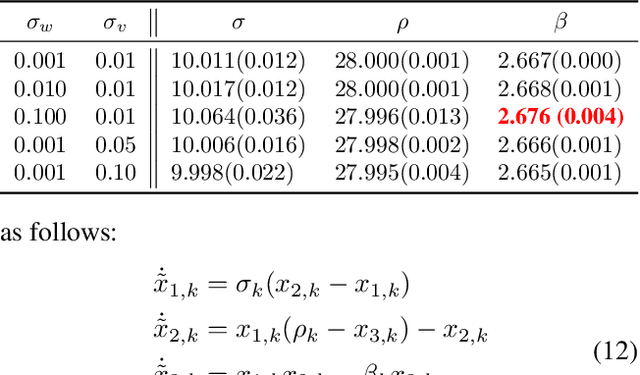
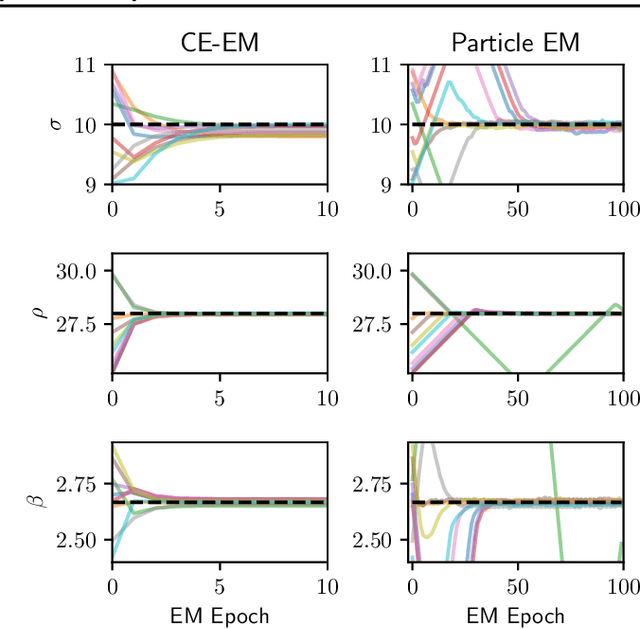
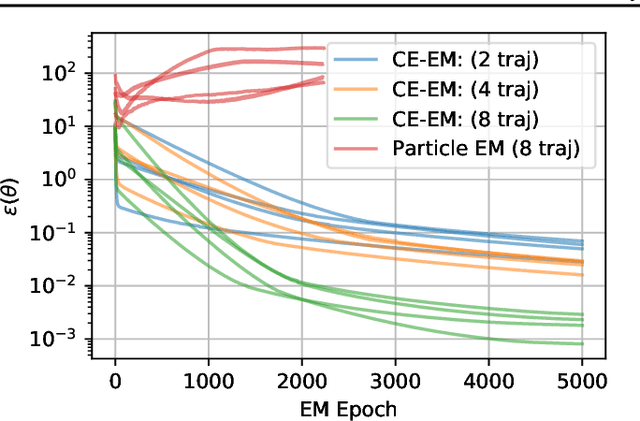
System identification is a key step for model-based control, estimator design, and output prediction. This work considers the offline identification of partially observed nonlinear systems. We empirically show that the certainty-equivalent approximation to expectation-maximization can be a reliable and scalable approach for high-dimensional deterministic systems, which are common in robotics. We formulate certainty-equivalent expectation-maximization as block coordinate-ascent, and provide an efficient implementation. The algorithm is tested on a simulated system of coupled Lorenz attractors, demonstrating its ability to identify high-dimensional systems that can be intractable for particle-based approaches. Our approach is also used to identify the dynamics of an aerobatic helicopter. By augmenting the state with unobserved fluid states, a model is learned that predicts the acceleration of the helicopter better than state-of-the-art approaches. The codebase for this work is available at https://github.com/sisl/CEEM.

Structured Mechanical Models for Robot Learning and Control

Model-based methods are the dominant paradigm for controlling robotic systems, though their efficacy depends heavily on the accuracy of the model used. Deep neural networks have been used to learn models of robot dynamics from data, but they suffer from data-inefficiency and the difficulty to incorporate prior knowledge. We introduce Structured Mechanical Models, a flexible model class for mechanical systems that are data-efficient, easily amenable to prior knowledge, and easily usable with model-based control techniques. The goal of this work is to demonstrate the benefits of using Structured Mechanical Models in lieu of black-box neural networks when modeling robot dynamics. We demonstrate that they generalize better from limited data and yield more reliable model-based controllers on a variety of simulated robotic domains.

A General Framework for Structured Learning of Mechanical Systems

Learning accurate dynamics models is necessary for optimal, compliant control of robotic systems. Current approaches to white-box modeling using analytic parameterizations, or black-box modeling using neural networks, can suffer from high bias or high variance. We address the need for a flexible, gray-box model of mechanical systems that can seamlessly incorporate prior knowledge where it is available, and train expressive function approximators where it is not. We propose to parameterize a mechanical system using neural networks to model its Lagrangian and the generalized forces that act on it. We test our method on a simulated, actuated double pendulum. We show that our method outperforms a naive, black-box model in terms of data-efficiency, as well as performance in model-based reinforcement learning. We also conduct a systematic study of our method's ability to incorporate available prior knowledge about the system to improve data efficiency.

EnsembleDAgger: A Bayesian Approach to Safe Imitation Learning

While imitation learning is often used in robotics, this approach often suffers from data mismatch and compounding errors. DAgger is an iterative algorithm that addresses these issues by aggregating training data from both the expert and novice policies, but does not consider the impact of safety. We present a probabilistic extension to DAgger, which attempts to quantify the confidence of the novice policy as a proxy for safety. Our method, EnsembleDAgger, approximates a GP using an ensemble of neural networks. Using the variance as a measure of confidence, we compute a decision rule that captures how much we doubt the novice, thus determining when it is safe to allow the novice to act. With this approach, we aim to maximize the novice's share of actions, while constraining the probability of failure. We demonstrate improved safety and learning performance compared to other DAgger variants and classic imitation learning on an inverted pendulum and in the MuJoCo HalfCheetah environment.

Deep Reinforcement Learning for Event-Driven Multi-Agent Decision Processes

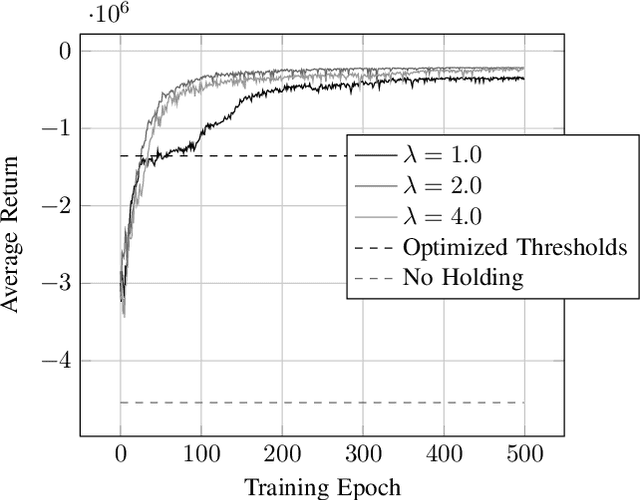
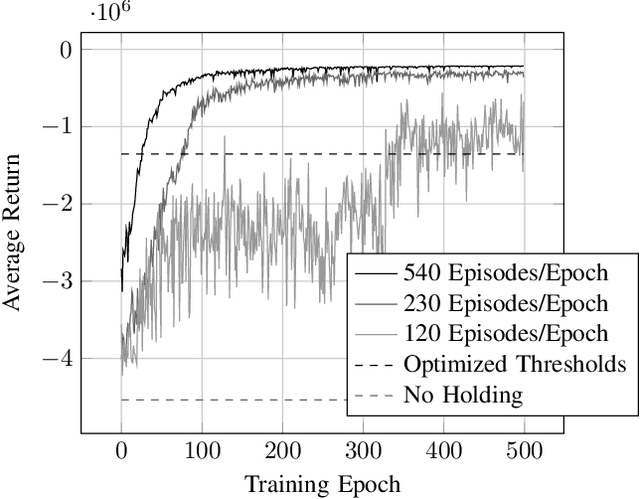
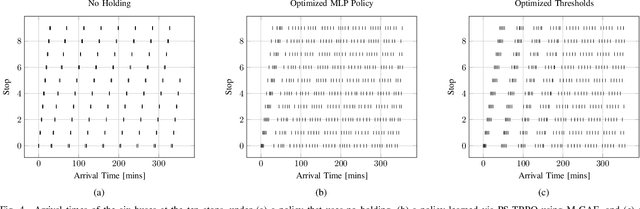
The incorporation of macro-actions (temporally extended actions) into multi-agent decision problems has the potential to address the curse of dimensionality associated with such decision problems. Since macro-actions last for stochastic durations, multiple agents executing decentralized policies in cooperative environments must act asynchronously. We present an algorithm that modifies Generalized Advantage Estimation for temporally extended actions, allowing a state-of-the-art policy optimization algorithm to optimize policies in Dec-POMDPs in which agents act asynchronously. We show that our algorithm is capable of learning optimal policies in two cooperative domains, one involving real-time bus holding control and one involving wildfire fighting with unmanned aircraft. Our algorithm works by framing problems as "event-driven decision processes," which are scenarios where the sequence and timing of actions and events are random and governed by an underlying stochastic process. In addition to optimizing policies with continuous state and action spaces, our algorithm also facilitates the use of event-driven simulators, which do not require time to be discretized into time-steps. We demonstrate the benefit of using event-driven simulation in the context of multiple agents taking asynchronous actions. We show that fixed time-step simulation risks obfuscating the sequence in which closely-separated events occur, adversely affecting the policies learned. Additionally, we show that arbitrarily shrinking the time-step scales poorly with the number of agents.

DropoutDAgger: A Bayesian Approach to Safe Imitation Learning

While imitation learning is becoming common practice in robotics, this approach often suffers from data mismatch and compounding errors. DAgger is an iterative algorithm that addresses these issues by continually aggregating training data from both the expert and novice policies, but does not consider the impact of safety. We present a probabilistic extension to DAgger, which uses the distribution over actions provided by the novice policy, for a given observation. Our method, which we call DropoutDAgger, uses dropout to train the novice as a Bayesian neural network that provides insight to its confidence. Using the distribution over the novice's actions, we estimate a probabilistic measure of safety with respect to the expert action, tuned to balance exploration and exploitation. The utility of this approach is evaluated on the MuJoCo HalfCheetah and in a simple driving experiment, demonstrating improved performance and safety compared to other DAgger variants and classic imitation learning.