Ilan Kroo
Collaborative Multidisciplinary Design Optimization with Neural Networks
Jun 11, 2021



Abstract:The design of complex engineering systems leads to solving very large optimization problems involving different disciplines. Strategies allowing disciplines to optimize in parallel by providing sub-objectives and splitting the problem into smaller parts, such as Collaborative Optimization, are promising solutions.However, most of them have slow convergence which reduces their practical use. Earlier efforts to fasten convergence by learning surrogate models have not yet succeeded at sufficiently improving the competitiveness of these strategies.This paper shows that, in the case of Collaborative Optimization, faster and more reliable convergence can be obtained by solving an interesting instance of binary classification: on top of the target label, the training data of one of the two classes contains the distance to the decision boundary and its derivative. Leveraging this information, we propose to train a neural network with an asymmetric loss function, a structure that guarantees Lipshitz continuity, and a regularization towards respecting basic distance function properties. The approach is demonstrated on a toy learning example, and then applied to a multidisciplinary aircraft design problem.
Scalable Identification of Partially Observed Systems with Certainty-Equivalent EM
Jun 20, 2020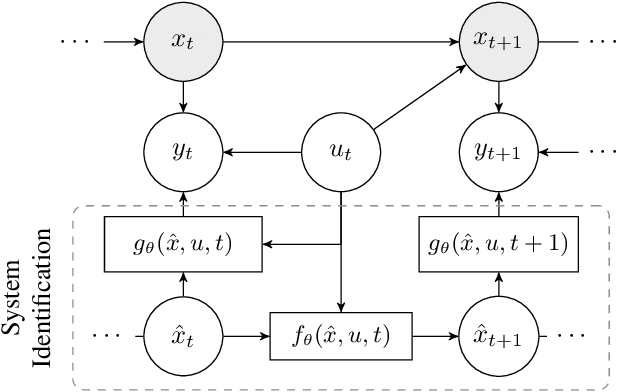
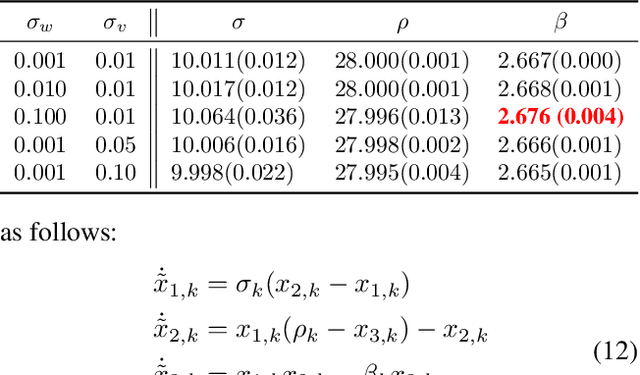
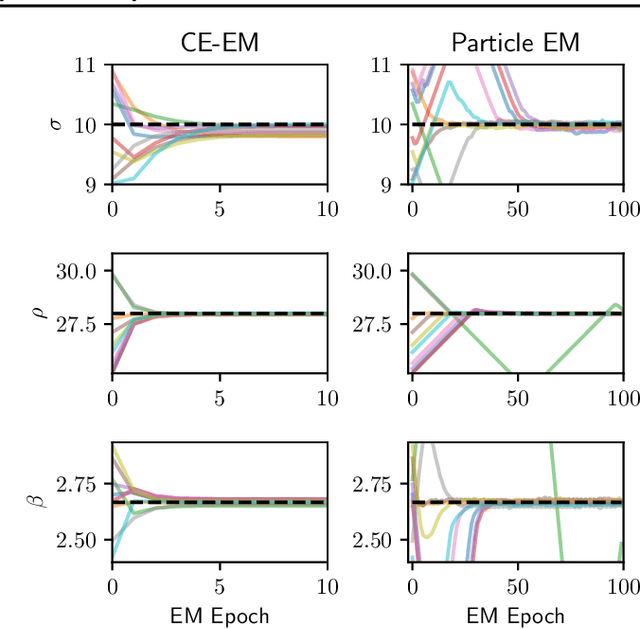
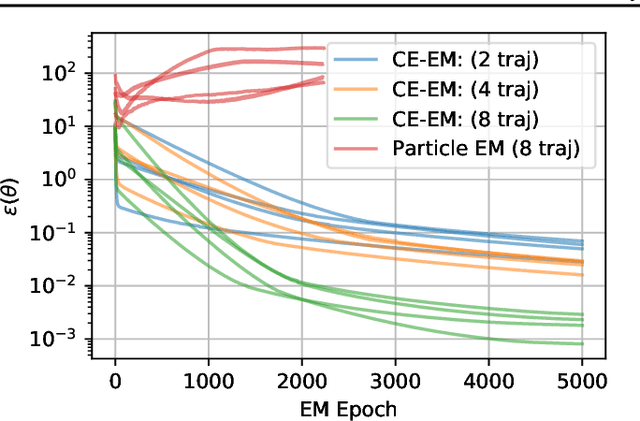
Abstract:System identification is a key step for model-based control, estimator design, and output prediction. This work considers the offline identification of partially observed nonlinear systems. We empirically show that the certainty-equivalent approximation to expectation-maximization can be a reliable and scalable approach for high-dimensional deterministic systems, which are common in robotics. We formulate certainty-equivalent expectation-maximization as block coordinate-ascent, and provide an efficient implementation. The algorithm is tested on a simulated system of coupled Lorenz attractors, demonstrating its ability to identify high-dimensional systems that can be intractable for particle-based approaches. Our approach is also used to identify the dynamics of an aerobatic helicopter. By augmenting the state with unobserved fluid states, a model is learned that predicts the acceleration of the helicopter better than state-of-the-art approaches. The codebase for this work is available at https://github.com/sisl/CEEM.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge