Aurora: A Foundation Model of the Atmosphere

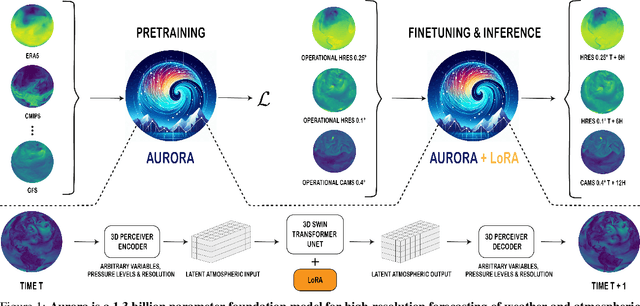
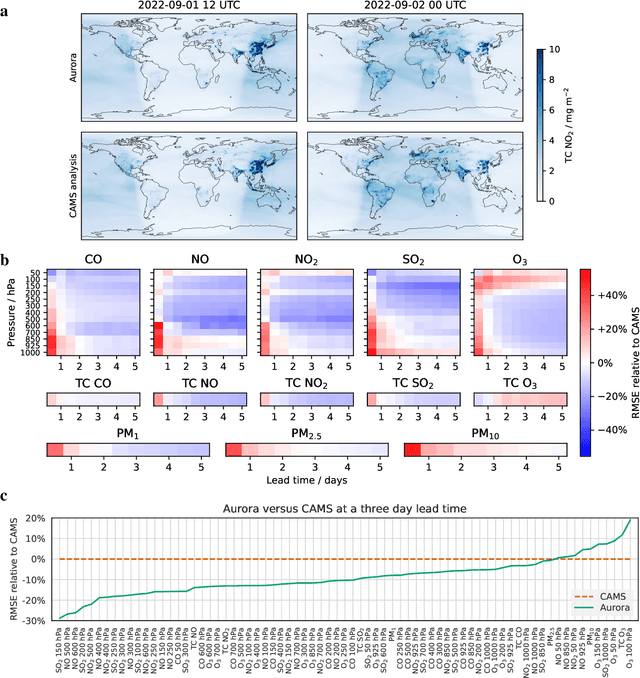
Deep learning foundation models are revolutionizing many facets of science by leveraging vast amounts of data to learn general-purpose representations that can be adapted to tackle diverse downstream tasks. Foundation models hold the promise to also transform our ability to model our planet and its subsystems by exploiting the vast expanse of Earth system data. Here we introduce Aurora, a large-scale foundation model of the atmosphere trained on over a million hours of diverse weather and climate data. Aurora leverages the strengths of the foundation modelling approach to produce operational forecasts for a wide variety of atmospheric prediction problems, including those with limited training data, heterogeneous variables, and extreme events. In under a minute, Aurora produces 5-day global air pollution predictions and 10-day high-resolution weather forecasts that outperform state-of-the-art classical simulation tools and the best specialized deep learning models. Taken together, these results indicate that foundation models can transform environmental forecasting.

EvDNeRF: Reconstructing Event Data with Dynamic Neural Radiance Fields

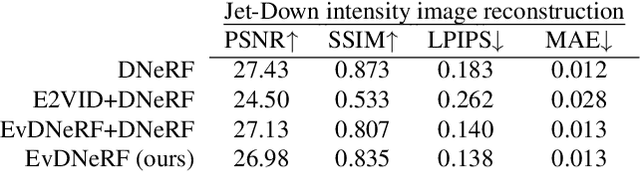
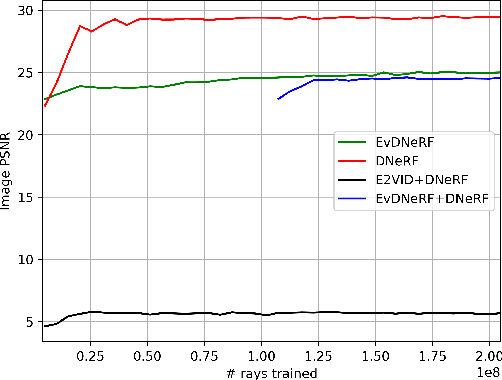
We present EvDNeRF, a pipeline for generating event data and training an event-based dynamic NeRF, for the purpose of faithfully reconstructing eventstreams on scenes with rigid and non-rigid deformations that may be too fast to capture with a standard camera. Event cameras register asynchronous per-pixel brightness changes at MHz rates with high dynamic range, making them ideal for observing fast motion with almost no motion blur. Neural radiance fields (NeRFs) offer visual-quality geometric-based learnable rendering, but prior work with events has only considered reconstruction of static scenes. Our EvDNeRF can predict eventstreams of dynamic scenes from a static or moving viewpoint between any desired timestamps, thereby allowing it to be used as an event-based simulator for a given scene. We show that by training on varied batch sizes of events, we can improve test-time predictions of events at fine time resolutions, outperforming baselines that pair standard dynamic NeRFs with event simulators. We release our simulated and real datasets, as well as code for both event-based data generation and the training of event-based dynamic NeRF models (https://github.com/anish-bhattacharya/EvDNeRF).

Geometric Clifford Algebra Networks

We propose Geometric Clifford Algebra Networks (GCANs) that are based on symmetry group transformations using geometric (Clifford) algebras. GCANs are particularly well-suited for representing and manipulating geometric transformations, often found in dynamical systems. We first review the quintessence of modern (plane-based) geometric algebra, which builds on isometries encoded as elements of the $\mathrm{Pin}(p,q,r)$ group. We then propose the concept of group action layers, which linearly combine object transformations using pre-specified group actions. Together with a new activation and normalization scheme, these layers serve as adjustable geometric templates that can be refined via gradient descent. Theoretical advantages are strongly reflected in the modeling of three-dimensional rigid body transformations as well as large-scale fluid dynamics simulations, showing significantly improved performance over traditional methods.

ClimaX: A foundation model for weather and climate

Most state-of-the-art approaches for weather and climate modeling are based on physics-informed numerical models of the atmosphere. These approaches aim to model the non-linear dynamics and complex interactions between multiple variables, which are challenging to approximate. Additionally, many such numerical models are computationally intensive, especially when modeling the atmospheric phenomenon at a fine-grained spatial and temporal resolution. Recent data-driven approaches based on machine learning instead aim to directly solve a downstream forecasting or projection task by learning a data-driven functional mapping using deep neural networks. However, these networks are trained using curated and homogeneous climate datasets for specific spatiotemporal tasks, and thus lack the generality of numerical models. We develop and demonstrate ClimaX, a flexible and generalizable deep learning model for weather and climate science that can be trained using heterogeneous datasets spanning different variables, spatio-temporal coverage, and physical groundings. ClimaX extends the Transformer architecture with novel encoding and aggregation blocks that allow effective use of available compute while maintaining general utility. ClimaX is pre-trained with a self-supervised learning objective on climate datasets derived from CMIP6. The pre-trained ClimaX can then be fine-tuned to address a breadth of climate and weather tasks, including those that involve atmospheric variables and spatio-temporal scales unseen during pretraining. Compared to existing data-driven baselines, we show that this generality in ClimaX results in superior performance on benchmarks for weather forecasting and climate projections, even when pretrained at lower resolutions and compute budgets.

Agent-Time Attention for Sparse Rewards Multi-Agent Reinforcement Learning

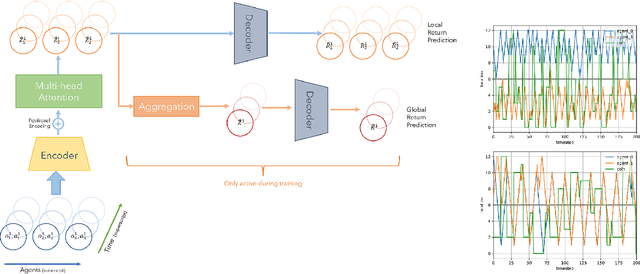
Sparse and delayed rewards pose a challenge to single agent reinforcement learning. This challenge is amplified in multi-agent reinforcement learning (MARL) where credit assignment of these rewards needs to happen not only across time, but also across agents. We propose Agent-Time Attention (ATA), a neural network model with auxiliary losses for redistributing sparse and delayed rewards in collaborative MARL. We provide a simple example that demonstrates how providing agents with their own local redistributed rewards and shared global redistributed rewards motivate different policies. We extend several MiniGrid environments, specifically MultiRoom and DoorKey, to the multi-agent sparse delayed rewards setting. We demonstrate that ATA outperforms various baselines on many instances of these environments. Source code of the experiments is available at https://github.com/jshe/agent-time-attention.

Learning Modular Simulations for Homogeneous Systems

Complex systems are often decomposed into modular subsystems for engineering tractability. Although various equation based white-box modeling techniques make use of such structure, learning based methods have yet to incorporate these ideas broadly. We present a modular simulation framework for modeling homogeneous multibody dynamical systems, which combines ideas from graph neural networks and neural differential equations. We learn to model the individual dynamical subsystem as a neural ODE module. Full simulation of the composite system is orchestrated via spatio-temporal message passing between these modules. An arbitrary number of modules can be combined to simulate systems of a wide variety of coupling topologies. We evaluate our framework on a variety of systems and show that message passing allows coordination between multiple modules over time for accurate predictions and in certain cases, enables zero-shot generalization to new system configurations. Furthermore, we show that our models can be transferred to new system configurations with lower data requirement and training effort, compared to those trained from scratch.

Towards Multi-spatiotemporal-scale Generalized PDE Modeling

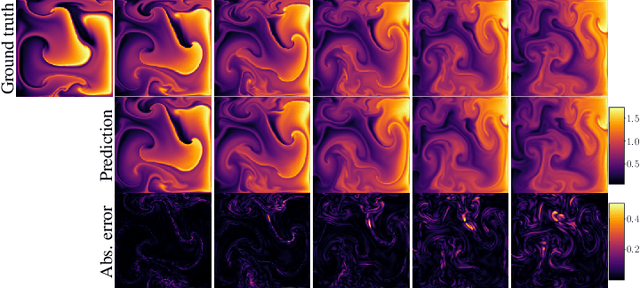
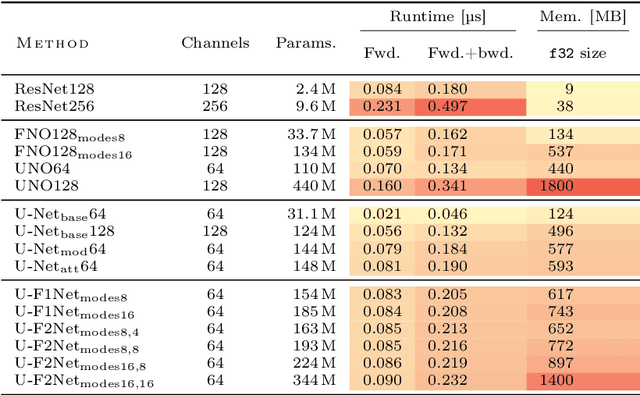
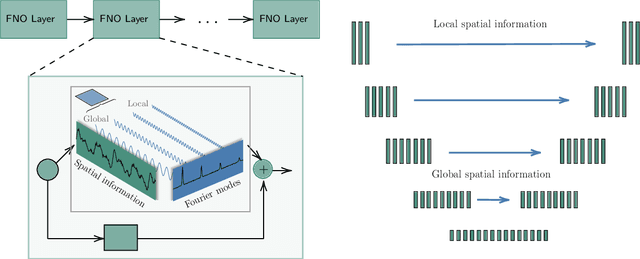
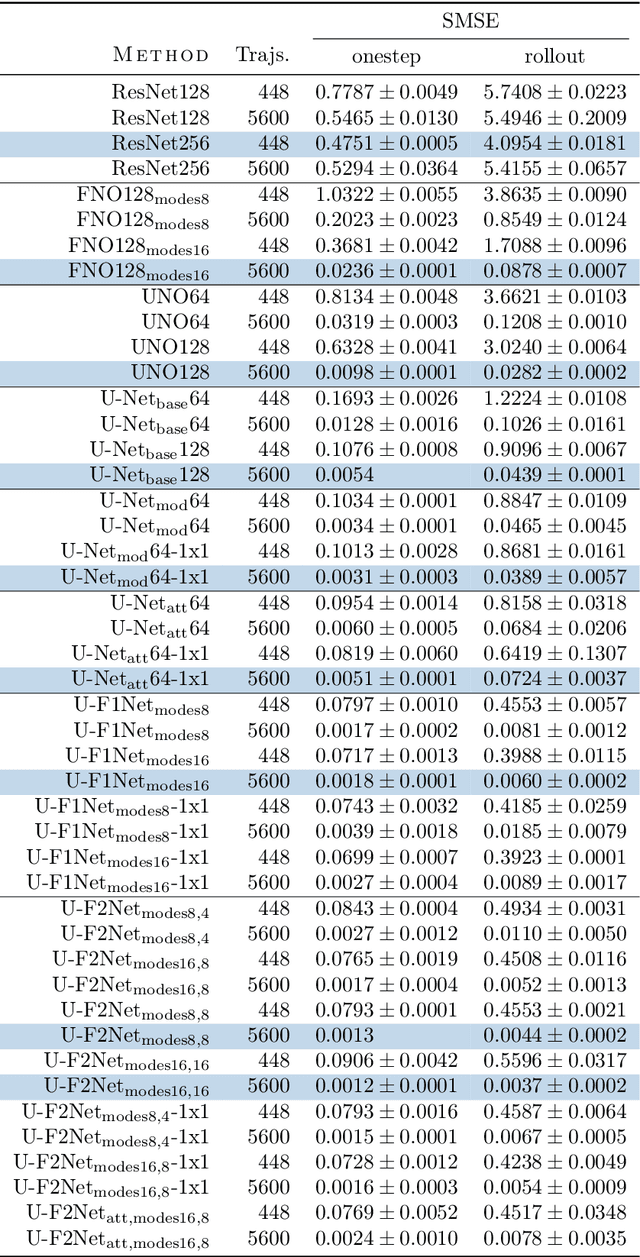
Partial differential equations (PDEs) are central to describing complex physical system simulations. Their expensive solution techniques have led to an increased interest in deep neural network based surrogates. However, the practical utility of training such surrogates is contingent on their ability to model complex multi-scale spatio-temporal phenomena. Various neural network architectures have been proposed to target such phenomena, most notably Fourier Neural Operators (FNOs) which give a natural handle over local \& global spatial information via parameterization of different Fourier modes, and U-Nets which treat local and global information via downsampling and upsampling paths. However, generalizing across different equation parameters or different time-scales still remains a challenge. In this work, we make a comprehensive comparison between various FNO and U-Net like approaches on fluid mechanics problems in both vorticity-stream and velocity function form. For U-Nets, we transfer recent architectural improvements from computer vision, most notably from object segmentation and generative modeling. We further analyze the design considerations for using FNO layers to improve performance of U-Net architectures without major degradation of computational performance. Finally, we show promising results on generalization to different PDE parameters and time-scales with a single surrogate model.

Learning to Simulate Realistic LiDARs

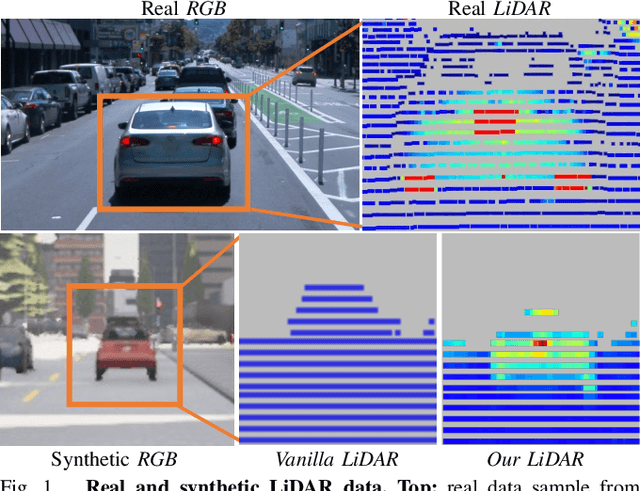
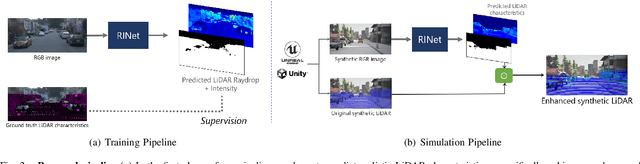
Simulating realistic sensors is a challenging part in data generation for autonomous systems, often involving carefully handcrafted sensor design, scene properties, and physics modeling. To alleviate this, we introduce a pipeline for data-driven simulation of a realistic LiDAR sensor. We propose a model that learns a mapping between RGB images and corresponding LiDAR features such as raydrop or per-point intensities directly from real datasets. We show that our model can learn to encode realistic effects such as dropped points on transparent surfaces or high intensity returns on reflective materials. When applied to naively raycasted point clouds provided by off-the-shelf simulator software, our model enhances the data by predicting intensities and removing points based on the scene's appearance to match a real LiDAR sensor. We use our technique to learn models of two distinct LiDAR sensors and use them to improve simulated LiDAR data accordingly. Through a sample task of vehicle segmentation, we show that enhancing simulated point clouds with our technique improves downstream task performance.

Clifford Neural Layers for PDE Modeling

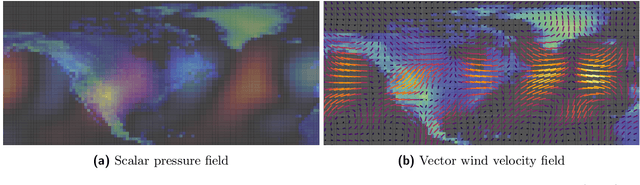
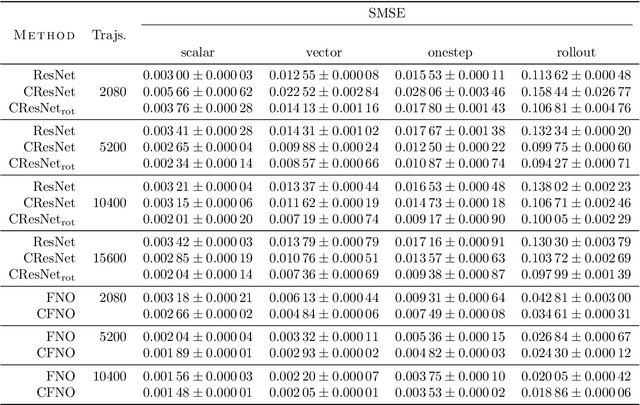
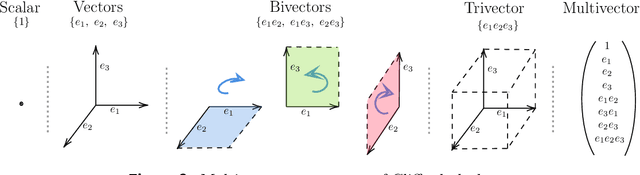
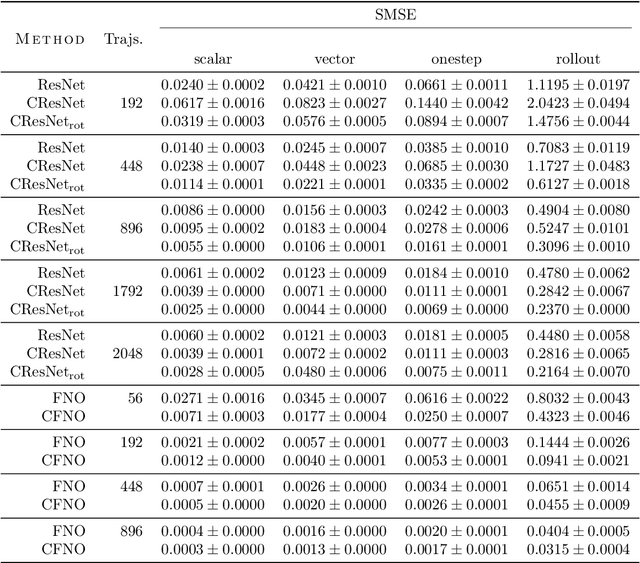
Partial differential equations (PDEs) see widespread use in sciences and engineering to describe simulation of physical processes as scalar and vector fields interacting and coevolving over time. Due to the computationally expensive nature of their standard solution methods, neural PDE surrogates have become an active research topic to accelerate these simulations. However, current methods do not explicitly take into account the relationship between different fields and their internal components, which are often correlated. Viewing the time evolution of such correlated fields through the lens of multivector fields allows us to overcome these limitations. Multivector fields consist of scalar, vector, as well as higher-order components, such as bivectors and trivectors. Their algebraic properties, such as multiplication, addition and other arithmetic operations can be described by Clifford algebras. To our knowledge, this paper presents the first usage of such multivector representations together with Clifford convolutions and Clifford Fourier transforms in the context of deep learning. The resulting Clifford neural layers are universally applicable and will find direct use in the areas of fluid dynamics, weather forecasting, and the modeling of physical systems in general. We empirically evaluate the benefit of Clifford neural layers by replacing convolution and Fourier operations in common neural PDE surrogates by their Clifford counterparts on two-dimensional Navier-Stokes and weather modeling tasks, as well as three-dimensional Maxwell equations. Clifford neural layers consistently improve generalization capabilities of the tested neural PDE surrogates.

Recursive Reasoning Graph for Multi-Agent Reinforcement Learning

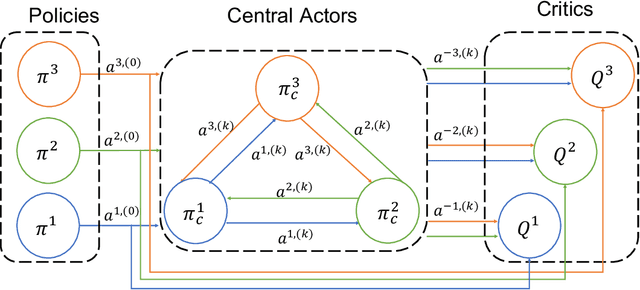
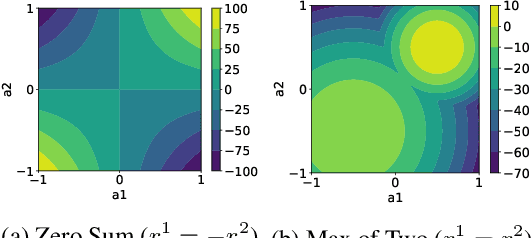
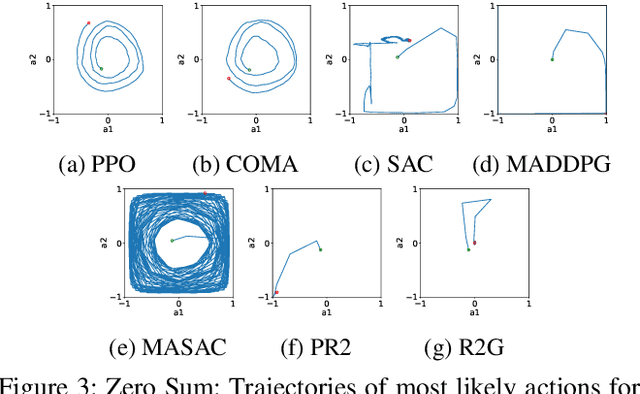
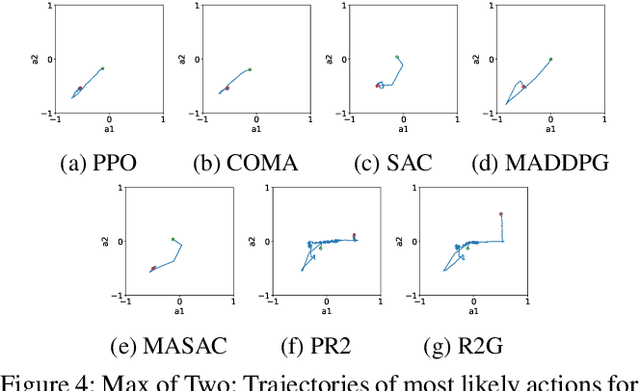
Multi-agent reinforcement learning (MARL) provides an efficient way for simultaneously learning policies for multiple agents interacting with each other. However, in scenarios requiring complex interactions, existing algorithms can suffer from an inability to accurately anticipate the influence of self-actions on other agents. Incorporating an ability to reason about other agents' potential responses can allow an agent to formulate more effective strategies. This paper adopts a recursive reasoning model in a centralized-training-decentralized-execution framework to help learning agents better cooperate with or compete against others. The proposed algorithm, referred to as the Recursive Reasoning Graph (R2G), shows state-of-the-art performance on multiple multi-agent particle and robotics games.