Towards Multi-spatiotemporal-scale Generalized PDE Modeling

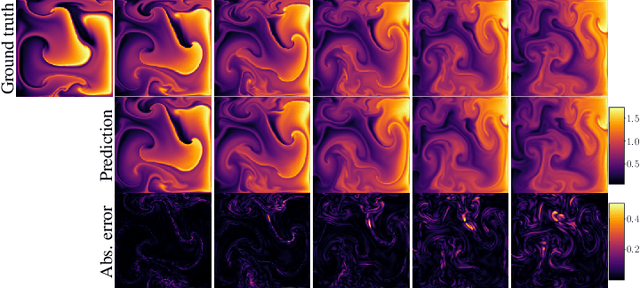
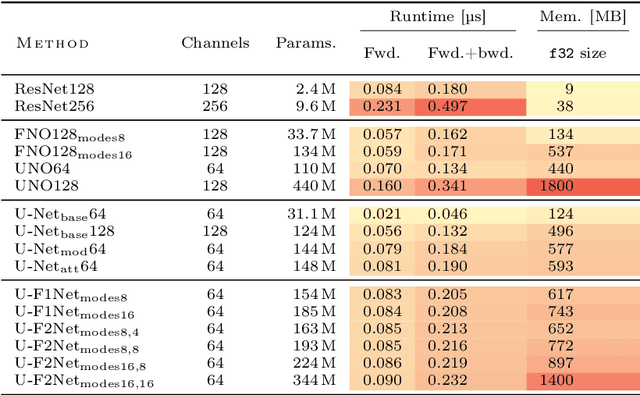
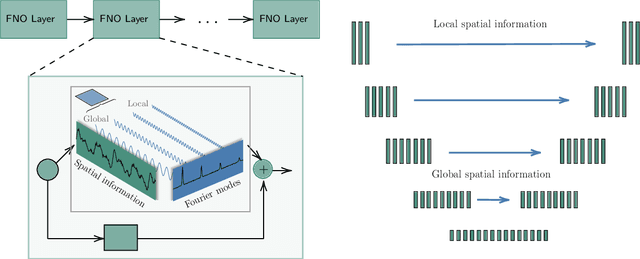
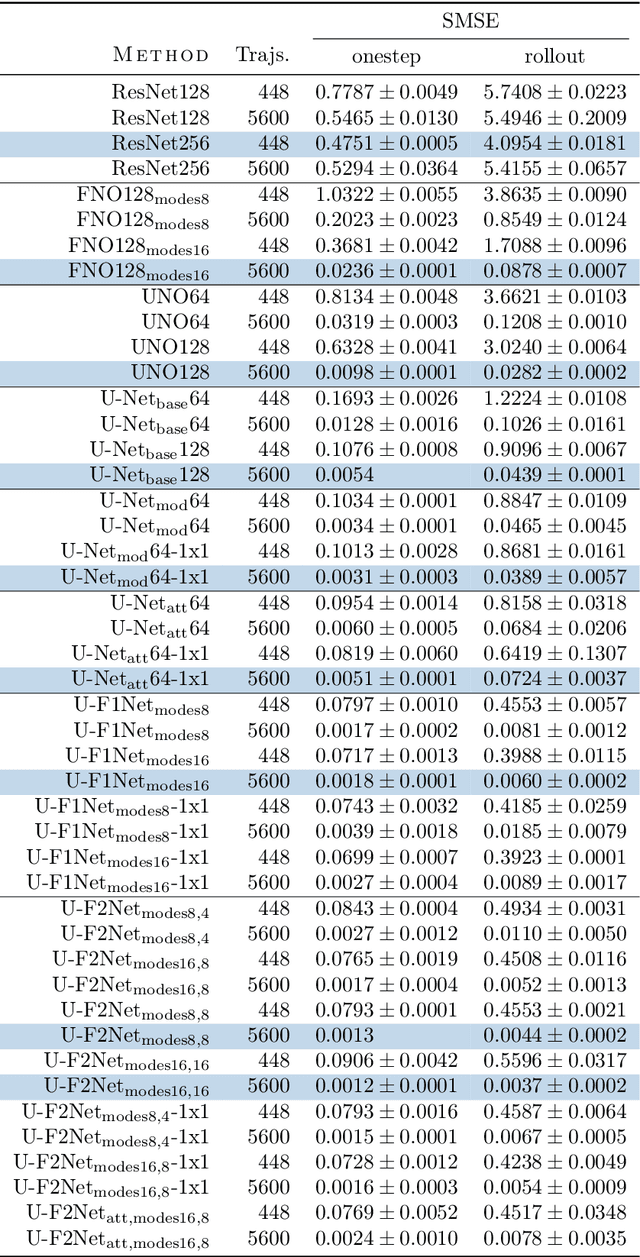
Partial differential equations (PDEs) are central to describing complex physical system simulations. Their expensive solution techniques have led to an increased interest in deep neural network based surrogates. However, the practical utility of training such surrogates is contingent on their ability to model complex multi-scale spatio-temporal phenomena. Various neural network architectures have been proposed to target such phenomena, most notably Fourier Neural Operators (FNOs) which give a natural handle over local \& global spatial information via parameterization of different Fourier modes, and U-Nets which treat local and global information via downsampling and upsampling paths. However, generalizing across different equation parameters or different time-scales still remains a challenge. In this work, we make a comprehensive comparison between various FNO and U-Net like approaches on fluid mechanics problems in both vorticity-stream and velocity function form. For U-Nets, we transfer recent architectural improvements from computer vision, most notably from object segmentation and generative modeling. We further analyze the design considerations for using FNO layers to improve performance of U-Net architectures without major degradation of computational performance. Finally, we show promising results on generalization to different PDE parameters and time-scales with a single surrogate model.