Two for One: Diffusion Models and Force Fields for Coarse-Grained Molecular Dynamics

Coarse-grained (CG) molecular dynamics enables the study of biological processes at temporal and spatial scales that would be intractable at an atomistic resolution. However, accurately learning a CG force field remains a challenge. In this work, we leverage connections between score-based generative models, force fields and molecular dynamics to learn a CG force field without requiring any force inputs during training. Specifically, we train a diffusion generative model on protein structures from molecular dynamics simulations, and we show that its score function approximates a force field that can directly be used to simulate CG molecular dynamics. While having a vastly simplified training setup compared to previous work, we demonstrate that our approach leads to improved performance across several small- to medium-sized protein simulations, reproducing the CG equilibrium distribution, and preserving dynamics of all-atom simulations such as protein folding events.

Protein structure generation via folding diffusion

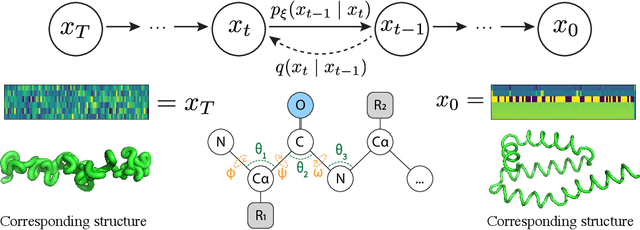
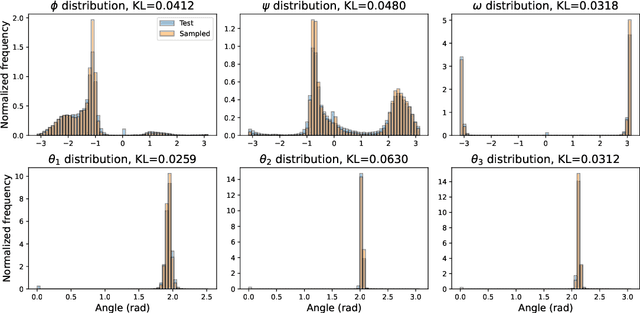
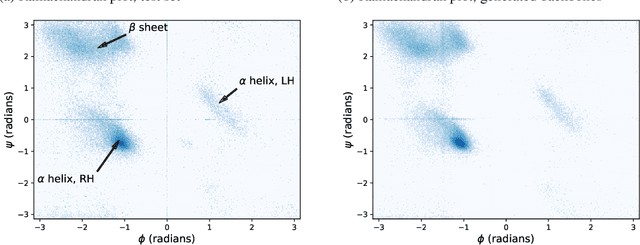
The ability to computationally generate novel yet physically foldable protein structures could lead to new biological discoveries and new treatments targeting yet incurable diseases. Despite recent advances in protein structure prediction, directly generating diverse, novel protein structures from neural networks remains difficult. In this work, we present a new diffusion-based generative model that designs protein backbone structures via a procedure that mirrors the native folding process. We describe protein backbone structure as a series of consecutive angles capturing the relative orientation of the constituent amino acid residues, and generate new structures by denoising from a random, unfolded state towards a stable folded structure. Not only does this mirror how proteins biologically twist into energetically favorable conformations, the inherent shift and rotational invariance of this representation crucially alleviates the need for complex equivariant networks. We train a denoising diffusion probabilistic model with a simple transformer backbone and demonstrate that our resulting model unconditionally generates highly realistic protein structures with complexity and structural patterns akin to those of naturally-occurring proteins. As a useful resource, we release the first open-source codebase and trained models for protein structure diffusion.

Clifford Neural Layers for PDE Modeling

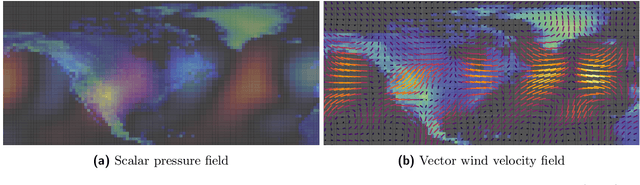
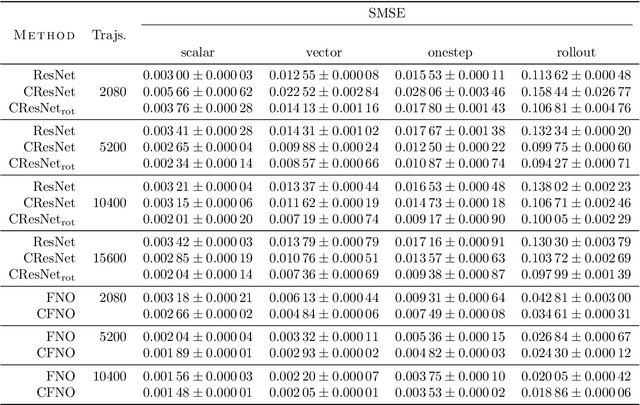
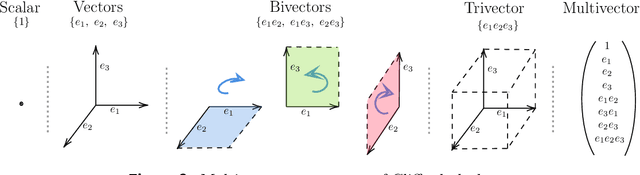
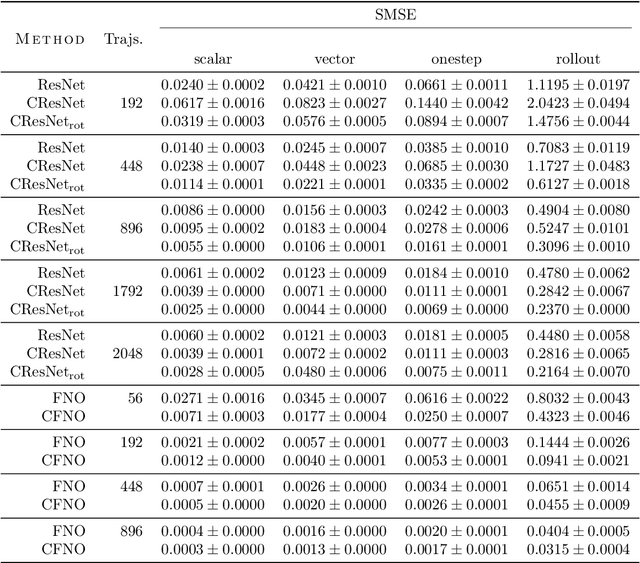
Partial differential equations (PDEs) see widespread use in sciences and engineering to describe simulation of physical processes as scalar and vector fields interacting and coevolving over time. Due to the computationally expensive nature of their standard solution methods, neural PDE surrogates have become an active research topic to accelerate these simulations. However, current methods do not explicitly take into account the relationship between different fields and their internal components, which are often correlated. Viewing the time evolution of such correlated fields through the lens of multivector fields allows us to overcome these limitations. Multivector fields consist of scalar, vector, as well as higher-order components, such as bivectors and trivectors. Their algebraic properties, such as multiplication, addition and other arithmetic operations can be described by Clifford algebras. To our knowledge, this paper presents the first usage of such multivector representations together with Clifford convolutions and Clifford Fourier transforms in the context of deep learning. The resulting Clifford neural layers are universally applicable and will find direct use in the areas of fluid dynamics, weather forecasting, and the modeling of physical systems in general. We empirically evaluate the benefit of Clifford neural layers by replacing convolution and Fourier operations in common neural PDE surrogates by their Clifford counterparts on two-dimensional Navier-Stokes and weather modeling tasks, as well as three-dimensional Maxwell equations. Clifford neural layers consistently improve generalization capabilities of the tested neural PDE surrogates.

Autoregressive Diffusion Models

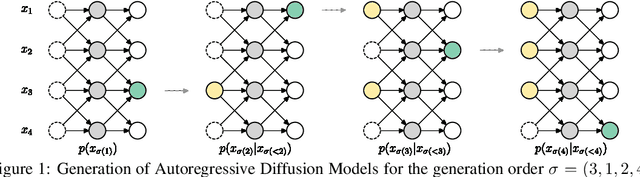
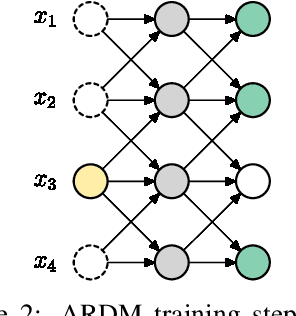
We introduce Autoregressive Diffusion Models (ARDMs), a model class encompassing and generalizing order-agnostic autoregressive models (Uria et al., 2014) and absorbing discrete diffusion (Austin et al., 2021), which we show are special cases of ARDMs under mild assumptions. ARDMs are simple to implement and easy to train. Unlike standard ARMs, they do not require causal masking of model representations, and can be trained using an efficient objective similar to modern probabilistic diffusion models that scales favourably to highly-dimensional data. At test time, ARDMs support parallel generation which can be adapted to fit any given generation budget. We find that ARDMs require significantly fewer steps than discrete diffusion models to attain the same performance. Finally, we apply ARDMs to lossless compression, and show that they are uniquely suited to this task. Contrary to existing approaches based on bits-back coding, ARDMs obtain compelling results not only on complete datasets, but also on compressing single data points. Moreover, this can be done using a modest number of network calls for (de)compression due to the model's adaptable parallel generation.

Beyond In-Place Corruption: Insertion and Deletion In Denoising Probabilistic Models

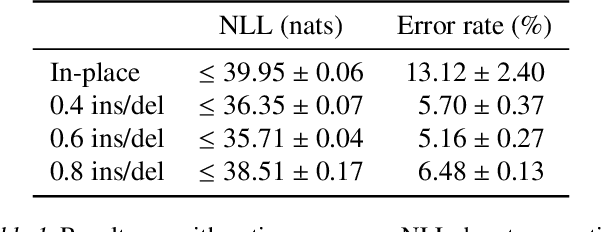
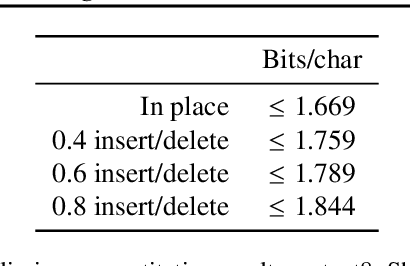
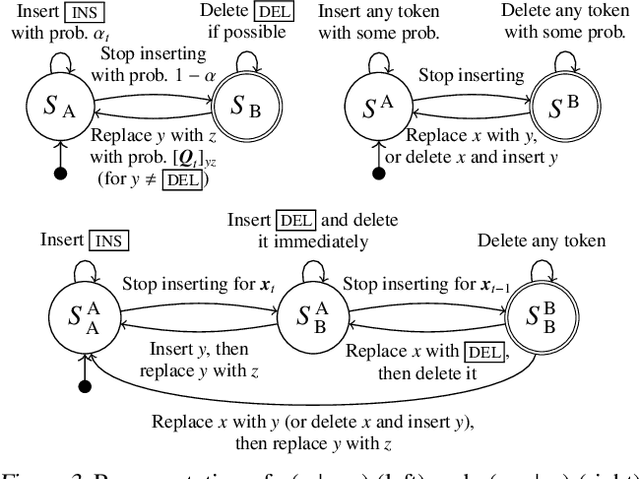
Denoising diffusion probabilistic models (DDPMs) have shown impressive results on sequence generation by iteratively corrupting each example and then learning to map corrupted versions back to the original. However, previous work has largely focused on in-place corruption, adding noise to each pixel or token individually while keeping their locations the same. In this work, we consider a broader class of corruption processes and denoising models over sequence data that can insert and delete elements, while still being efficient to train and sample from. We demonstrate that these models outperform standard in-place models on an arithmetic sequence task, and that when trained on the text8 dataset they can be used to fix spelling errors without any fine-tuning.

Structured Denoising Diffusion Models in Discrete State-Spaces

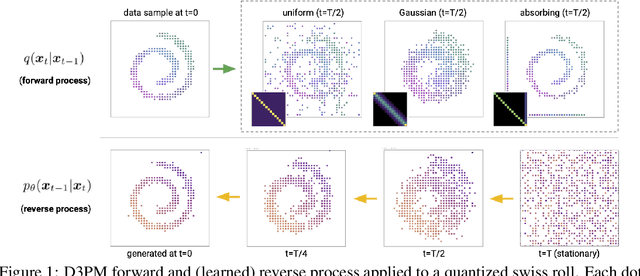
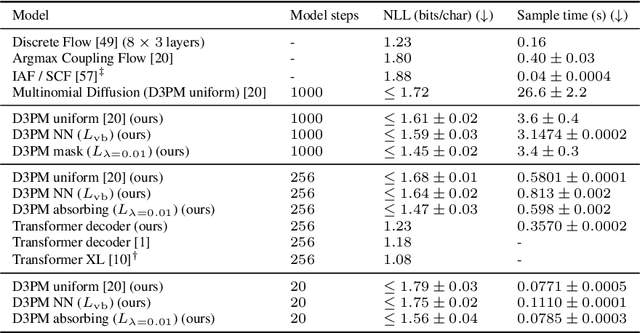
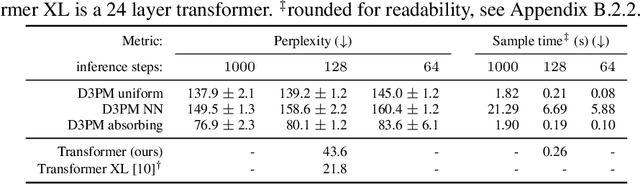
Denoising diffusion probabilistic models (DDPMs) (Ho et al. 2020) have shown impressive results on image and waveform generation in continuous state spaces. Here, we introduce Discrete Denoising Diffusion Probabilistic Models (D3PMs), diffusion-like generative models for discrete data that generalize the multinomial diffusion model of Hoogeboom et al. 2021, by going beyond corruption processes with uniform transition probabilities. This includes corruption with transition matrices that mimic Gaussian kernels in continuous space, matrices based on nearest neighbors in embedding space, and matrices that introduce absorbing states. The third allows us to draw a connection between diffusion models and autoregressive and mask-based generative models. We show that the choice of transition matrix is an important design decision that leads to improved results in image and text domains. We also introduce a new loss function that combines the variational lower bound with an auxiliary cross entropy loss. For text, this model class achieves strong results on character-level text generation while scaling to large vocabularies on LM1B. On the image dataset CIFAR-10, our models approach the sample quality and exceed the log-likelihood of the continuous-space DDPM model.

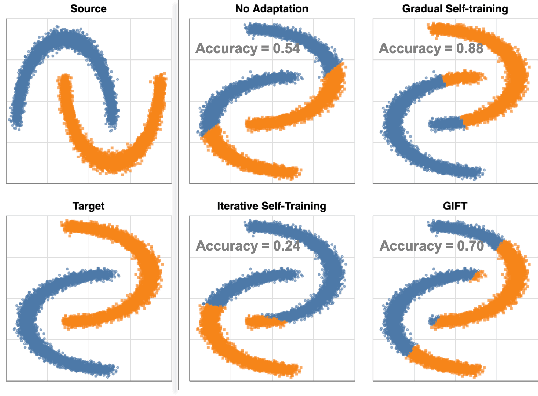
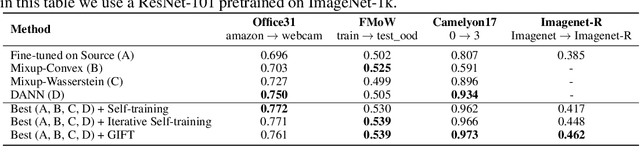
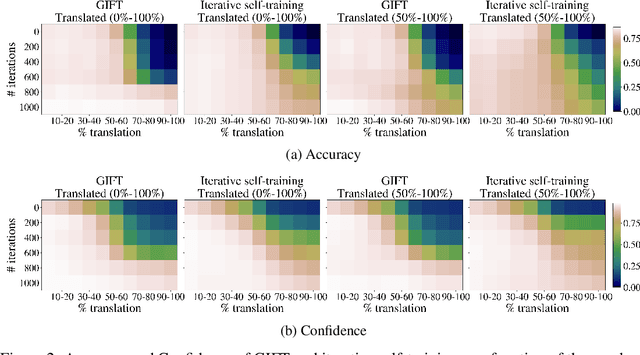
Gradual Domain Adaptation in the Wild:When Intermediate Distributions are Absent

We focus on the problem of domain adaptation when the goal is shifting the model towards the target distribution, rather than learning domain invariant representations. It has been shown that under the following two assumptions: (a) access to samples from intermediate distributions, and (b) samples being annotated with the amount of change from the source distribution, self-training can be successfully applied on gradually shifted samples to adapt the model toward the target distribution. We hypothesize having (a) is enough to enable iterative self-training to slowly adapt the model to the target distribution, by making use of an implicit curriculum. In the case where (a) does not hold, we observe that iterative self-training falls short. We propose GIFT, a method that creates virtual samples from intermediate distributions by interpolating representations of examples from source and target domains. We evaluate an iterative-self-training method on datasets with natural distribution shifts, and show that when applied on top of other domain adaptation methods, it improves the performance of the model on the target dataset. We run an analysis on a synthetic dataset to show that in the presence of (a) iterative-self-training naturally forms a curriculum of samples. Furthermore, we show that when (a) does not hold, GIFT performs better than iterative self-training.

A Spectral Energy Distance for Parallel Speech Synthesis

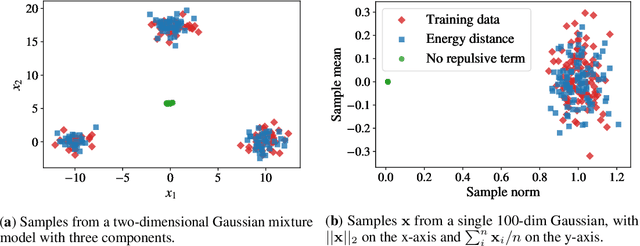
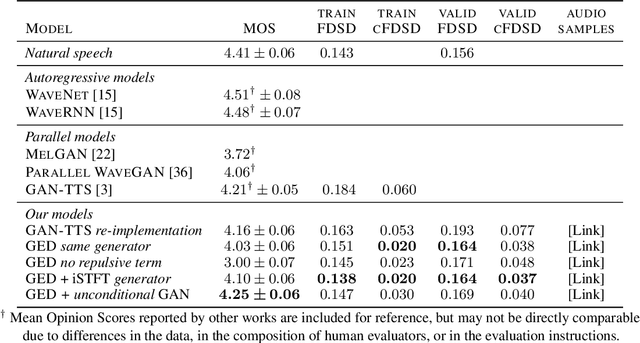
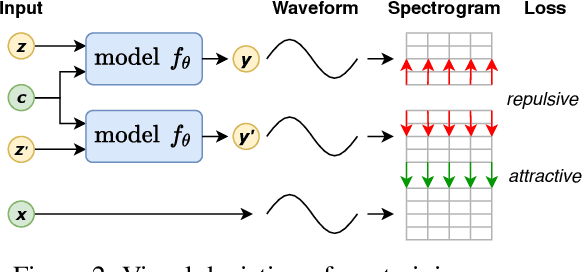
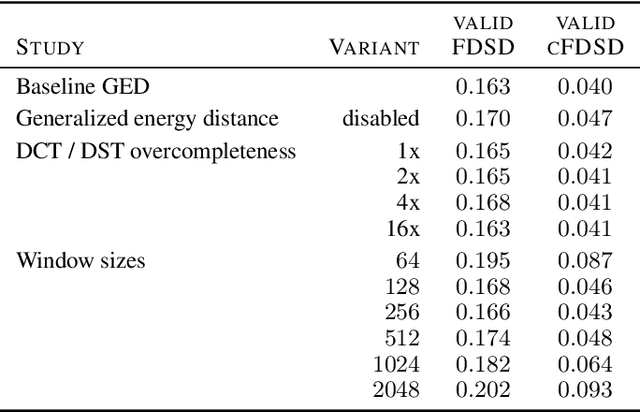
Speech synthesis is an important practical generative modeling problem that has seen great progress over the last few years, with likelihood-based autoregressive neural models now outperforming traditional concatenative systems. A downside of such autoregressive models is that they require executing tens of thousands of sequential operations per second of generated audio, making them ill-suited for deployment on specialized deep learning hardware. Here, we propose a new learning method that allows us to train highly parallel models of speech, without requiring access to an analytical likelihood function. Our approach is based on a generalized energy distance between the distributions of the generated and real audio. This spectral energy distance is a proper scoring rule with respect to the distribution over magnitude-spectrograms of the generated waveform audio and offers statistical consistency guarantees. The distance can be calculated from minibatches without bias, and does not involve adversarial learning, yielding a stable and consistent method for training implicit generative models. Empirically, we achieve state-of-the-art generation quality among implicit generative models, as judged by the recently-proposed cFDSD metric. When combining our method with adversarial techniques, we also improve upon the recently-proposed GAN-TTS model in terms of Mean Opinion Score as judged by trained human evaluators.

IDF++: Analyzing and Improving Integer Discrete Flows for Lossless Compression

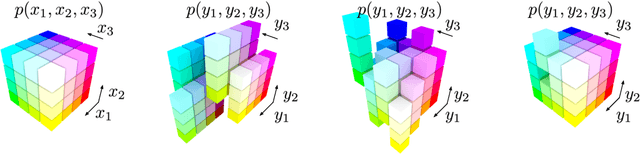
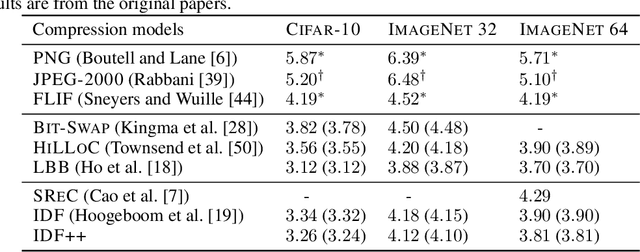
In this paper we analyse and improve integer discrete flows for lossless compression. Integer discrete flows are a recently proposed class of models that learn invertible transformations for integer-valued random variables. Due to its discrete nature, they can be combined in a straightforward manner with entropy coding schemes for lossless compression without the need for bits-back coding. We discuss the potential difference in flexibility between invertible flows for discrete random variables and flows for continuous random variables and show that (integer) discrete flows are more flexible than previously claimed. We furthermore investigate the influence of quantization operators on optimization and gradient bias in integer discrete flows. Finally, we introduce modifications to the architecture to improve the performance of this model class for lossless compression.

Differentiable probabilistic models of scientific imaging with the Fourier slice theorem

Scientific imaging techniques such as optical and electron microscopy and computed tomography (CT) scanning are used to study the 3D structure of an object through 2D observations. These observations are related to the original 3D object through orthogonal integral projections. For common 3D reconstruction algorithms, computational efficiency requires the modeling of the 3D structures to take place in Fourier space by applying the Fourier slice theorem. At present, it is unclear how to differentiate through the projection operator, and hence current learning algorithms can not rely on gradient based methods to optimize 3D structure models. In this paper we show how back-propagation through the projection operator in Fourier space can be achieved. We demonstrate the validity of the approach with experiments on 3D reconstruction of proteins. We further extend our approach to learning probabilistic models of 3D objects. This allows us to predict regions of low sampling rates or estimate noise. A higher sample efficiency can be reached by utilizing the learned uncertainties of the 3D structure as an unsupervised estimate of the model fit. Finally, we demonstrate how the reconstruction algorithm can be extended with an amortized inference scheme on unknown attributes such as object pose. Through empirical studies we show that joint inference of the 3D structure and the object pose becomes more difficult when the ground truth object contains more symmetries. Due to the presence of for instance (approximate) rotational symmetries, the pose estimation can easily get stuck in local optima, inhibiting a fine-grained high-quality estimate of the 3D structure.