Improved motif-scaffolding with SE(3) flow matching

Protein design often begins with knowledge of a desired function from a motif which motif-scaffolding aims to construct a functional protein around. Recently, generative models have achieved breakthrough success in designing scaffolds for a diverse range of motifs. However, the generated scaffolds tend to lack structural diversity, which can hinder success in wet-lab validation. In this work, we extend FrameFlow, an SE(3) flow matching model for protein backbone generation, to perform motif-scaffolding with two complementary approaches. The first is motif amortization, in which FrameFlow is trained with the motif as input using a data augmentation strategy. The second is motif guidance, which performs scaffolding using an estimate of the conditional score from FrameFlow, and requires no additional training. Both approaches achieve an equivalent or higher success rate than previous state-of-the-art methods, with 2.5 times more structurally diverse scaffolds. Code: https://github.com/ microsoft/frame-flow.

Two for One: Diffusion Models and Force Fields for Coarse-Grained Molecular Dynamics

Coarse-grained (CG) molecular dynamics enables the study of biological processes at temporal and spatial scales that would be intractable at an atomistic resolution. However, accurately learning a CG force field remains a challenge. In this work, we leverage connections between score-based generative models, force fields and molecular dynamics to learn a CG force field without requiring any force inputs during training. Specifically, we train a diffusion generative model on protein structures from molecular dynamics simulations, and we show that its score function approximates a force field that can directly be used to simulate CG molecular dynamics. While having a vastly simplified training setup compared to previous work, we demonstrate that our approach leads to improved performance across several small- to medium-sized protein simulations, reproducing the CG equilibrium distribution, and preserving dynamics of all-atom simulations such as protein folding events.

Equivariant 3D-Conditional Diffusion Models for Molecular Linker Design

Fragment-based drug discovery has been an effective paradigm in early-stage drug development. An open challenge in this area is designing linkers between disconnected molecular fragments of interest to obtain chemically-relevant candidate drug molecules. In this work, we propose DiffLinker, an E(3)-equivariant 3D-conditional diffusion model for molecular linker design. Given a set of disconnected fragments, our model places missing atoms in between and designs a molecule incorporating all the initial fragments. Unlike previous approaches that are only able to connect pairs of molecular fragments, our method can link an arbitrary number of fragments. Additionally, the model automatically determines the number of atoms in the linker and its attachment points to the input fragments. We demonstrate that DiffLinker outperforms other methods on the standard datasets generating more diverse and synthetically-accessible molecules. Besides, we experimentally test our method in real-world applications, showing that it can successfully generate valid linkers conditioned on target protein pockets.

Equivariant Diffusion for Molecule Generation in 3D

This work introduces a diffusion model for molecule generation in 3D that is equivariant to Euclidean transformations. Our E(3) Equivariant Diffusion Model (EDM) learns to denoise a diffusion process with an equivariant network that jointly operates on both continuous (atom coordinates) and categorical features (atom types). In addition, we provide a probabilistic analysis which admits likelihood computation of molecules using our model. Experimentally, the proposed method significantly outperforms previous 3D molecular generative methods regarding the quality of generated samples and efficiency at training time.

Multivariate Time Series Forecasting with Latent Graph Inference

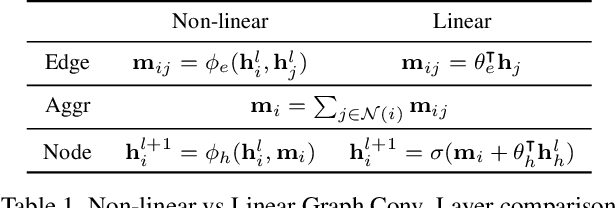
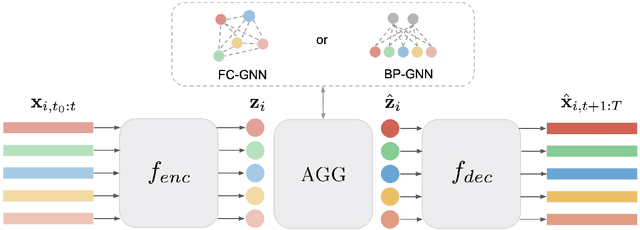
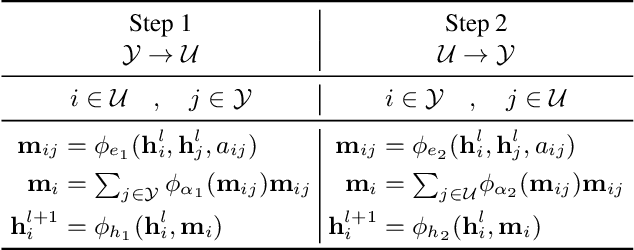
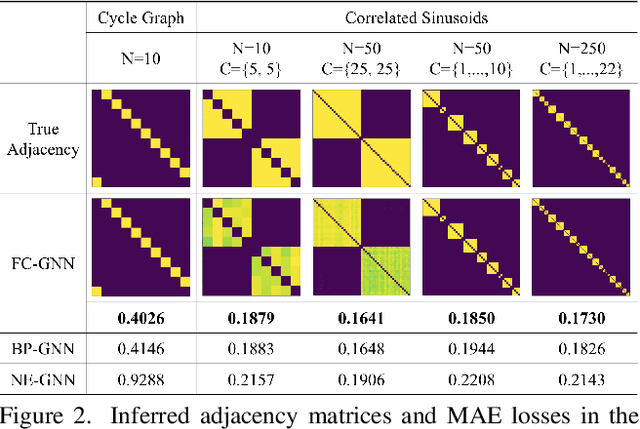
This paper introduces a new approach for Multivariate Time Series forecasting that jointly infers and leverages relations among time series. Its modularity allows it to be integrated with current univariate methods. Our approach allows to trade-off accuracy and computational efficiency gradually via offering on one extreme inference of a potentially fully-connected graph or on another extreme a bipartite graph. In the potentially fully-connected case we consider all pair-wise interactions among time-series which yields the best forecasting accuracy. Conversely, the bipartite case leverages the dependency structure by inter-communicating the N time series through a small set of K auxiliary nodes that we introduce. This reduces the time and memory complexity w.r.t. previous graph inference methods from O(N^2) to O(NK) with a small trade-off in accuracy. We demonstrate the effectiveness of our model in a variety of datasets where both of its variants perform better or very competitively to previous graph inference methods in terms of forecasting accuracy and time efficiency.

A Study of Joint Graph Inference and Forecasting

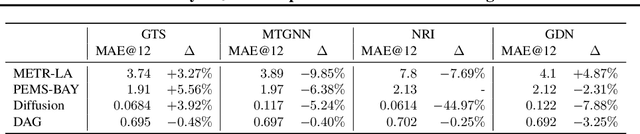
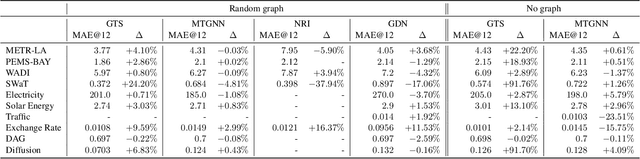
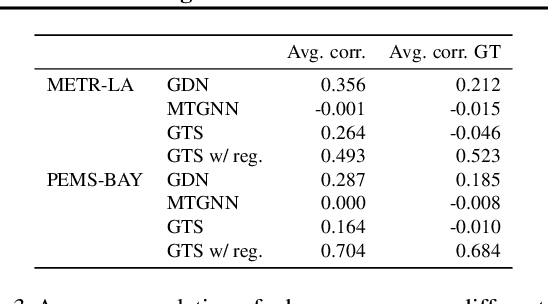
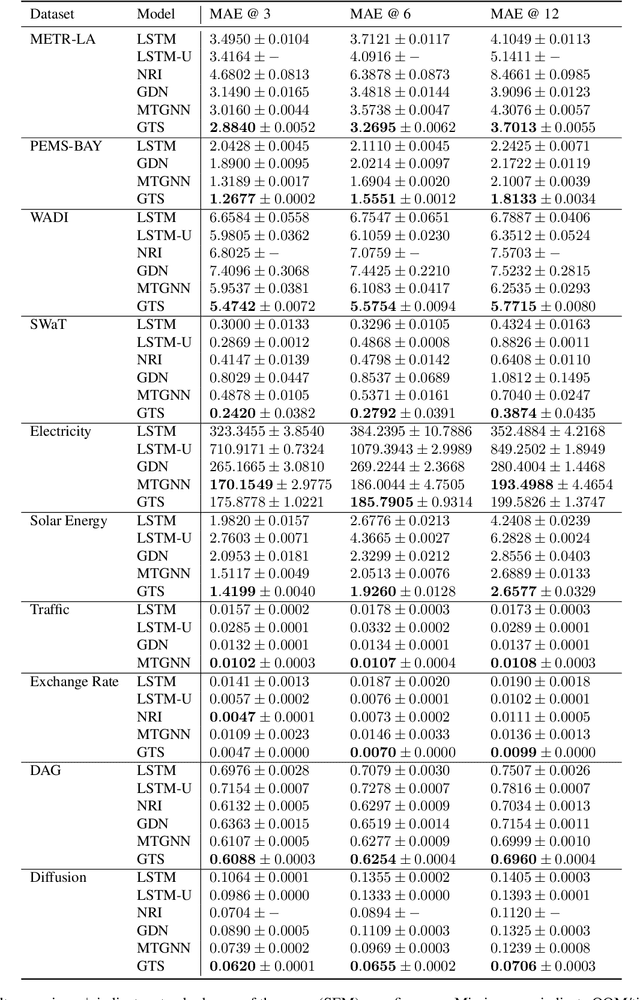
We study a recent class of models which uses graph neural networks (GNNs) to improve forecasting in multivariate time series. The core assumption behind these models is that there is a latent graph between the time series (nodes) that governs the evolution of the multivariate time series. By parameterizing a graph in a differentiable way, the models aim to improve forecasting quality. We compare four recent models of this class on the forecasting task. Further, we perform ablations to study their behavior under changing conditions, e.g., when disabling the graph-learning modules and providing the ground-truth relations instead. Based on our findings, we propose novel ways of combining the existing architectures.

E(n) Equivariant Normalizing Flows

This paper introduces a generative model equivariant to Euclidean symmetries: E(n) Equivariant Normalizing Flows (E-NFs). To construct E-NFs, we take the discriminative E(n) graph neural networks and integrate them as a differential equation to obtain an invertible equivariant function: a continuous-time normalizing flow. We demonstrate that E-NFs considerably outperform baselines and existing methods from the literature on particle systems such as DW4 and LJ13, and on molecules from QM9 in terms of log-likelihood. To the best of our knowledge, this is the first flow that jointly generates molecule features and positions in 3D.

E(n) Equivariant Graph Neural Networks

This paper introduces a new model to learn graph neural networks equivariant to rotations, translations, reflections and permutations called E(n)-Equivariant Graph Neural Networks (EGNNs). In contrast with existing methods, our work does not require computationally expensive higher-order representations in intermediate layers while it still achieves competitive or better performance. In addition, whereas existing methods are limited to equivariance on 3 dimensional spaces, our model is easily scaled to higher-dimensional spaces. We demonstrate the effectiveness of our method on dynamical systems modelling, representation learning in graph autoencoders and predicting molecular properties.

The Convolution Exponential and Generalized Sylvester Flows

This paper introduces a new method to build linear flows, by taking the exponential of a linear transformation. This linear transformation does not need to be invertible itself, and the exponential has the following desirable properties: it is guaranteed to be invertible, its inverse is straightforward to compute and the log Jacobian determinant is equal to the trace of the linear transformation. An important insight is that the exponential can be computed implicitly, which allows the use of convolutional layers. Using this insight, we develop new invertible transformations named convolution exponentials and graph convolution exponentials, which retain the equivariance of their underlying transformations. In addition, we generalize Sylvester Flows and propose Convolutional Sylvester Flows which are based on the generalization and the convolution exponential as basis change. Empirically, we show that the convolution exponential outperforms other linear transformations in generative flows on CIFAR10 and the graph convolution exponential improves the performance of graph normalizing flows. In addition, we show that Convolutional Sylvester Flows improve performance over residual flows as a generative flow model measured in log-likelihood.

Neural Enhanced Belief Propagation on Factor Graphs

A graphical model is a structured representation of locally dependent random variables. A traditional method to reason over these random variables is to perform inference using belief propagation. When provided with the true data generating process, belief propagation can infer the optimal posterior probability estimates in tree structured factor graphs. However, in many cases we may only have access to a poor approximation of the data generating process, or we may face loops in the factor graph, leading to suboptimal estimates. In this work we first extend graph neural networks to factor graphs (FG-GNN). We then propose a new hybrid model that runs conjointly a FG-GNN with belief propagation. The FG-GNN receives as input messages from belief propagation at every inference iteration and outputs a corrected version of them. As a result, we obtain a more accurate algorithm that combines the benefits of both belief propagation and graph neural networks. We apply our ideas to error correction decoding tasks, and we show that our algorithm can outperform belief propagation for LDPC codes on bursty channels.