Chronos: Learning the Language of Time Series

We introduce Chronos, a simple yet effective framework for pretrained probabilistic time series models. Chronos tokenizes time series values using scaling and quantization into a fixed vocabulary and trains existing transformer-based language model architectures on these tokenized time series via the cross-entropy loss. We pretrained Chronos models based on the T5 family (ranging from 20M to 710M parameters) on a large collection of publicly available datasets, complemented by a synthetic dataset that we generated via Gaussian processes to improve generalization. In a comprehensive benchmark consisting of 42 datasets, and comprising both classical local models and deep learning methods, we show that Chronos models: (a) significantly outperform other methods on datasets that were part of the training corpus; and (b) have comparable and occasionally superior zero-shot performance on new datasets, relative to methods that were trained specifically on them. Our results demonstrate that Chronos models can leverage time series data from diverse domains to improve zero-shot accuracy on unseen forecasting tasks, positioning pretrained models as a viable tool to greatly simplify forecasting pipelines.

Deep Non-Parametric Time Series Forecaster

This paper presents non-parametric baseline models for time series forecasting. Unlike classical forecasting models, the proposed approach does not assume any parametric form for the predictive distribution and instead generates predictions by sampling from the empirical distribution according to a tunable strategy. By virtue of this, the model is always able to produce reasonable forecasts (i.e., predictions within the observed data range) without fail unlike classical models that suffer from numerical stability on some data distributions. Moreover, we develop a global version of the proposed method that automatically learns the sampling strategy by exploiting the information across multiple related time series. The empirical evaluation shows that the proposed methods have reasonable and consistent performance across all datasets, proving them to be strong baselines to be considered in one's forecasting toolbox.

Adaptive Sampling for Probabilistic Forecasting under Distribution Shift

The world is not static: This causes real-world time series to change over time through external, and potentially disruptive, events such as macroeconomic cycles or the COVID-19 pandemic. We present an adaptive sampling strategy that selects the part of the time series history that is relevant for forecasting. We achieve this by learning a discrete distribution over relevant time steps by Bayesian optimization. We instantiate this idea with a two-step method that is pre-trained with uniform sampling and then training a lightweight adaptive architecture with adaptive sampling. We show with synthetic and real-world experiments that this method adapts to distribution shift and significantly reduces the forecasting error of the base model for three out of five datasets.

Multivariate Time Series Forecasting with Latent Graph Inference

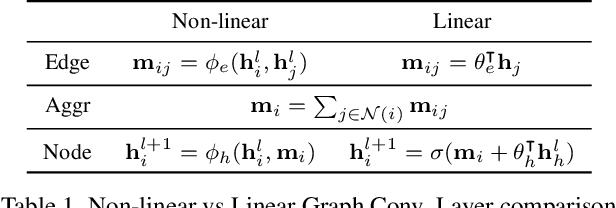
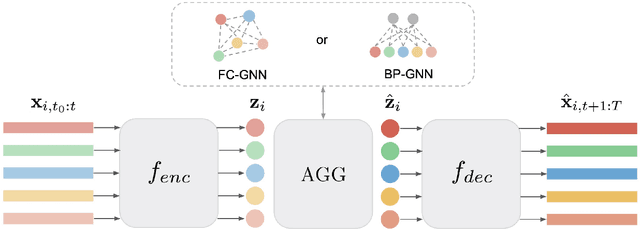
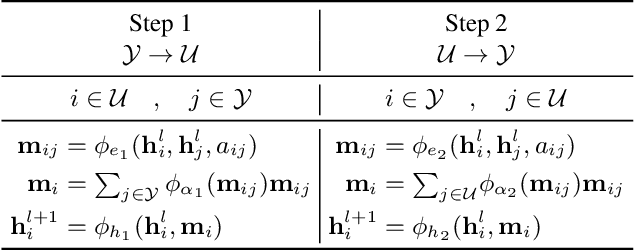
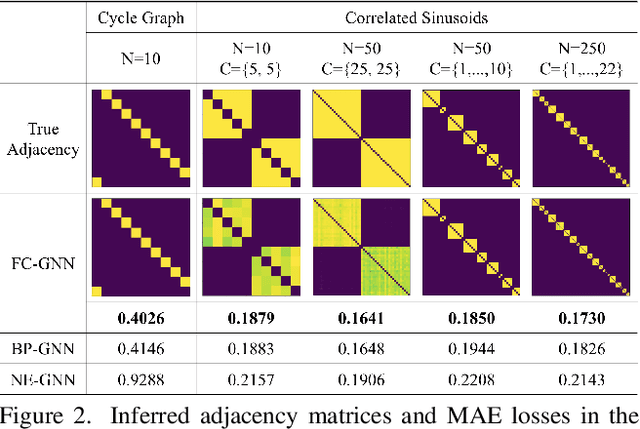
This paper introduces a new approach for Multivariate Time Series forecasting that jointly infers and leverages relations among time series. Its modularity allows it to be integrated with current univariate methods. Our approach allows to trade-off accuracy and computational efficiency gradually via offering on one extreme inference of a potentially fully-connected graph or on another extreme a bipartite graph. In the potentially fully-connected case we consider all pair-wise interactions among time-series which yields the best forecasting accuracy. Conversely, the bipartite case leverages the dependency structure by inter-communicating the N time series through a small set of K auxiliary nodes that we introduce. This reduces the time and memory complexity w.r.t. previous graph inference methods from O(N^2) to O(NK) with a small trade-off in accuracy. We demonstrate the effectiveness of our model in a variety of datasets where both of its variants perform better or very competitively to previous graph inference methods in terms of forecasting accuracy and time efficiency.

Neural Flows: Efficient Alternative to Neural ODEs

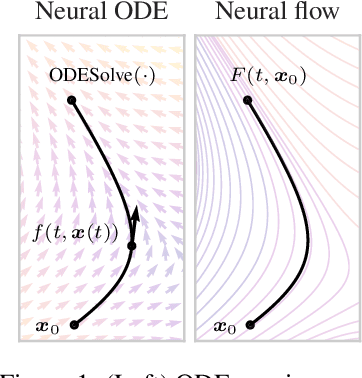
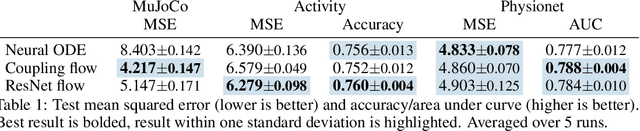
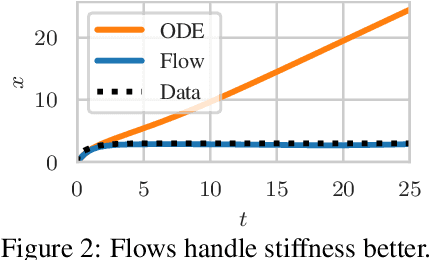
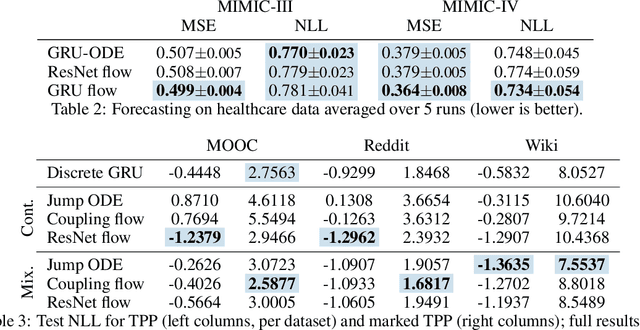
Neural ordinary differential equations describe how values change in time. This is the reason why they gained importance in modeling sequential data, especially when the observations are made at irregular intervals. In this paper we propose an alternative by directly modeling the solution curves - the flow of an ODE - with a neural network. This immediately eliminates the need for expensive numerical solvers while still maintaining the modeling capability of neural ODEs. We propose several flow architectures suitable for different applications by establishing precise conditions on when a function defines a valid flow. Apart from computational efficiency, we also provide empirical evidence of favorable generalization performance via applications in time series modeling, forecasting, and density estimation.

Neural forecasting: Introduction and literature overview

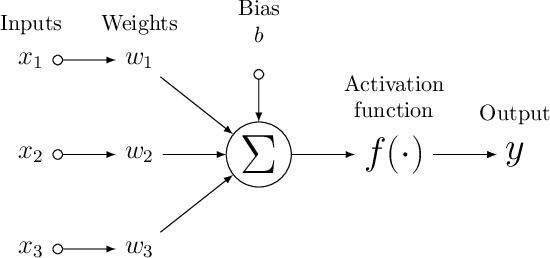
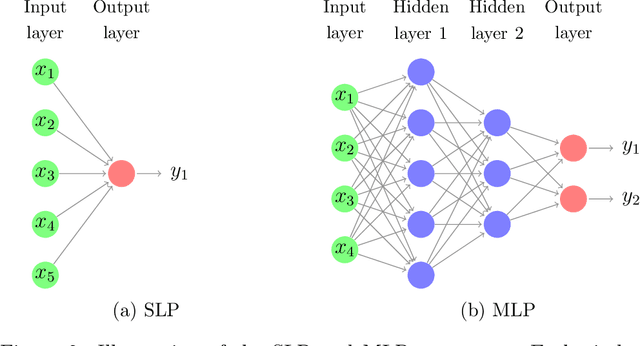
Neural network based forecasting methods have become ubiquitous in large-scale industrial forecasting applications over the last years. As the prevalence of neural network based solutions among the best entries in the recent M4 competition shows, the recent popularity of neural forecasting methods is not limited to industry and has also reached academia. This article aims at providing an introduction and an overview of some of the advances that have permitted the resurgence of neural networks in machine learning. Building on these foundations, the article then gives an overview of the recent literature on neural networks for forecasting and applications.

Methods for Sparse and Low-Rank Recovery under Simplex Constraints

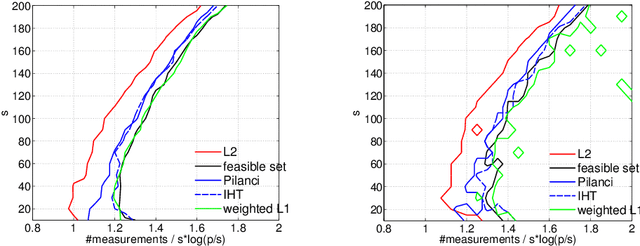
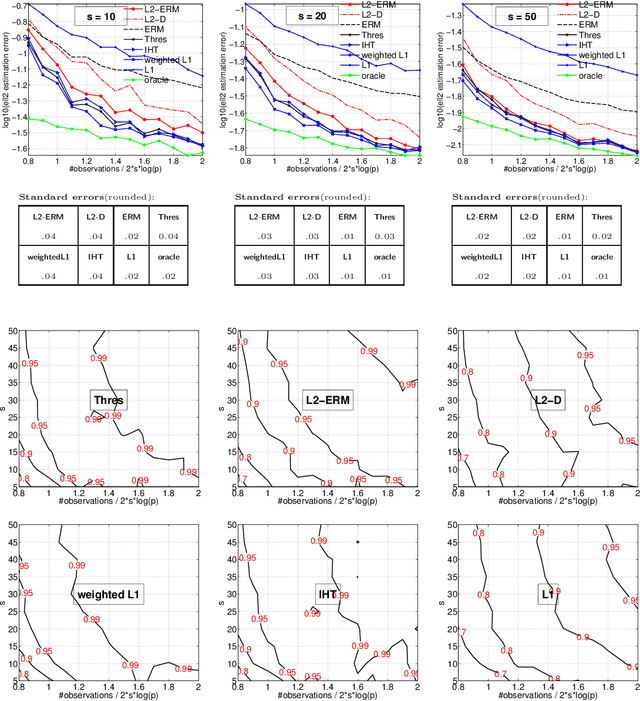
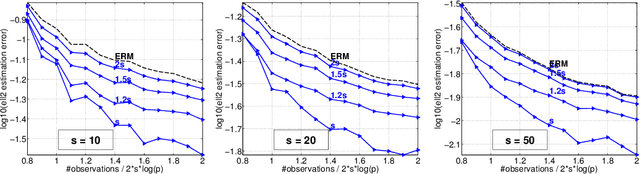
The de-facto standard approach of promoting sparsity by means of $\ell_1$-regularization becomes ineffective in the presence of simplex constraints, i.e.,~the target is known to have non-negative entries summing up to a given constant. The situation is analogous for the use of nuclear norm regularization for low-rank recovery of Hermitian positive semidefinite matrices with given trace. In the present paper, we discuss several strategies to deal with this situation, from simple to more complex. As a starting point, we consider empirical risk minimization (ERM). It follows from existing theory that ERM enjoys better theoretical properties w.r.t.~prediction and $\ell_2$-estimation error than $\ell_1$-regularization. In light of this, we argue that ERM combined with a subsequent sparsification step like thresholding is superior to the heuristic of using $\ell_1$-regularization after dropping the sum constraint and subsequent normalization. At the next level, we show that any sparsity-promoting regularizer under simplex constraints cannot be convex. A novel sparsity-promoting regularization scheme based on the inverse or negative of the squared $\ell_2$-norm is proposed, which avoids shortcomings of various alternative methods from the literature. Our approach naturally extends to Hermitian positive semidefinite matrices with given trace. Numerical studies concerning compressed sensing, sparse mixture density estimation, portfolio optimization and quantum state tomography are used to illustrate the key points of the paper.

Constrained 1-Spectral Clustering

An important form of prior information in clustering comes in form of cannot-link and must-link constraints. We present a generalization of the popular spectral clustering technique which integrates such constraints. Motivated by the recently proposed $1$-spectral clustering for the unconstrained problem, our method is based on a tight relaxation of the constrained normalized cut into a continuous optimization problem. Opposite to all other methods which have been suggested for constrained spectral clustering, we can always guarantee to satisfy all constraints. Moreover, our soft formulation allows to optimize a trade-off between normalized cut and the number of violated constraints. An efficient implementation is provided which scales to large datasets. We outperform consistently all other proposed methods in the experiments.

Tight Continuous Relaxation of the Balanced $k$-Cut Problem

Spectral Clustering as a relaxation of the normalized/ratio cut has become one of the standard graph-based clustering methods. Existing methods for the computation of multiple clusters, corresponding to a balanced $k$-cut of the graph, are either based on greedy techniques or heuristics which have weak connection to the original motivation of minimizing the normalized cut. In this paper we propose a new tight continuous relaxation for any balanced $k$-cut problem and show that a related recently proposed relaxation is in most cases loose leading to poor performance in practice. For the optimization of our tight continuous relaxation we propose a new algorithm for the difficult sum-of-ratios minimization problem which achieves monotonic descent. Extensive comparisons show that our method outperforms all existing approaches for ratio cut and other balanced $k$-cut criteria.

The Total Variation on Hypergraphs - Learning on Hypergraphs Revisited

Hypergraphs allow one to encode higher-order relationships in data and are thus a very flexible modeling tool. Current learning methods are either based on approximations of the hypergraphs via graphs or on tensor methods which are only applicable under special conditions. In this paper, we present a new learning framework on hypergraphs which fully uses the hypergraph structure. The key element is a family of regularization functionals based on the total variation on hypergraphs.