Constrained 1-Spectral Clustering
Paper and Code
May 24, 2015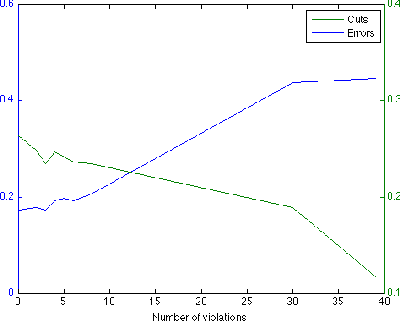
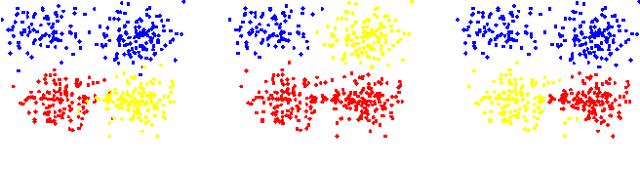

An important form of prior information in clustering comes in form of cannot-link and must-link constraints. We present a generalization of the popular spectral clustering technique which integrates such constraints. Motivated by the recently proposed $1$-spectral clustering for the unconstrained problem, our method is based on a tight relaxation of the constrained normalized cut into a continuous optimization problem. Opposite to all other methods which have been suggested for constrained spectral clustering, we can always guarantee to satisfy all constraints. Moreover, our soft formulation allows to optimize a trade-off between normalized cut and the number of violated constraints. An efficient implementation is provided which scales to large datasets. We outperform consistently all other proposed methods in the experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge