Methods for Sparse and Low-Rank Recovery under Simplex Constraints

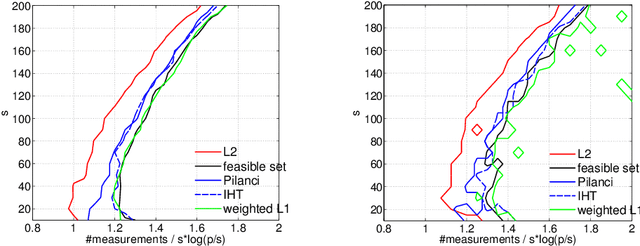
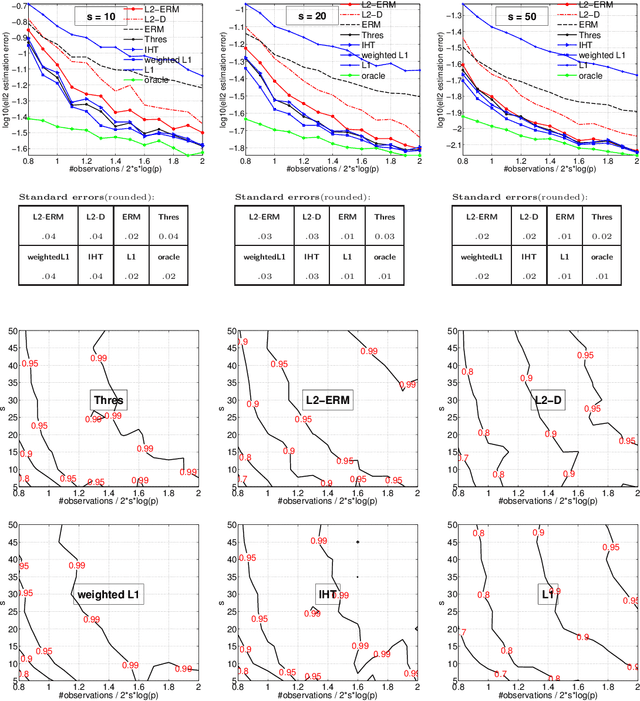
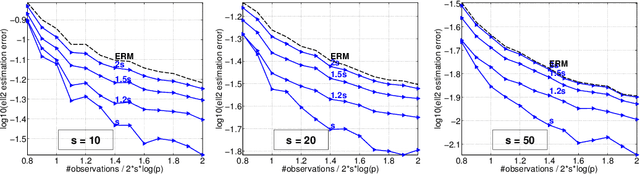
The de-facto standard approach of promoting sparsity by means of $\ell_1$-regularization becomes ineffective in the presence of simplex constraints, i.e.,~the target is known to have non-negative entries summing up to a given constant. The situation is analogous for the use of nuclear norm regularization for low-rank recovery of Hermitian positive semidefinite matrices with given trace. In the present paper, we discuss several strategies to deal with this situation, from simple to more complex. As a starting point, we consider empirical risk minimization (ERM). It follows from existing theory that ERM enjoys better theoretical properties w.r.t.~prediction and $\ell_2$-estimation error than $\ell_1$-regularization. In light of this, we argue that ERM combined with a subsequent sparsification step like thresholding is superior to the heuristic of using $\ell_1$-regularization after dropping the sum constraint and subsequent normalization. At the next level, we show that any sparsity-promoting regularizer under simplex constraints cannot be convex. A novel sparsity-promoting regularization scheme based on the inverse or negative of the squared $\ell_2$-norm is proposed, which avoids shortcomings of various alternative methods from the literature. Our approach naturally extends to Hermitian positive semidefinite matrices with given trace. Numerical studies concerning compressed sensing, sparse mixture density estimation, portfolio optimization and quantum state tomography are used to illustrate the key points of the paper.