Martin Slawski
Lasso Penalization for High-Dimensional Beta Regression Models: Computation, Analysis, and Inference
Jul 26, 2025
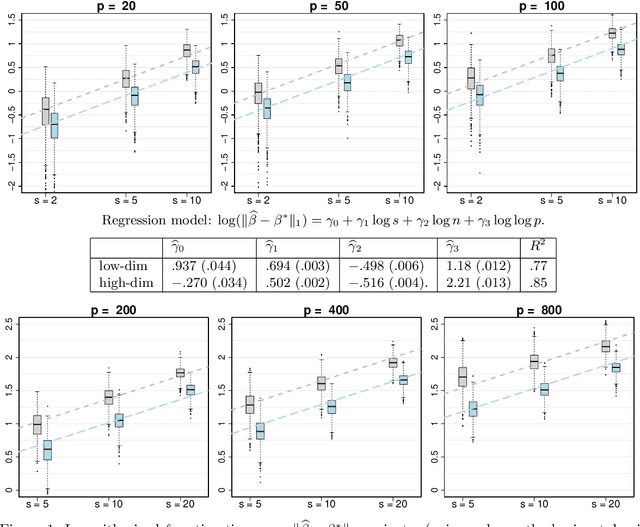
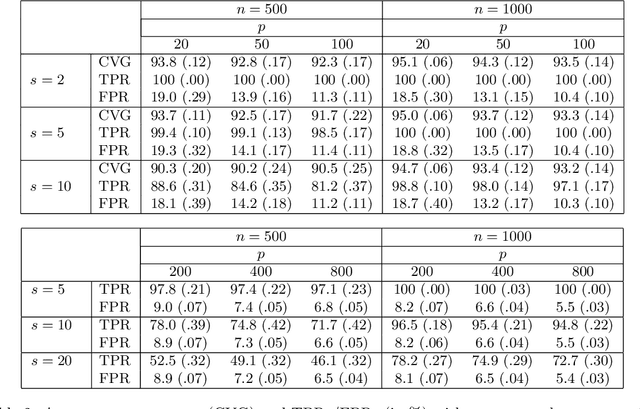
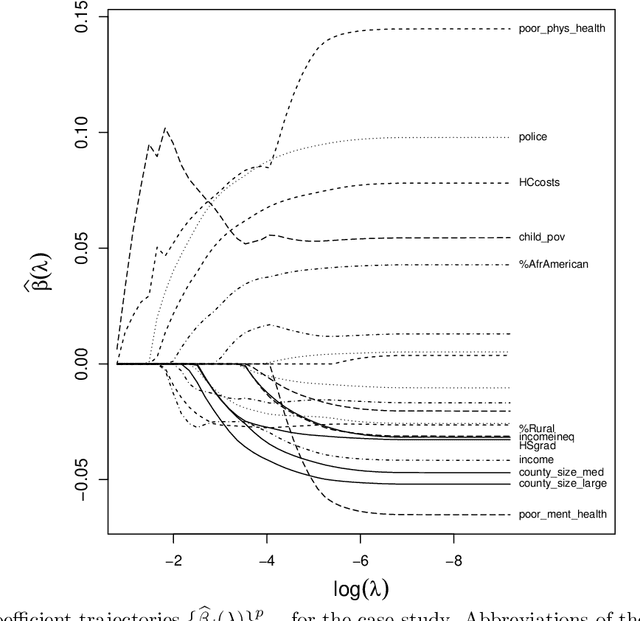
Abstract:Beta regression is commonly employed when the outcome variable is a proportion. Since its conception, the approach has been widely used in applications spanning various scientific fields. A series of extensions have been proposed over time, several of which address variable selection and penalized estimation, e.g., with an $\ell_1$-penalty (LASSO). However, a theoretical analysis of this popular approach in the context of Beta regression with high-dimensional predictors is lacking. In this paper, we aim to close this gap. A particular challenge arises from the non-convexity of the associated negative log-likelihood, which we address by resorting to a framework for analyzing stationary points in a neighborhood of the target parameter. Leveraging this framework, we derive a non-asymptotic bound on the $\ell_1$-error of such stationary points. In addition, we propose a debiasing approach to construct confidence intervals for the regression parameters. A proximal gradient algorithm is devised for optimizing the resulting penalized negative log-likelihood function. Our theoretical analysis is corroborated via simulation studies, and a real data example concerning the prediction of county-level proportions of incarceration is presented to showcase the practical utility of our methodology.
Permuted and Unlinked Monotone Regression in $\mathbb{R}^d$: an approach based on mixture modeling and optimal transport
Jan 10, 2022

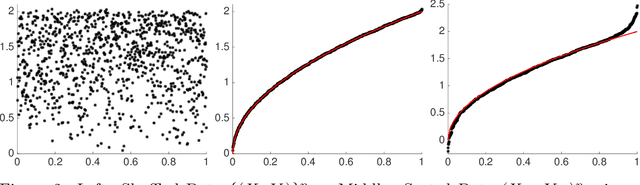
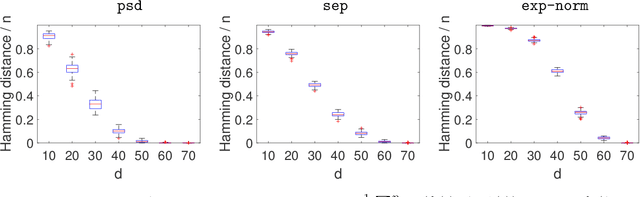
Abstract:Suppose that we have a regression problem with response variable Y in $\mathbb{R}^d$ and predictor X in $\mathbb{R}^d$, for $d \geq 1$. In permuted or unlinked regression we have access to separate unordered data on X and Y, as opposed to data on (X,Y)-pairs in usual regression. So far in the literature the case $d=1$ has received attention, see e.g., the recent papers by Rigollet and Weed [Information & Inference, 8, 619--717] and Balabdaoui et al. [J. Mach. Learn. Res., 22(172), 1--60]. In this paper, we consider the general multivariate setting with $d \geq 1$. We show that the notion of cyclical monotonicity of the regression function is sufficient for identification and estimation in the permuted/unlinked regression model. We study permutation recovery in the permuted regression setting and develop a computationally efficient and easy-to-use algorithm for denoising based on the Kiefer-Wolfowitz [Ann. Math. Statist., 27, 887--906] nonparametric maximum likelihood estimator and techniques from the theory of optimal transport. We provide explicit upper bounds on the associated mean squared denoising error for Gaussian noise. As in previous work on the case $d = 1$, the permuted/unlinked setting involves slow (logarithmic) rates of convergence rooting in the underlying deconvolution problem. Numerical studies corroborate our theoretical analysis and show that the proposed approach performs at least on par with the methods in the aforementioned prior work in the case $d = 1$ while achieving substantial reductions in terms of computational complexity.
Regularization for Shuffled Data Problems via Exponential Family Priors on the Permutation Group
Nov 02, 2021



Abstract:In the analysis of data sets consisting of (X, Y)-pairs, a tacit assumption is that each pair corresponds to the same observation unit. If, however, such pairs are obtained via record linkage of two files, this assumption can be violated as a result of mismatch error rooting, for example, in the lack of reliable identifiers in the two files. Recently, there has been a surge of interest in this setting under the term "Shuffled data" in which the underlying correct pairing of (X, Y)-pairs is represented via an unknown index permutation. Explicit modeling of the permutation tends to be associated with substantial overfitting, prompting the need for suitable methods of regularization. In this paper, we propose a flexible exponential family prior on the permutation group for this purpose that can be used to integrate various structures such as sparse and locally constrained shuffling. This prior turns out to be conjugate for canonical shuffled data problems in which the likelihood conditional on a fixed permutation can be expressed as product over the corresponding (X,Y)-pairs. Inference is based on the EM algorithm in which the intractable E-step is approximated by the Fisher-Yates algorithm. The M-step is shown to admit a significant reduction from $n^2$ to $n$ terms if the likelihood of (X,Y)-pairs has exponential family form as in the case of generalized linear models. Comparisons on synthetic and real data show that the proposed approach compares favorably to competing methods.
A Pseudo-Likelihood Approach to Linear Regression with Partially Shuffled Data
Oct 03, 2019

Abstract:Recently, there has been significant interest in linear regression in the situation where predictors and responses are not observed in matching pairs corresponding to the same statistical unit as a consequence of separate data collection and uncertainty in data integration. Mismatched pairs can considerably impact the model fit and disrupt the estimation of regression parameters. In this paper, we present a method to adjust for such mismatches under ``partial shuffling" in which a sufficiently large fraction of (predictors, response)-pairs are observed in their correct correspondence. The proposed approach is based on a pseudo-likelihood in which each term takes the form of a two-component mixture density. Expectation-Maximization schemes are proposed for optimization, which (i) scale favorably in the number of samples, and (ii) achieve excellent statistical performance relative to an oracle that has access to the correct pairings as certified by simulations and case studies. In particular, the proposed approach can tolerate considerably larger fraction of mismatches than existing approaches, and enables estimation of the noise level as well as the fraction of mismatches. Inference for the resulting estimator (standard errors, confidence intervals) can be based on established theory for composite likelihood estimation. Along the way, we also propose a statistical test for the presence of mismatches and establish its consistency under suitable conditions.
Permutation Recovery from Multiple Measurement Vectors in Unlabeled Sensing
Sep 05, 2019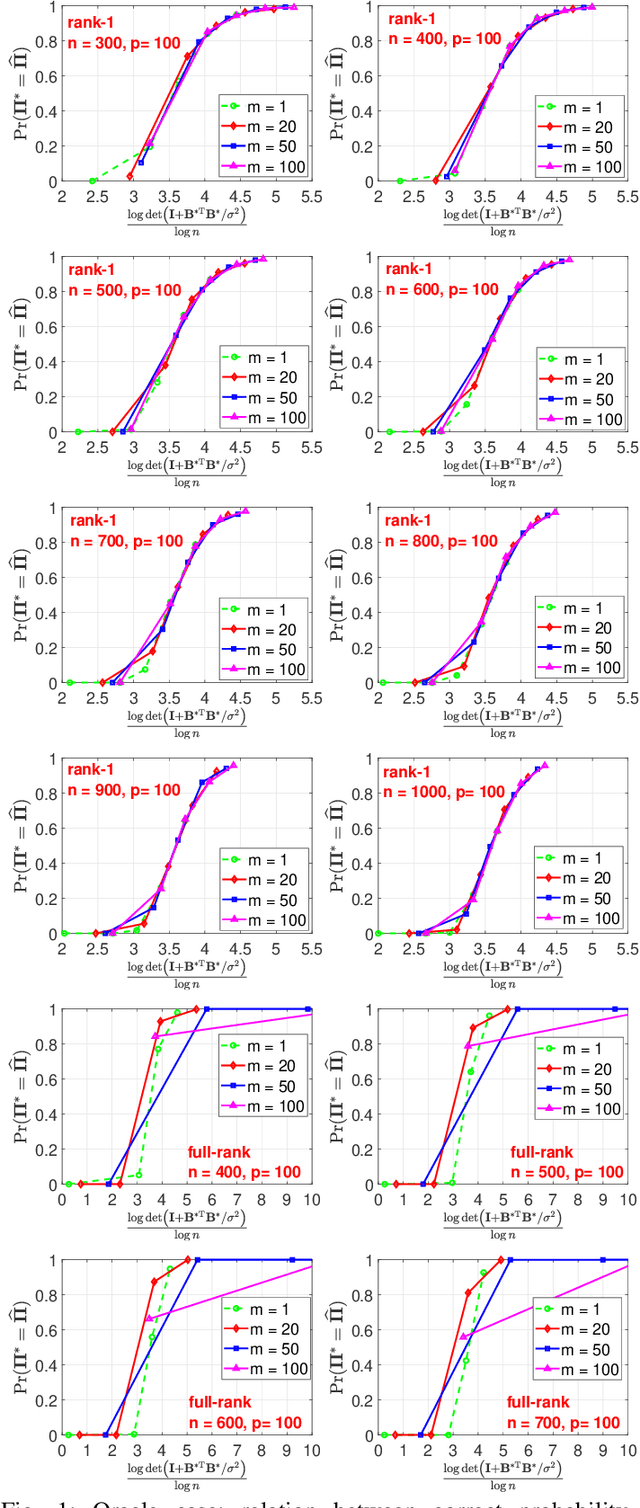
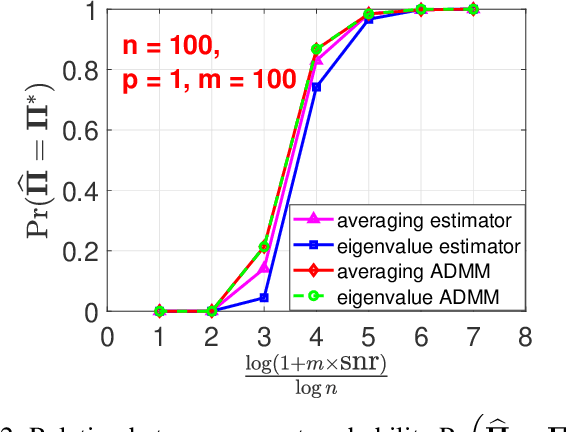
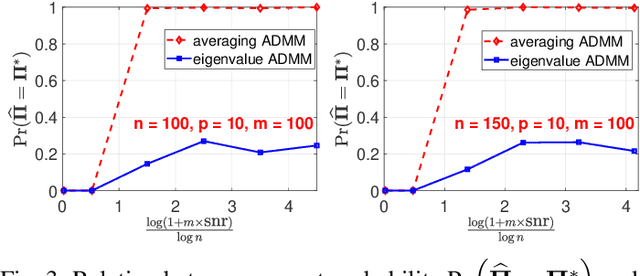
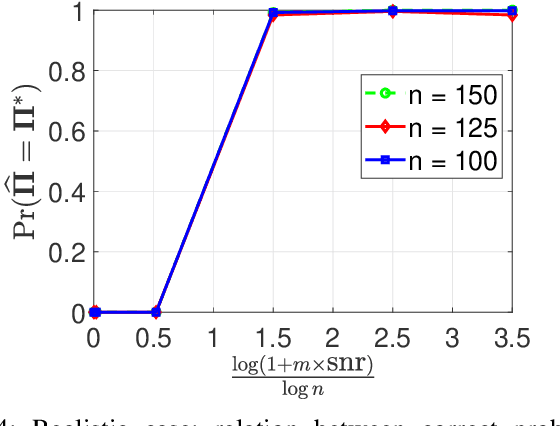
Abstract:In "Unlabeled Sensing", one observes a set of linear measurements of an underlying signal with incomplete or missing information about their ordering, which can be modeled in terms of an unknown permutation. Previous work on the case of a single noisy measurement vector has exposed two main challenges: 1) a high requirement concerning the \emph{signal-to-noise ratio} (snr), i.e., approximately of the order of $n^{5}$, and 2) a massive computational burden in light of NP-hardness in general. In this paper, we study the case of \emph{multiple} noisy measurement vectors (MMVs) resulting from a \emph{common} permutation and investigate to what extent the number of MMVs $m$ facilitates permutation recovery by "borrowing strength". The above two challenges have at least partially been resolved within our work. First, we show that a large stable rank of the signal significantly reduces the required snr which can drop from a polynomial in $n$ for $m = 1$ to a constant for $m = \Omega(\log n)$, where $m$ denotes the number of MMVs and $n$ denotes the number of measurements per MV. This bound is shown to be sharp and is associated with a phase transition phenomenon. Second, we propose computational schemes for recovering the unknown permutation in practice. For the "oracle case" with the known signal, the maximum likelihood (ML) estimator reduces to a linear assignment problem whose global optimum can be obtained efficiently. For the case in which both the signal and permutation are unknown, the problem is reformulated as a bi-convex optimization problem with an auxiliary variable, which can be solved by the Alternating Direction Method of Multipliers (ADMM). Numerical experiments based on the proposed computational schemes confirm the tightness of our theoretical analysis.
A Two-Stage Approach to Multivariate Linear Regression with Sparsely Mismatched Data
Jul 16, 2019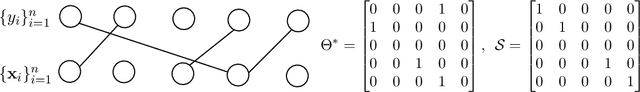
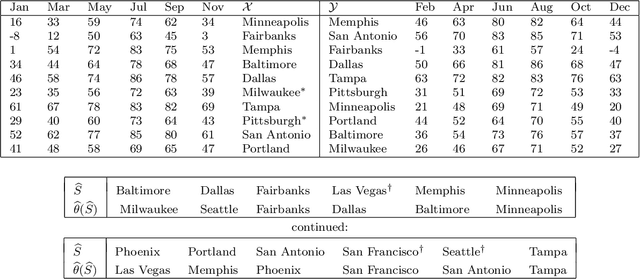
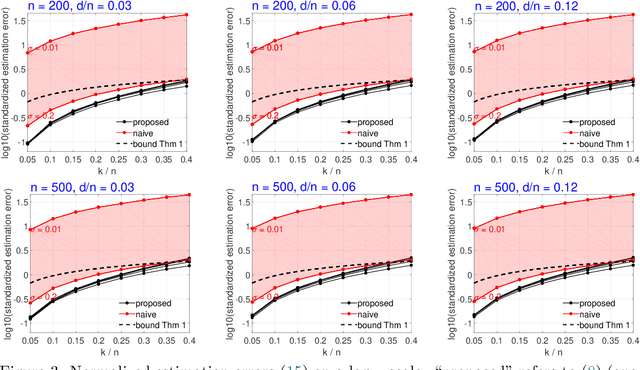
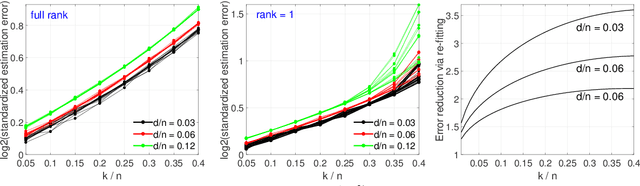
Abstract:A tacit assumption in linear regression is that (response, predictor)-pairs correspond to identical observational units. A series of recent works have studied scenarios in which this assumption is violated under terms such as ``Unlabeled Sensing and ``Regression with Unknown Permutation''. In this paper, we study the setup of multiple response variables and a notion of mismatches that generalizes permutations in order to allow for missing matches as well as for one-to-many matches. A two-stage method is proposed under the assumption that most pairs are correctly matched. In the first stage, the regression parameter is estimated by handling mismatches as contaminations, and subsequently the generalized permutation is estimated by a basic variant of matching. The approach is both computationally convenient and equipped with favorable statistical guarantees. Specifically, it is shown that the conditions for permutation recovery become considerably less stringent as the number of responses $m$ per observation increase. Particularly, for $m = \Omega(\log n)$, the required signal-to-noise ratio does no longer depend on the sample size $n$. Numerical results on synthetic and real data are presented to support the main findings of our analysis.
A Note on Coding and Standardization of Categorical Variables in Group Lasso Regression
May 17, 2018

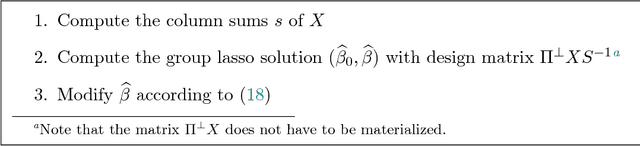

Abstract:Categorical regressor variables are usually handled by introducing a set of indicator variables, and imposing a linear constraint to ensure identifiability in the presence of an intercept, or equivalently, using one of various coding schemes. As proposed in Yuan and Lin [J. R. Statist. Soc. B, 68 (2006), 49-67], the group lasso is a natural and computationally convenient approach to perform variable selection in settings with categorical covariates. As pointed out by Simon and Tibshirani [Stat. Sin., 22 (2011), 983-1001], "standardization" by means of block-wise orthonormalization of column submatrices each corresponding to one group of variables can substantially boost performance. In this note, we study the aspect of standardization for the special case of categorical predictors in detail. The main result is that orthonormalization is not required; column-wise scaling of the design matrix followed by re-scaling and centering of the coefficients is shown to have exactly the same effect. Similar reductions can be achieved in the case of interactions. The extension to the so-called sparse group lasso, which additionally promotes within-group sparsity, is considered as well. The importance of proper standardization is illustrated via extensive simulations.
Linear Regression with Sparsely Permuted Data
Nov 15, 2017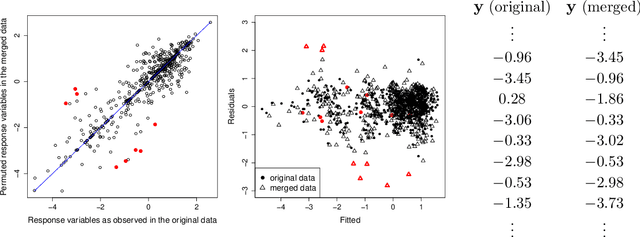


Abstract:In regression analysis of multivariate data, it is tacitly assumed that response and predictor variables in each observed response-predictor pair correspond to the same entity or unit. In this paper, we consider the situation of "permuted data" in which this basic correspondence has been lost. Several recent papers have considered this situation without further assumptions on the underlying permutation. In applications, the latter is often to known to have additional structure that can be leveraged. Specifically, we herein consider the common scenario of "sparsely permuted data" in which only a small fraction of the data is affected by a mismatch between response and predictors. However, an adverse effect already observed for sparsely permuted data is that the least squares estimator as well as other estimators not accounting for such partial mismatch are inconsistent. One approach studied in detail herein is to treat permuted data as outliers which motivates the use of robust regression formulations to estimate the regression parameter. The resulting estimate can subsequently be used to recover the permutation. A notable benefit of the proposed approach is its computational simplicity given the general lack of procedures for the above problem that are both statistically sound and computationally appealing.
On Principal Components Regression, Random Projections, and Column Subsampling
Oct 08, 2017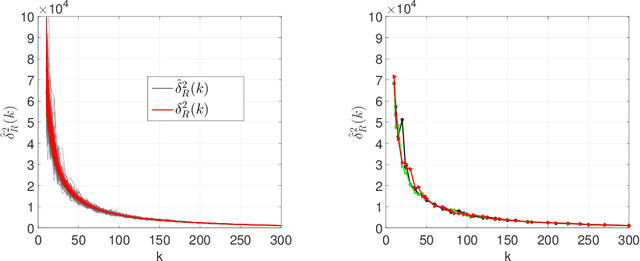

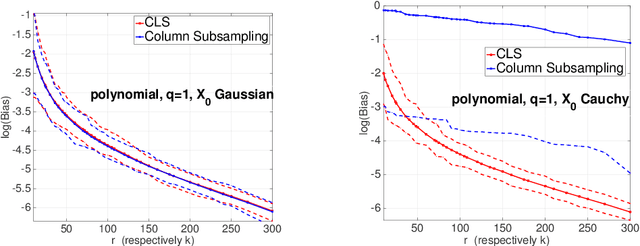
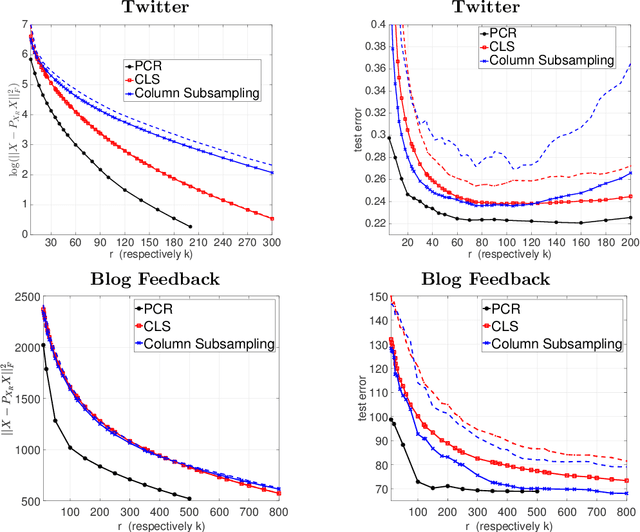
Abstract:Principal Components Regression (PCR) is a traditional tool for dimension reduction in linear regression that has been both criticized and defended. One concern about PCR is that obtaining the leading principal components tends to be computationally demanding for large data sets. While random projections do not possess the optimality properties of the leading principal subspace, they are computationally appealing and hence have become increasingly popular in recent years. In this paper, we present an analysis showing that for random projections satisfying a Johnson-Lindenstrauss embedding property, the prediction error in subsequent regression is close to that of PCR, at the expense of requiring a slightly large number of random projections than principal components. Column sub-sampling constitutes an even cheaper way of randomized dimension reduction outside the class of Johnson-Lindenstrauss transforms. We provide numerical results based on synthetic and real data as well as basic theory revealing differences and commonalities in terms of statistical performance.
Methods for Sparse and Low-Rank Recovery under Simplex Constraints
May 02, 2016
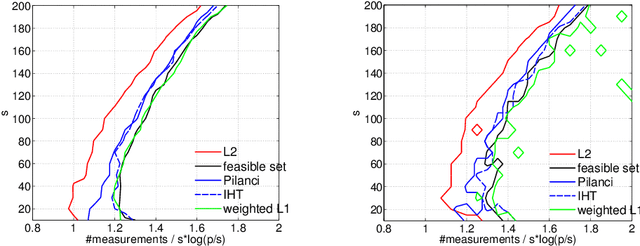
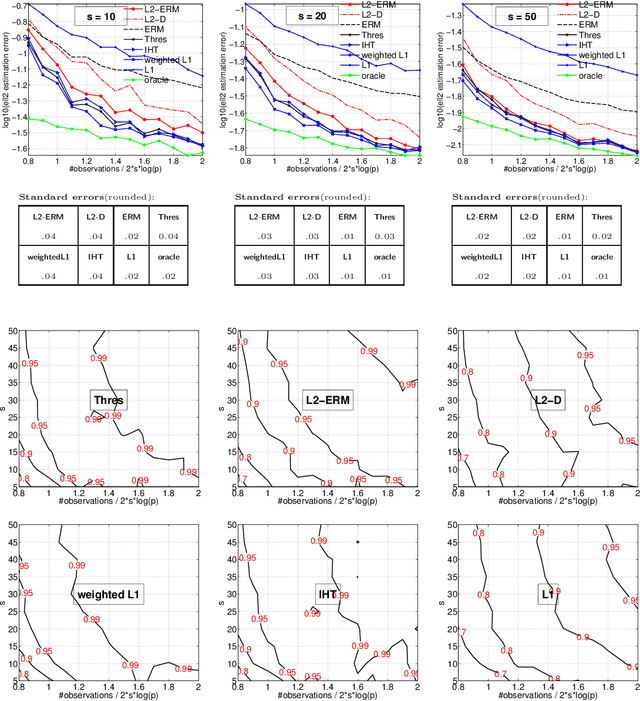
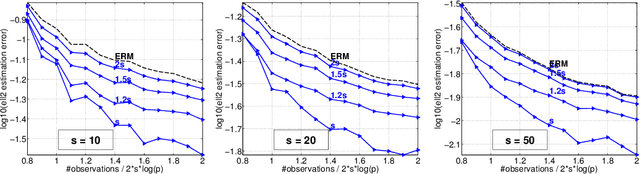
Abstract:The de-facto standard approach of promoting sparsity by means of $\ell_1$-regularization becomes ineffective in the presence of simplex constraints, i.e.,~the target is known to have non-negative entries summing up to a given constant. The situation is analogous for the use of nuclear norm regularization for low-rank recovery of Hermitian positive semidefinite matrices with given trace. In the present paper, we discuss several strategies to deal with this situation, from simple to more complex. As a starting point, we consider empirical risk minimization (ERM). It follows from existing theory that ERM enjoys better theoretical properties w.r.t.~prediction and $\ell_2$-estimation error than $\ell_1$-regularization. In light of this, we argue that ERM combined with a subsequent sparsification step like thresholding is superior to the heuristic of using $\ell_1$-regularization after dropping the sum constraint and subsequent normalization. At the next level, we show that any sparsity-promoting regularizer under simplex constraints cannot be convex. A novel sparsity-promoting regularization scheme based on the inverse or negative of the squared $\ell_2$-norm is proposed, which avoids shortcomings of various alternative methods from the literature. Our approach naturally extends to Hermitian positive semidefinite matrices with given trace. Numerical studies concerning compressed sensing, sparse mixture density estimation, portfolio optimization and quantum state tomography are used to illustrate the key points of the paper.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge