A Pseudo-Likelihood Approach to Linear Regression with Partially Shuffled Data
Paper and Code
Oct 03, 2019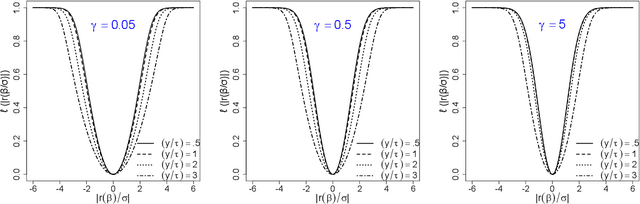
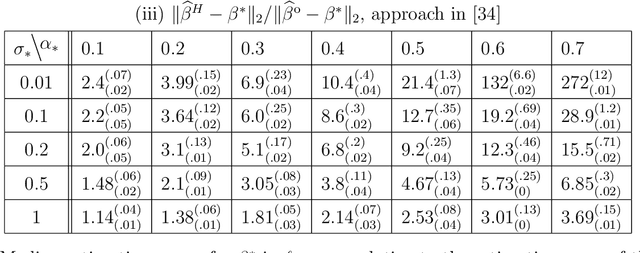
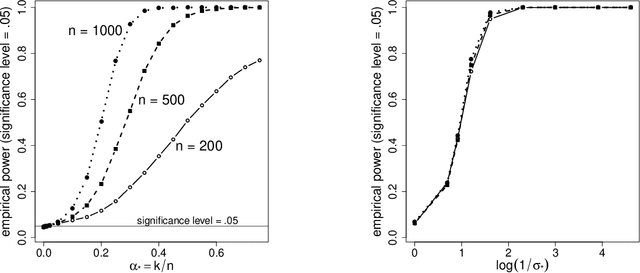

Recently, there has been significant interest in linear regression in the situation where predictors and responses are not observed in matching pairs corresponding to the same statistical unit as a consequence of separate data collection and uncertainty in data integration. Mismatched pairs can considerably impact the model fit and disrupt the estimation of regression parameters. In this paper, we present a method to adjust for such mismatches under ``partial shuffling" in which a sufficiently large fraction of (predictors, response)-pairs are observed in their correct correspondence. The proposed approach is based on a pseudo-likelihood in which each term takes the form of a two-component mixture density. Expectation-Maximization schemes are proposed for optimization, which (i) scale favorably in the number of samples, and (ii) achieve excellent statistical performance relative to an oracle that has access to the correct pairings as certified by simulations and case studies. In particular, the proposed approach can tolerate considerably larger fraction of mismatches than existing approaches, and enables estimation of the noise level as well as the fraction of mismatches. Inference for the resulting estimator (standard errors, confidence intervals) can be based on established theory for composite likelihood estimation. Along the way, we also propose a statistical test for the presence of mismatches and establish its consistency under suitable conditions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge