A Unified Causal Inference Framework for the Desirability of Outcome Ranking Paradigm in Benefit-Risk Evaluation

We developed a unified covariate-adjusted causal inference framework for estimating the desirability of outcome ranking (DOOR) probability for benefit-risk evaluation in randomized trials and observational studies. The framework expresses the DOOR probability as a bilinear functional of the marginal ordinal outcome distributions under the two treatment strategies, estimates conditional ordinal distributions through sequential risk-set hazards, and derives the efficient influence function (EIF) of the DOOR probability. The point-estimation simulations compared G-computation, normalized inverse probability weighting (IPW), augmented IPW (AIPW), and targeted maximum likelihood estimation (TMLE), with nuisance functions estimated using generalized linear models or Super Learner (SL). TMLE-SL showed the strongest and most consistent point-estimation performance, with AIPW-SL ranking second. EIF-based inference was then evaluated for AIPW-SL and TMLE-SL, with and without cross-fitting, across settings varying in overlap, treatment-effect heterogeneity, and treatment allocation. CVTMLE-SL showed the strongest overall performance across DOOR-scale bias, recovery of the underlying ordinal distributions, standard-error accuracy, and confidence-interval coverage. We illustrate the methodology using data from the multidrug-resistant organism network of the Antibacterial Resistance Leadership Group.

A Pseudo-Likelihood Approach to Linear Regression with Partially Shuffled Data

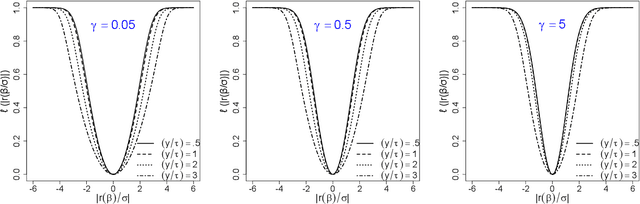
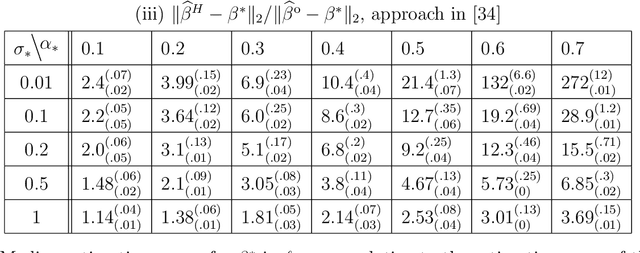
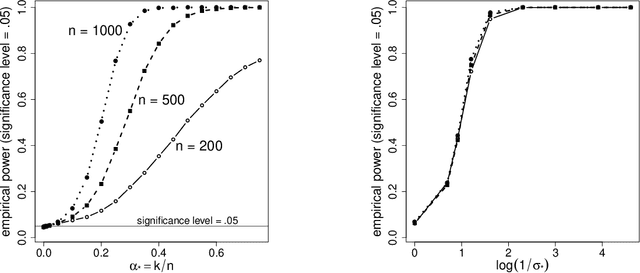
Recently, there has been significant interest in linear regression in the situation where predictors and responses are not observed in matching pairs corresponding to the same statistical unit as a consequence of separate data collection and uncertainty in data integration. Mismatched pairs can considerably impact the model fit and disrupt the estimation of regression parameters. In this paper, we present a method to adjust for such mismatches under ``partial shuffling" in which a sufficiently large fraction of (predictors, response)-pairs are observed in their correct correspondence. The proposed approach is based on a pseudo-likelihood in which each term takes the form of a two-component mixture density. Expectation-Maximization schemes are proposed for optimization, which (i) scale favorably in the number of samples, and (ii) achieve excellent statistical performance relative to an oracle that has access to the correct pairings as certified by simulations and case studies. In particular, the proposed approach can tolerate considerably larger fraction of mismatches than existing approaches, and enables estimation of the noise level as well as the fraction of mismatches. Inference for the resulting estimator (standard errors, confidence intervals) can be based on established theory for composite likelihood estimation. Along the way, we also propose a statistical test for the presence of mismatches and establish its consistency under suitable conditions.