Regularization for Shuffled Data Problems via Exponential Family Priors on the Permutation Group

In the analysis of data sets consisting of (X, Y)-pairs, a tacit assumption is that each pair corresponds to the same observation unit. If, however, such pairs are obtained via record linkage of two files, this assumption can be violated as a result of mismatch error rooting, for example, in the lack of reliable identifiers in the two files. Recently, there has been a surge of interest in this setting under the term "Shuffled data" in which the underlying correct pairing of (X, Y)-pairs is represented via an unknown index permutation. Explicit modeling of the permutation tends to be associated with substantial overfitting, prompting the need for suitable methods of regularization. In this paper, we propose a flexible exponential family prior on the permutation group for this purpose that can be used to integrate various structures such as sparse and locally constrained shuffling. This prior turns out to be conjugate for canonical shuffled data problems in which the likelihood conditional on a fixed permutation can be expressed as product over the corresponding (X,Y)-pairs. Inference is based on the EM algorithm in which the intractable E-step is approximated by the Fisher-Yates algorithm. The M-step is shown to admit a significant reduction from $n^2$ to $n$ terms if the likelihood of (X,Y)-pairs has exponential family form as in the case of generalized linear models. Comparisons on synthetic and real data show that the proposed approach compares favorably to competing methods.

Predicting Census Survey Response Rates via Interpretable Nonparametric Additive Models with Structured Interactions

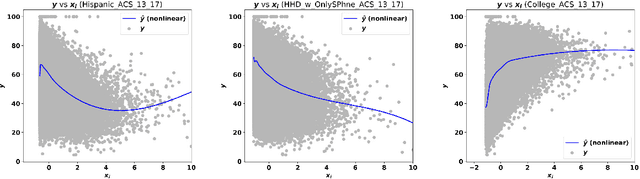
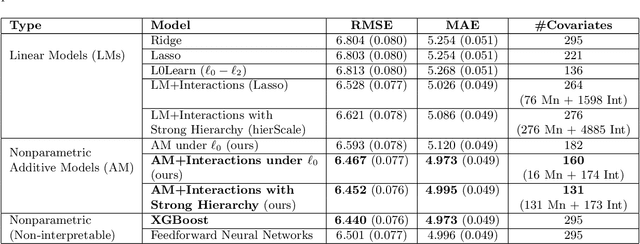
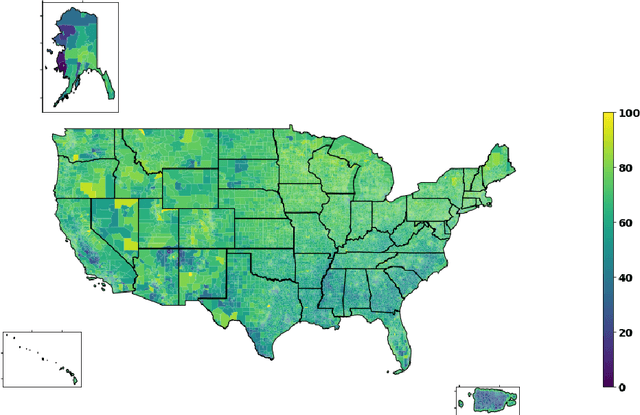
Accurate and interpretable prediction of survey response rates is important from an operational standpoint. The US Census Bureau's well-known ROAM application uses principled statistical models trained on the US Census Planning Database data to identify hard-to-survey areas. An earlier crowdsourcing competition revealed that an ensemble of regression trees led to the best performance in predicting survey response rates; however, the corresponding models could not be adopted for the intended application due to limited interpretability. In this paper, we present new interpretable statistical methods to predict, with high accuracy, response rates in surveys. We study sparse nonparametric additive models with pairwise interactions via $\ell_0$-regularization, as well as hierarchically structured variants that provide enhanced interpretability. Despite strong methodological underpinnings, such models can be computationally challenging -- we present new scalable algorithms for learning these models. We also establish novel non-asymptotic error bounds for the proposed estimators. Experiments based on the US Census Planning Database demonstrate that our methods lead to high-quality predictive models that permit actionable interpretability for different segments of the population. Interestingly, our methods provide significant gains in interpretability without losing in predictive performance to state-of-the-art black-box machine learning methods based on gradient boosting and feedforward neural networks. Our code implementation in python is available at https://github.com/ShibalIbrahim/Additive-Models-with-Structured-Interactions.

A Pseudo-Likelihood Approach to Linear Regression with Partially Shuffled Data

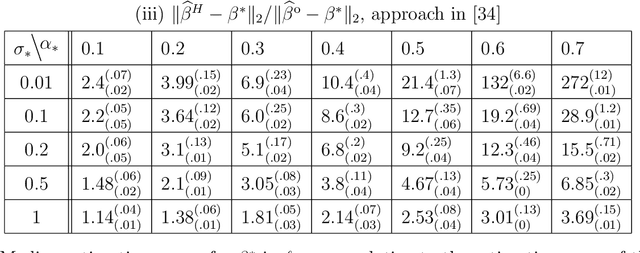
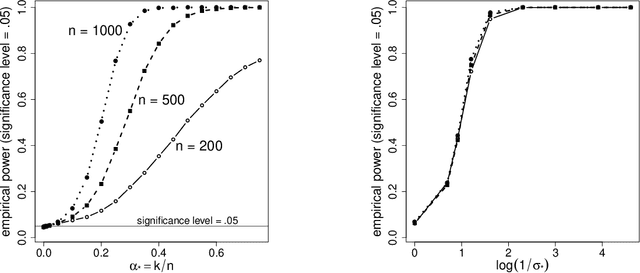
Recently, there has been significant interest in linear regression in the situation where predictors and responses are not observed in matching pairs corresponding to the same statistical unit as a consequence of separate data collection and uncertainty in data integration. Mismatched pairs can considerably impact the model fit and disrupt the estimation of regression parameters. In this paper, we present a method to adjust for such mismatches under ``partial shuffling" in which a sufficiently large fraction of (predictors, response)-pairs are observed in their correct correspondence. The proposed approach is based on a pseudo-likelihood in which each term takes the form of a two-component mixture density. Expectation-Maximization schemes are proposed for optimization, which (i) scale favorably in the number of samples, and (ii) achieve excellent statistical performance relative to an oracle that has access to the correct pairings as certified by simulations and case studies. In particular, the proposed approach can tolerate considerably larger fraction of mismatches than existing approaches, and enables estimation of the noise level as well as the fraction of mismatches. Inference for the resulting estimator (standard errors, confidence intervals) can be based on established theory for composite likelihood estimation. Along the way, we also propose a statistical test for the presence of mismatches and establish its consistency under suitable conditions.

A Two-Stage Approach to Multivariate Linear Regression with Sparsely Mismatched Data

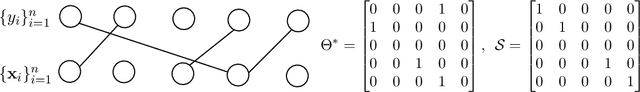
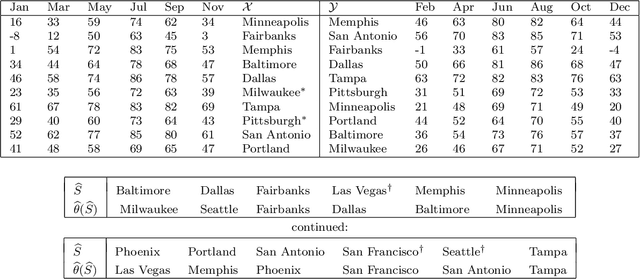
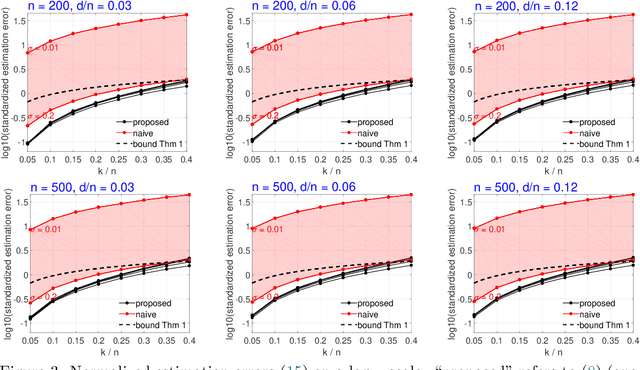
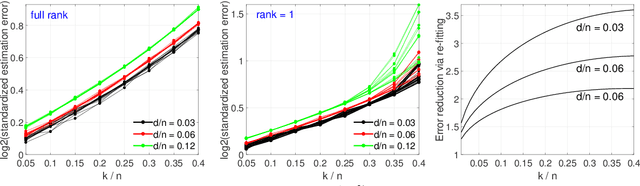
A tacit assumption in linear regression is that (response, predictor)-pairs correspond to identical observational units. A series of recent works have studied scenarios in which this assumption is violated under terms such as ``Unlabeled Sensing and ``Regression with Unknown Permutation''. In this paper, we study the setup of multiple response variables and a notion of mismatches that generalizes permutations in order to allow for missing matches as well as for one-to-many matches. A two-stage method is proposed under the assumption that most pairs are correctly matched. In the first stage, the regression parameter is estimated by handling mismatches as contaminations, and subsequently the generalized permutation is estimated by a basic variant of matching. The approach is both computationally convenient and equipped with favorable statistical guarantees. Specifically, it is shown that the conditions for permutation recovery become considerably less stringent as the number of responses $m$ per observation increase. Particularly, for $m = \Omega(\log n)$, the required signal-to-noise ratio does no longer depend on the sample size $n$. Numerical results on synthetic and real data are presented to support the main findings of our analysis.

Linear Regression with Sparsely Permuted Data

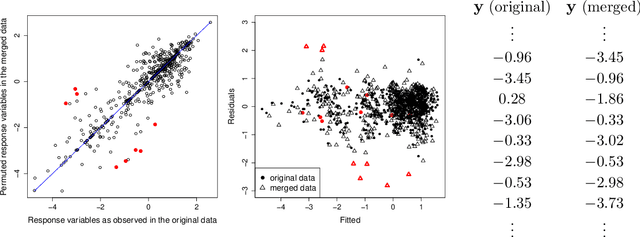
In regression analysis of multivariate data, it is tacitly assumed that response and predictor variables in each observed response-predictor pair correspond to the same entity or unit. In this paper, we consider the situation of "permuted data" in which this basic correspondence has been lost. Several recent papers have considered this situation without further assumptions on the underlying permutation. In applications, the latter is often to known to have additional structure that can be leveraged. Specifically, we herein consider the common scenario of "sparsely permuted data" in which only a small fraction of the data is affected by a mismatch between response and predictors. However, an adverse effect already observed for sparsely permuted data is that the least squares estimator as well as other estimators not accounting for such partial mismatch are inconsistent. One approach studied in detail herein is to treat permuted data as outliers which motivates the use of robust regression formulations to estimate the regression parameter. The resulting estimate can subsequently be used to recover the permutation. A notable benefit of the proposed approach is its computational simplicity given the general lack of procedures for the above problem that are both statistically sound and computationally appealing.