Ask for More Than Bayes Optimal: A Theory of Indecisions for Classification

Selective classification frameworks are useful tools for automated decision making in highly risky scenarios, since they allow for a classifier to only make highly confident decisions, while abstaining from making a decision when it is not confident enough to do so, which is otherwise known as an indecision. For a given level of classification accuracy, we aim to make as many decisions as possible. For many problems, this can be achieved without abstaining from making decisions. But when the problem is hard enough, we show that we can still control the misclassification rate of a classifier up to any user specified level, while only abstaining from the minimum necessary amount of decisions, even if this level of misclassification is smaller than the Bayes optimal error rate. In many problem settings, the user could obtain a dramatic decrease in misclassification while only paying a comparatively small price in terms of indecisions.

Predicting Census Survey Response Rates via Interpretable Nonparametric Additive Models with Structured Interactions

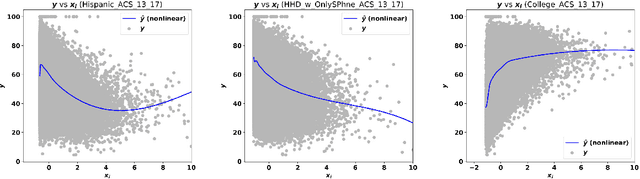
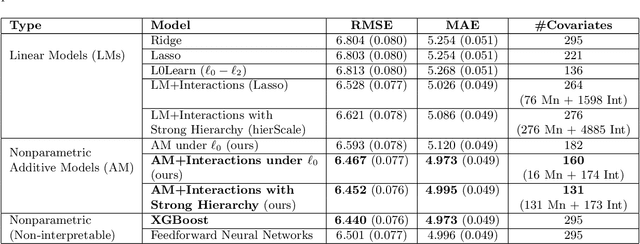
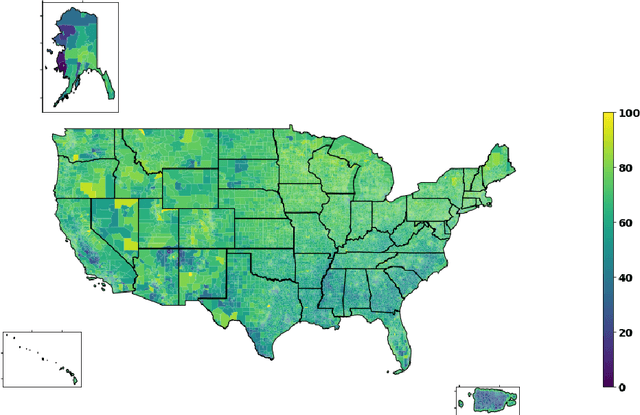
Accurate and interpretable prediction of survey response rates is important from an operational standpoint. The US Census Bureau's well-known ROAM application uses principled statistical models trained on the US Census Planning Database data to identify hard-to-survey areas. An earlier crowdsourcing competition revealed that an ensemble of regression trees led to the best performance in predicting survey response rates; however, the corresponding models could not be adopted for the intended application due to limited interpretability. In this paper, we present new interpretable statistical methods to predict, with high accuracy, response rates in surveys. We study sparse nonparametric additive models with pairwise interactions via $\ell_0$-regularization, as well as hierarchically structured variants that provide enhanced interpretability. Despite strong methodological underpinnings, such models can be computationally challenging -- we present new scalable algorithms for learning these models. We also establish novel non-asymptotic error bounds for the proposed estimators. Experiments based on the US Census Planning Database demonstrate that our methods lead to high-quality predictive models that permit actionable interpretability for different segments of the population. Interestingly, our methods provide significant gains in interpretability without losing in predictive performance to state-of-the-art black-box machine learning methods based on gradient boosting and feedforward neural networks. Our code implementation in python is available at https://github.com/ShibalIbrahim/Additive-Models-with-Structured-Interactions.

Grouped Variable Selection with Discrete Optimization: Computational and Statistical Perspectives

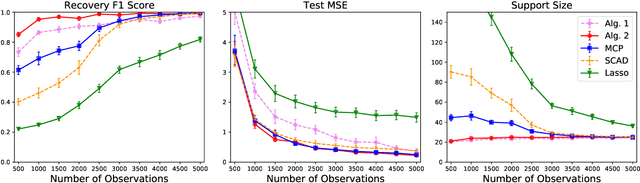
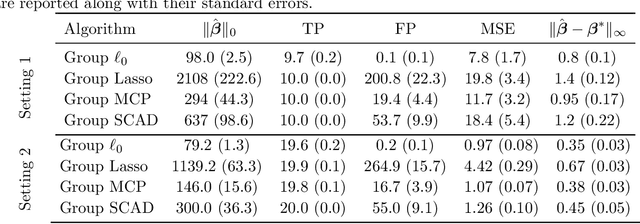
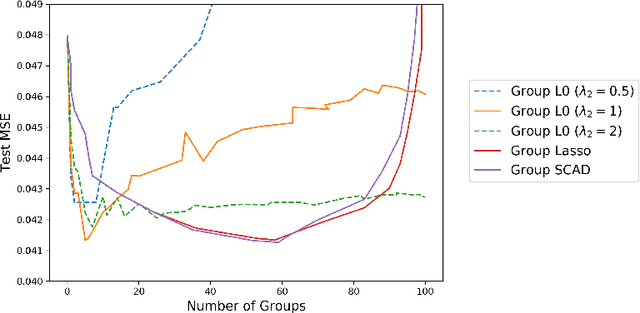
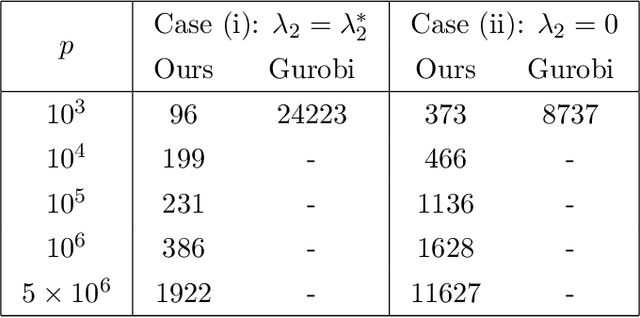
We present a new algorithmic framework for grouped variable selection that is based on discrete mathematical optimization. While there exist several appealing approaches based on convex relaxations and nonconvex heuristics, we focus on optimal solutions for the $\ell_0$-regularized formulation, a problem that is relatively unexplored due to computational challenges. Our methodology covers both high-dimensional linear regression and nonparametric sparse additive modeling with smooth components. Our algorithmic framework consists of approximate and exact algorithms. The approximate algorithms are based on coordinate descent and local search, with runtimes comparable to popular sparse learning algorithms. Our exact algorithm is based on a standalone branch-and-bound (BnB) framework, which can solve the associated mixed integer programming (MIP) problem to certified optimality. By exploiting the problem structure, our custom BnB algorithm can solve to optimality problem instances with $5 \times 10^6$ features in minutes to hours -- over $1000$ times larger than what is currently possible using state-of-the-art commercial MIP solvers. We also explore statistical properties of the $\ell_0$-based estimators. We demonstrate, theoretically and empirically, that our proposed estimators have an edge over popular group-sparse estimators in terms of statistical performance in various regimes.

Subset Selection with Shrinkage: Sparse Linear Modeling when the SNR is low

We study the behavior of a fundamental tool in sparse statistical modeling --the best-subset selection procedure (aka "best-subsets"). Assuming that the underlying linear model is sparse, it is well known, both in theory and in practice, that the best-subsets procedure works extremely well in terms of several statistical metrics (prediction, estimation and variable selection) when the signal to noise ratio (SNR) is high. However, its performance degrades substantially when the SNR is low -- it is outperformed in predictive accuracy by continuous shrinkage methods, such as ridge regression and the Lasso. We explain why this behavior should not come as a surprise, and contend that the original version of the classical best-subsets procedure was, perhaps, not designed to be used in the low SNR regimes. We propose a close cousin of best-subsets, namely, its $\ell_{q}$-regularized version, for $q \in\{1, 2\}$, which (a) mitigates, to a large extent, the poor predictive performance of best-subsets in the low SNR regimes; (b) performs favorably and generally delivers a substantially sparser model when compared to the best predictive models available via ridge regression and the Lasso. Our estimator can be expressed as a solution to a mixed integer second order conic optimization problem and, hence, is amenable to modern computational tools from mathematical optimization. We explore the theoretical properties of the predictive capabilities of the proposed estimator and complement our findings via several numerical experiments.

The Discrete Dantzig Selector: Estimating Sparse Linear Models via Mixed Integer Linear Optimization

We propose a novel high-dimensional linear regression estimator: the Discrete Dantzig Selector, which minimizes the number of nonzero regression coefficients subject to a budget on the maximal absolute correlation between the features and residuals. Motivated by the significant advances in integer optimization over the past 10-15 years, we present a Mixed Integer Linear Optimization (MILO) approach to obtain certifiably optimal global solutions to this nonconvex optimization problem. The current state of algorithmics in integer optimization makes our proposal substantially more computationally attractive than the least squares subset selection framework based on integer quadratic optimization, recently proposed in [8] and the continuous nonconvex quadratic optimization framework of [33]. We propose new discrete first-order methods, which when paired with state-of-the-art MILO solvers, lead to good solutions for the Discrete Dantzig Selector problem for a given computational budget. We illustrate that our integrated approach provides globally optimal solutions in significantly shorter computation times, when compared to off-the-shelf MILO solvers. We demonstrate both theoretically and empirically that in a wide range of regimes the statistical properties of the Discrete Dantzig Selector are superior to those of popular $\ell_{1}$-based approaches. We illustrate that our approach can handle problem instances with p = 10,000 features with certifiable optimality making it a highly scalable combinatorial variable selection approach in sparse linear modeling.