Ask for More Than Bayes Optimal: A Theory of Indecisions for Classification

Selective classification frameworks are useful tools for automated decision making in highly risky scenarios, since they allow for a classifier to only make highly confident decisions, while abstaining from making a decision when it is not confident enough to do so, which is otherwise known as an indecision. For a given level of classification accuracy, we aim to make as many decisions as possible. For many problems, this can be achieved without abstaining from making decisions. But when the problem is hard enough, we show that we can still control the misclassification rate of a classifier up to any user specified level, while only abstaining from the minimum necessary amount of decisions, even if this level of misclassification is smaller than the Bayes optimal error rate. In many problem settings, the user could obtain a dramatic decrease in misclassification while only paying a comparatively small price in terms of indecisions.

Adaptive Mean Estimation in the Hidden Markov sub-Gaussian Mixture Model

We investigate the problem of center estimation in the high dimensional binary sub-Gaussian Mixture Model with Hidden Markov structure on the labels. We first study the limitations of existing results in the high dimensional setting and then propose a minimax optimal procedure for the problem of center estimation. Among other findings, we show that our procedure reaches the optimal rate that is of order $\sqrt{\delta d/n} + d/n$ instead of $\sqrt{d/n} + d/n$ where $\delta \in(0,1)$ is a dependence parameter between labels. Along the way, we also develop an adaptive variant of our procedure that is globally minimax optimal. In order to do so, we rely on a more refined and localized analysis of the estimation risk. Overall, leveraging the hidden Markovian dependence between the labels, we show that it is possible to get a strict improvement of the rates adaptively at almost no cost.

Minimax Supervised Clustering in the Anisotropic Gaussian Mixture Model: A new take on Robust Interpolation

We study the supervised clustering problem under the two-component anisotropic Gaussian mixture model in high dimensions and in the non-asymptotic setting. We first derive a lower and a matching upper bound for the minimax risk of clustering in this framework. We also show that in the high-dimensional regime, the linear discriminant analysis (LDA) classifier turns out to be sub-optimal in the minimax sense. Next, we characterize precisely the risk of $\ell_2$-regularized supervised least squares classifiers. We deduce the fact that the interpolating solution may outperform the regularized classifier, under mild assumptions on the covariance structure of the noise. Our analysis also shows that interpolation can be robust to corruption in the covariance of the noise when the signal is aligned with the "clean" part of the covariance, for the properly defined notion of alignment. To the best of our knowledge, this peculiar phenomenon has not yet been investigated in the rapidly growing literature related to interpolation. We conclude that interpolation is not only benign but can also be optimal, and in some cases robust.

Near-Optimal Model Discrimination with Non-Disclosure

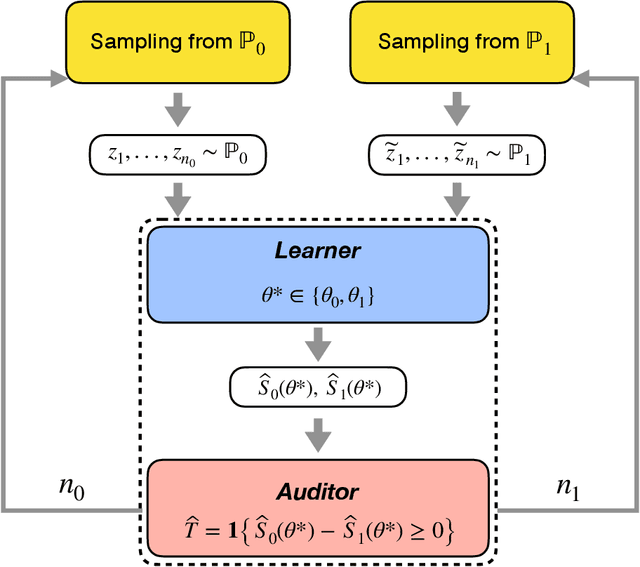
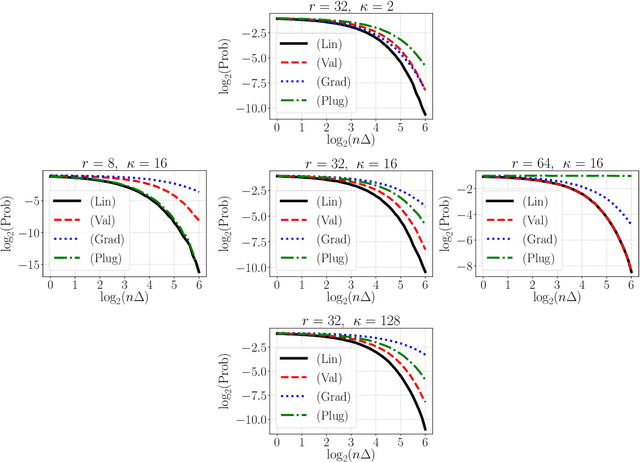
Let $\theta_0,\theta_1 \in \mathbb{R}^d$ be the population risk minimizers associated to some loss $\ell: \mathbb{R}^d \times \mathcal{Z} \to \mathbb{R}$ and two distributions $\mathbb{P}_0,\mathbb{P}_1$ on $\mathcal{Z}$. We pose the following question: Given i.i.d. samples from $\mathbb{P}_0$ and $\mathbb{P}_1$, what sample sizes are sufficient and necessary to distinguish between the two hypotheses $\theta^* = \theta_0$ and $\theta^* = \theta_1$ for given $\theta^* \in \{\theta_0, \theta_1\}$? Making the first steps towards answering this question in full generality, we first consider the case of a well-specified linear model with squared loss. Here we provide matching upper and lower bounds on the sample complexity, showing it to be $\min\{1/\Delta^2, \sqrt{r}/\Delta\}$ up to a constant factor, where $\Delta$ is a measure of separation between $\mathbb{P}_0$ and $\mathbb{P}_1$, and $r$ is the rank of the design covariance matrix. This bound is dimension-independent, and rank-independent for large enough separation. We then extend this result in two directions: (i) for the general parametric setup in asymptotic regime; (ii) for generalized linear models in the small-sample regime $n \le r$ and under weak moment assumptions. In both cases, we derive sample complexity bounds of a similar form, even under misspecification. Our testing procedures only access $\theta^*$ through a certain functional of empirical risk. In addition, the number of observations that allows to reach statistical confidence in our tests does not allow to "resolve" the two models -- that is, recover $\theta_0,\theta_1$ up to $O(\Delta)$ prediction accuracy. These two properties allow to apply our framework in applied tasks where one would like to \textit{identify} a prediction model, which can be proprietary, while guaranteeing that the model cannot be actually \textit{inferred} by the identifying agent.