Stanislav Minsker
Efficient median of means estimator
May 30, 2023Abstract:The goal of this note is to present a modification of the popular median of means estimator that achieves sub-Gaussian deviation bounds with nearly optimal constants under minimal assumptions on the underlying distribution. We build on a recent work on the topic by the author, and prove that desired guarantees can be attained under weaker requirements.
Minimax Supervised Clustering in the Anisotropic Gaussian Mixture Model: A new take on Robust Interpolation
Nov 13, 2021

Abstract:We study the supervised clustering problem under the two-component anisotropic Gaussian mixture model in high dimensions and in the non-asymptotic setting. We first derive a lower and a matching upper bound for the minimax risk of clustering in this framework. We also show that in the high-dimensional regime, the linear discriminant analysis (LDA) classifier turns out to be sub-optimal in the minimax sense. Next, we characterize precisely the risk of $\ell_2$-regularized supervised least squares classifiers. We deduce the fact that the interpolating solution may outperform the regularized classifier, under mild assumptions on the covariance structure of the noise. Our analysis also shows that interpolation can be robust to corruption in the covariance of the noise when the signal is aligned with the "clean" part of the covariance, for the properly defined notion of alignment. To the best of our knowledge, this peculiar phenomenon has not yet been investigated in the rapidly growing literature related to interpolation. We conclude that interpolation is not only benign but can also be optimal, and in some cases robust.
Asymptotic normality of robust risk minimizers
Apr 08, 2020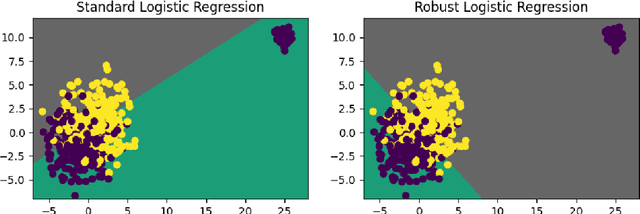
Abstract:This paper investigates asymptotic properties of a class of algorithms that can be viewed as robust analogues of the classical empirical risk minimization. These strategies are based on replacing the usual empirical average by a robust proxy of the mean, such as the median-of-means estimator. It is well known by now that the excess risk of resulting estimators often converges to 0 at the optimal rates under much weaker assumptions than those required by their "classical" counterparts. However, much less is known about asymptotic properties of the estimators themselves, for instance, whether robust analogues of the maximum likelihood estimators are asymptotically efficient. We make a step towards answering these questions and show that for a wide class of parametric problems, minimizers of the appropriately defined robust proxy of the risk converge to the minimizers of the true risk at the same rate, and often have the same asymptotic variance, as the estimators obtained by minimizing the usual empirical risk. Moreover, our results show that robust algorithms based on the so-called "min-max" type procedures in many cases provably outperform, is the asymptotic sense, algorithms based on direct risk minimization.
Excess risk bounds in robust empirical risk minimization
Oct 16, 2019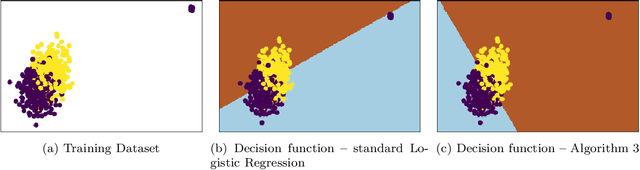
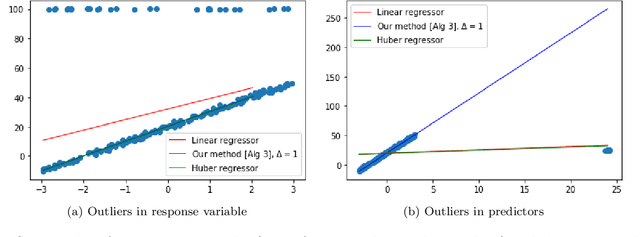
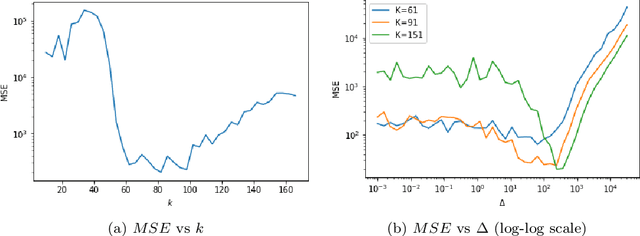
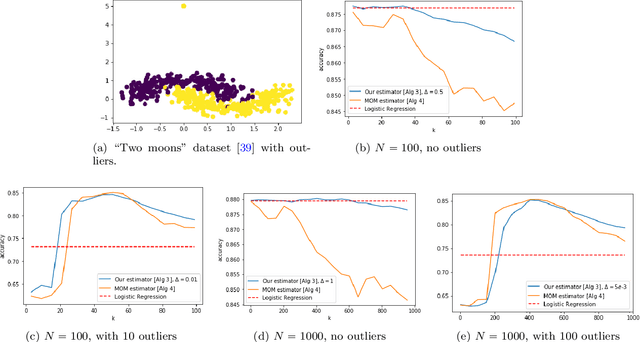
Abstract:This paper investigates robust versions of the general empirical risk minimization algorithm, one of the core techniques underlying modern statistical methods. Success of the empirical risk minimization is based on the fact that for a "well-behaved" stochastic process $\left\{ f(X), \ f\in \mathcal F\right\}$ indexed by a class of functions $f\in \mathcal F$, averages $\frac{1}{N}\sum_{j=1}^N f(X_j)$ evaluated over a sample $X_1,\ldots,X_N$ of i.i.d. copies of $X$ provide good approximation to the expectations $\mathbb E f(X)$ uniformly over large classes $f\in \mathcal F$. However, this might no longer be true if the marginal distributions of the process are heavy-tailed or if the sample contains outliers. We propose a version of empirical risk minimization based on the idea of replacing sample averages by robust proxies of the expectation, and obtain high-confidence bounds for the excess risk of resulting estimators. In particular, we show that the excess risk of robust estimators can converge to $0$ at fast rates with respect to the sample size. We discuss implications of the main results to the linear and logistic regression problems, and evaluate the numerical performance of proposed methods on simulated and real data.
Distributed Statistical Estimation and Rates of Convergence in Normal Approximation
Aug 27, 2018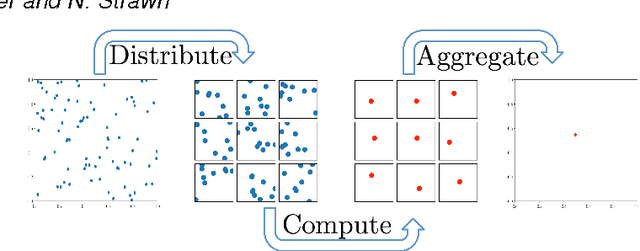
Abstract:This paper presents a class of new algorithms for distributed statistical estimation that exploit divide-and-conquer approach. We show that one of the key benefits of the divide-and-conquer strategy is robustness, an important characteristic for large distributed systems. We establish connections between performance of these distributed algorithms and the rates of convergence in normal approximation, and prove non-asymptotic deviations guarantees, as well as limit theorems, for the resulting estimators. Our techniques are illustrated through several examples: in particular, we obtain new results for the median-of-means estimator, as well as provide performance guarantees for distributed maximum likelihood estimation.
Sub-Gaussian estimators of the mean of a random matrix with heavy-tailed entries
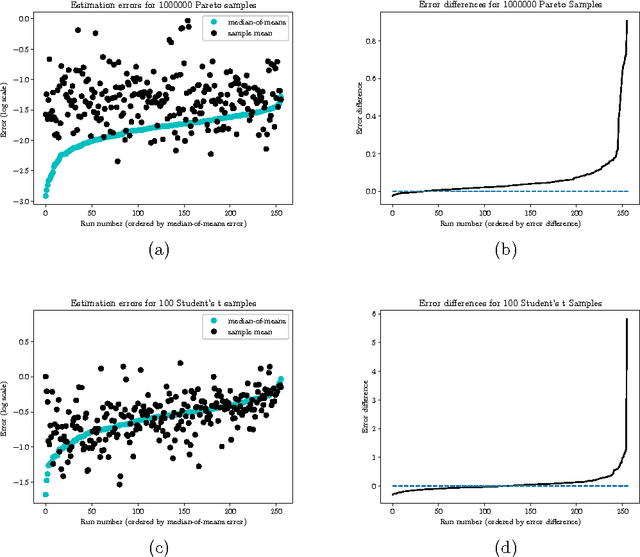
Jun 17, 2018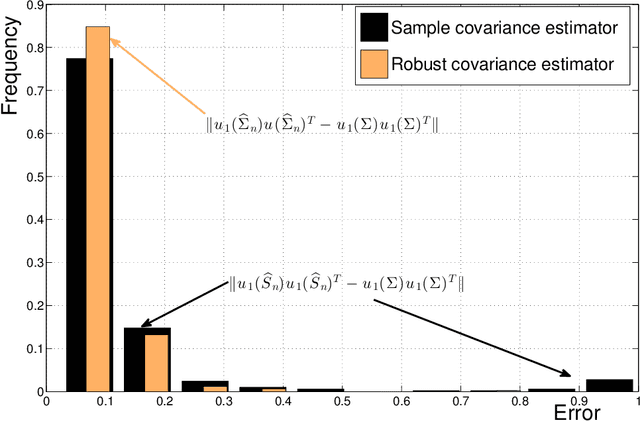
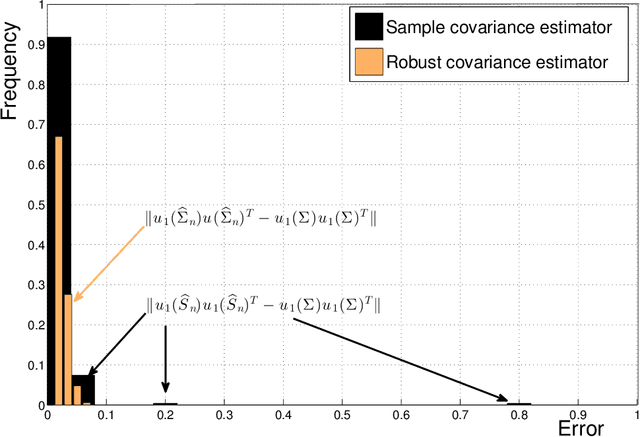
Abstract:Estimation of the covariance matrix has attracted a lot of attention of the statistical research community over the years, partially due to important applications such as Principal Component Analysis. However, frequently used empirical covariance estimator (and its modifications) is very sensitive to outliers in the data. As P. J. Huber wrote in 1964, "...This raises a question which could have been asked already by Gauss, but which was, as far as I know, only raised a few years ago (notably by Tukey): what happens if the true distribution deviates slightly from the assumed normal one? As is now well known, the sample mean then may have a catastrophically bad performance..." Motivated by this question, we develop a new estimator of the (element-wise) mean of a random matrix, which includes covariance estimation problem as a special case. Assuming that the entries of a matrix possess only finite second moment, this new estimator admits sub-Gaussian or sub-exponential concentration around the unknown mean in the operator norm. We will explain the key ideas behind our construction, as well as applications to covariance estimation and matrix completion problems.
Robust and Scalable Bayes via a Median of Subset Posterior Measures
Jun 02, 2016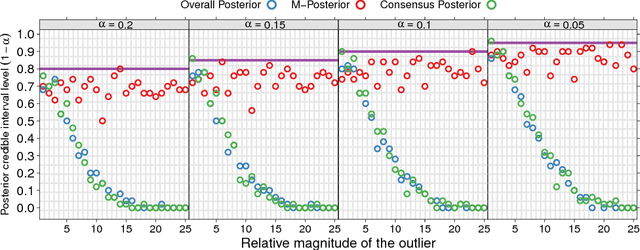
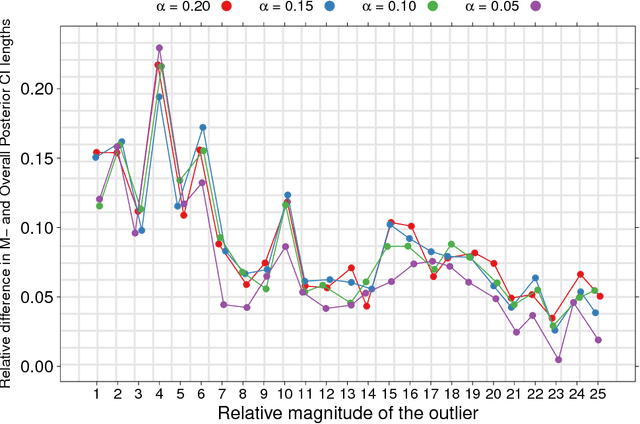
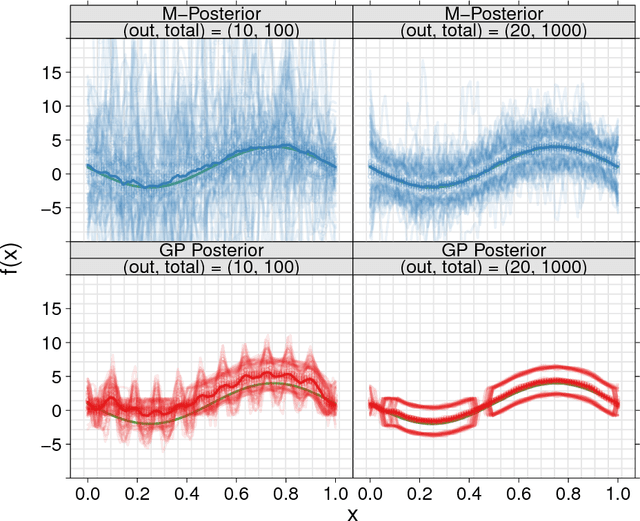
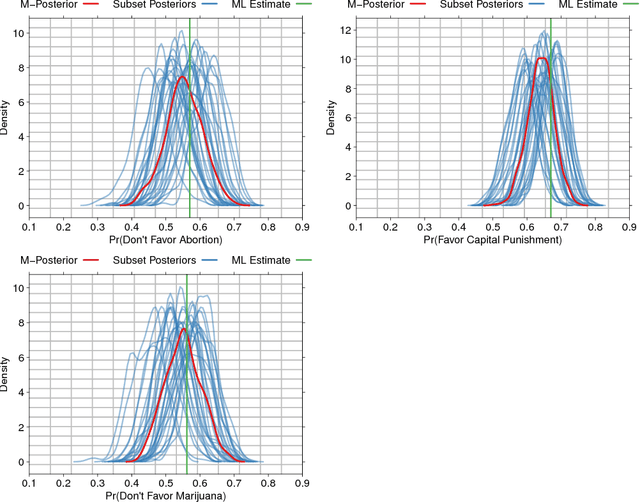
Abstract:We propose a novel approach to Bayesian analysis that is provably robust to outliers in the data and often has computational advantages over standard methods. Our technique is based on splitting the data into non-overlapping subgroups, evaluating the posterior distribution given each independent subgroup, and then combining the resulting measures. The main novelty of our approach is the proposed aggregation step, which is based on the evaluation of a median in the space of probability measures equipped with a suitable collection of distances that can be quickly and efficiently evaluated in practice. We present both theoretical and numerical evidence illustrating the improvements achieved by our method.
Plug-in Approach to Active Learning
Nov 02, 2011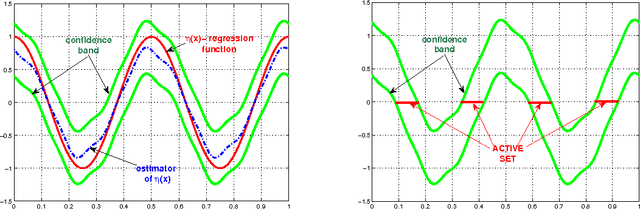

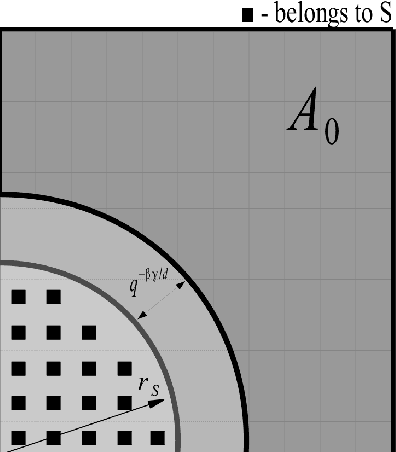
Abstract:We present a new active learning algorithm based on nonparametric estimators of the regression function. Our investigation provides probabilistic bounds for the rates of convergence of the generalization error achievable by proposed method over a broad class of underlying distributions. We also prove minimax lower bounds which show that the obtained rates are almost tight.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge