Machine Learning and the Future of Bayesian Computation

Bayesian models are a powerful tool for studying complex data, allowing the analyst to encode rich hierarchical dependencies and leverage prior information. Most importantly, they facilitate a complete characterization of uncertainty through the posterior distribution. Practical posterior computation is commonly performed via MCMC, which can be computationally infeasible for high dimensional models with many observations. In this article we discuss the potential to improve posterior computation using ideas from machine learning. Concrete future directions are explored in vignettes on normalizing flows, Bayesian coresets, distributed Bayesian inference, and variational inference.

Asynchronous and Distributed Data Augmentation for Massive Data Settings

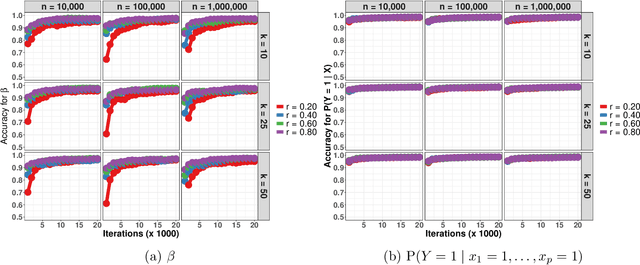
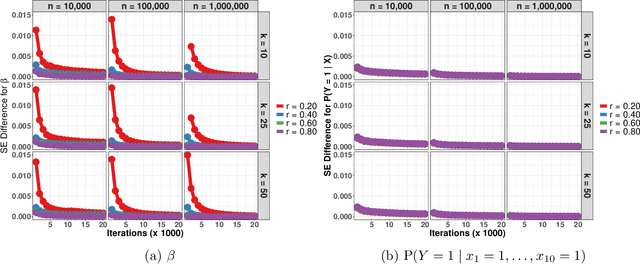
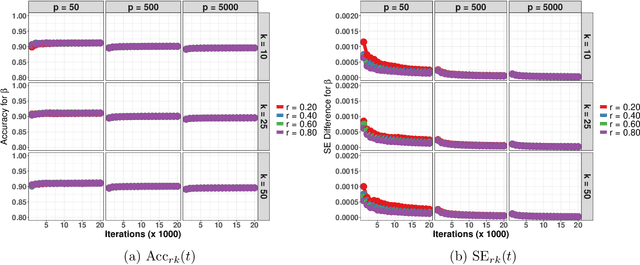
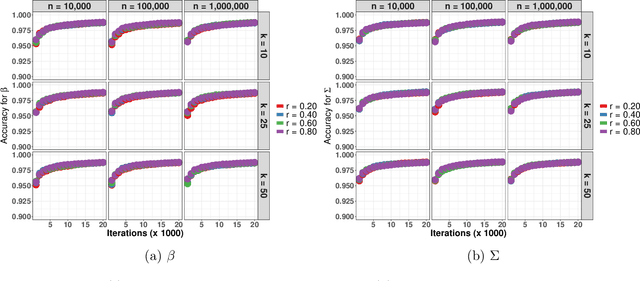
Data augmentation (DA) algorithms are widely used for Bayesian inference due to their simplicity. In massive data settings, however, DA algorithms are prohibitively slow because they pass through the full data in any iteration, imposing serious restrictions on their usage despite the advantages. Addressing this problem, we develop a framework for extending any DA that exploits asynchronous and distributed computing. The extended DA algorithm is indexed by a parameter $r \in (0, 1)$ and is called Asynchronous and Distributed (AD) DA with the original DA as its parent. Any ADDA starts by dividing the full data into $k$ smaller disjoint subsets and storing them on $k$ processes, which could be machines or processors. Every iteration of ADDA augments only an $r$-fraction of the $k$ data subsets with some positive probability and leaves the remaining $(1-r)$-fraction of the augmented data unchanged. The parameter draws are obtained using the $r$-fraction of new and $(1-r)$-fraction of old augmented data. For many choices of $k$ and $r$, the fractional updates of ADDA lead to a significant speed-up over the parent DA in massive data settings, and it reduces to the distributed version of its parent DA when $r=1$. We show that the ADDA Markov chain is Harris ergodic with the desired stationary distribution under mild conditions on the parent DA algorithm. We demonstrate the numerical advantages of the ADDA in three representative examples corresponding to different kinds of massive data settings encountered in applications. In all these examples, our DA generalization is significantly faster than its parent DA algorithm for all the choices of $k$ and $r$. We also establish geometric ergodicity of the ADDA Markov chain for all three examples, which in turn yields asymptotically valid standard errors for estimates of desired posterior quantities.

An Asynchronous Distributed Expectation Maximization Algorithm For Massive Data: The DEM Algorithm

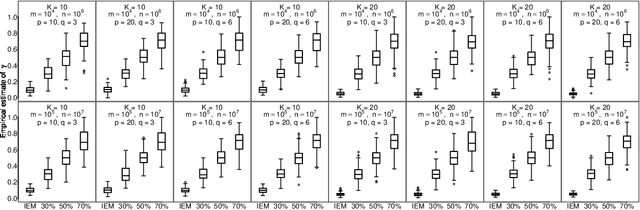
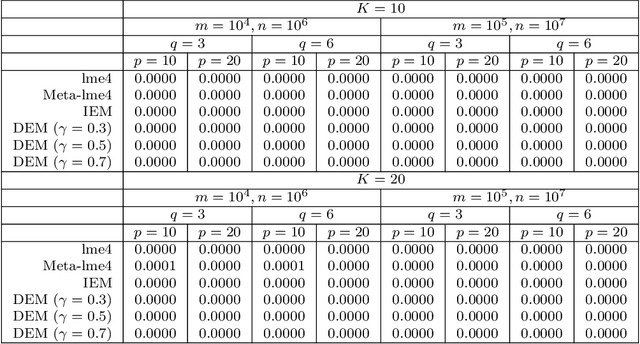
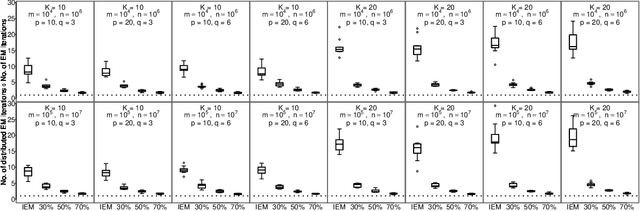
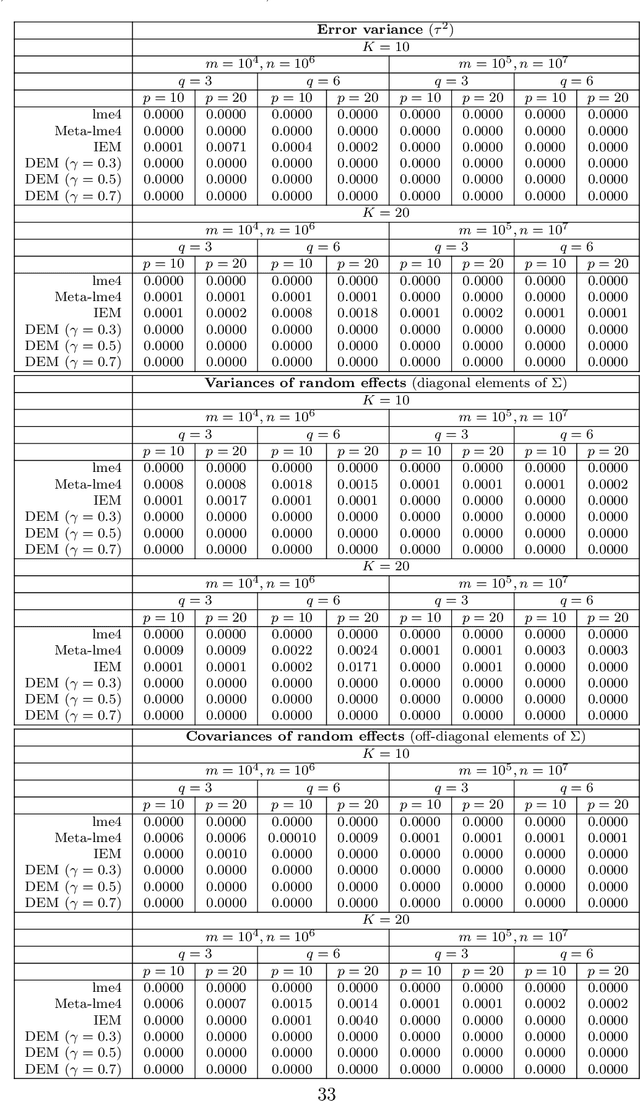
The family of Expectation-Maximization (EM) algorithms provides a general approach to fitting flexible models for large and complex data. The expectation (E) step of EM-type algorithms is time-consuming in massive data applications because it requires multiple passes through the full data. We address this problem by proposing an asynchronous and distributed generalization of the EM called the Distributed EM (DEM). Using DEM, existing EM-type algorithms are easily extended to massive data settings by exploiting the divide-and-conquer technique and widely available computing power, such as grid computing. The DEM algorithm reserves two groups of computing processes called \emph{workers} and \emph{managers} for performing the E step and the maximization step (M step), respectively. The samples are randomly partitioned into a large number of disjoint subsets and are stored on the worker processes. The E step of DEM algorithm is performed in parallel on all the workers, and every worker communicates its results to the managers at the end of local E step. The managers perform the M step after they have received results from a $\gamma$-fraction of the workers, where $\gamma$ is a fixed constant in $(0, 1]$. The sequence of parameter estimates generated by the DEM algorithm retains the attractive properties of EM: convergence of the sequence of parameter estimates to a local mode and linear global rate of convergence. Across diverse simulations focused on linear mixed-effects models, the DEM algorithm is significantly faster than competing EM-type algorithms while having a similar accuracy. The DEM algorithm maintains its superior empirical performance on a movie ratings database consisting of 10 million ratings.

Robust and Scalable Bayes via a Median of Subset Posterior Measures

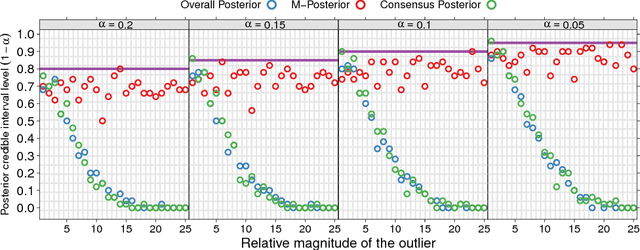
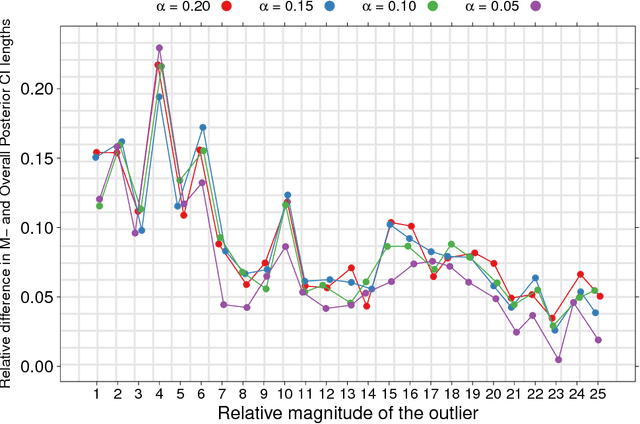
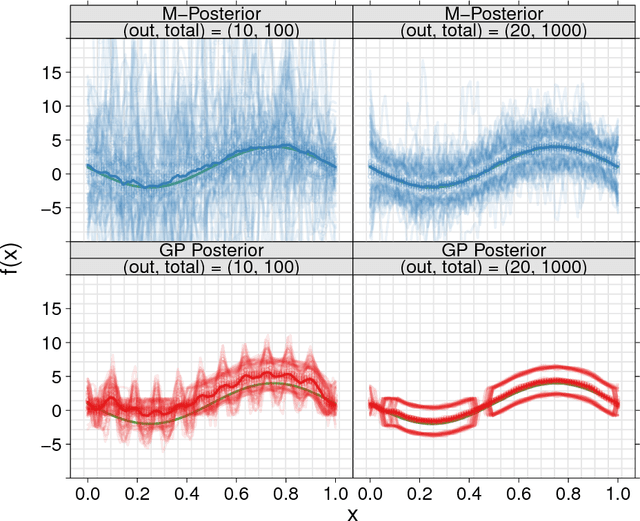
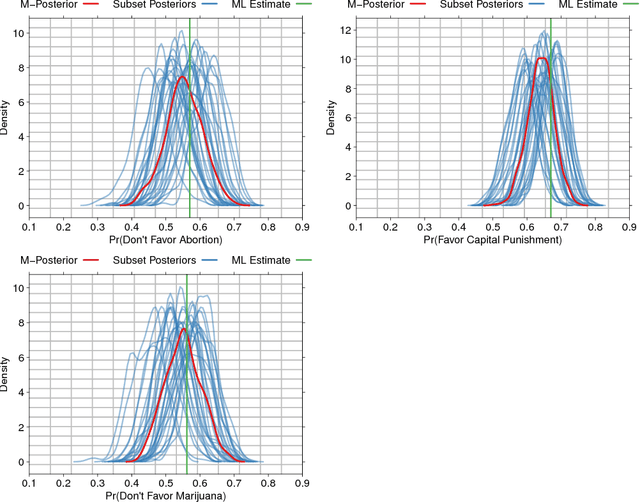
We propose a novel approach to Bayesian analysis that is provably robust to outliers in the data and often has computational advantages over standard methods. Our technique is based on splitting the data into non-overlapping subgroups, evaluating the posterior distribution given each independent subgroup, and then combining the resulting measures. The main novelty of our approach is the proposed aggregation step, which is based on the evaluation of a median in the space of probability measures equipped with a suitable collection of distances that can be quickly and efficiently evaluated in practice. We present both theoretical and numerical evidence illustrating the improvements achieved by our method.