Scalable and non-iterative graphical model estimation

Graphical models have found widespread applications in many areas of modern statistics and machine learning. Iterative Proportional Fitting (IPF) and its variants have become the default method for undirected graphical model estimation, and are thus ubiquitous in the field. As the IPF is an iterative approach, it is not always readily scalable to modern high-dimensional data regimes. In this paper we propose a novel and fast non-iterative method for positive definite graphical model estimation in high dimensions, one that directly addresses the shortcomings of IPF and its variants. In addition, the proposed method has a number of other attractive properties. First, we show formally that as the dimension p grows, the proportion of graphs for which the proposed method will outperform the state-of-the-art in terms of computational complexity and performance tends to 1, affirming its efficacy in modern settings. Second, the proposed approach can be readily combined with scalable non-iterative thresholding-based methods for high-dimensional sparsity selection. Third, the proposed method has high-dimensional statistical guarantees. Moreover, our numerical experiments also show that the proposed method achieves scalability without compromising on statistical precision. Fourth, unlike the IPF, which depends on the Gaussian likelihood, the proposed method is much more robust.

Multi-Granularity Detector for Vulnerability Fixes

With the increasing reliance on Open Source Software, users are exposed to third-party library vulnerabilities. Software Composition Analysis (SCA) tools have been created to alert users of such vulnerabilities. SCA requires the identification of vulnerability-fixing commits. Prior works have proposed methods that can automatically identify such vulnerability-fixing commits. However, identifying such commits is highly challenging, as only a very small minority of commits are vulnerability fixing. Moreover, code changes can be noisy and difficult to analyze. We observe that noise can occur at different levels of detail, making it challenging to detect vulnerability fixes accurately. To address these challenges and boost the effectiveness of prior works, we propose MiDas (Multi-Granularity Detector for Vulnerability Fixes). Unique from prior works, Midas constructs different neural networks for each level of code change granularity, corresponding to commit-level, file-level, hunk-level, and line-level, following their natural organization. It then utilizes an ensemble model that combines all base models to generate the final prediction. This design allows MiDas to better handle the noisy and highly imbalanced nature of vulnerability-fixing commit data. Additionally, to reduce the human effort required to inspect code changes, we have designed an effort-aware adjustment for Midas's outputs based on commit length. The evaluation results demonstrate that MiDas outperforms the current state-of-the-art baseline in terms of AUC by 4.9% and 13.7% on Java and Python-based datasets, respectively. Furthermore, in terms of two effort-aware metrics, EffortCost@L and Popt@L, MiDas also outperforms the state-of-the-art baseline, achieving improvements of up to 28.2% and 15.9% on Java, and 60% and 51.4% on Python, respectively.

Asynchronous and Distributed Data Augmentation for Massive Data Settings

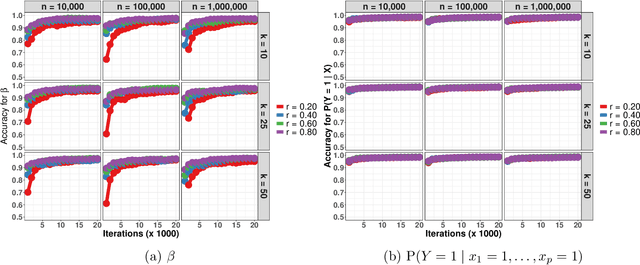
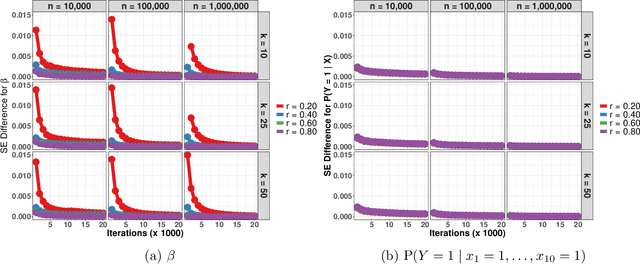
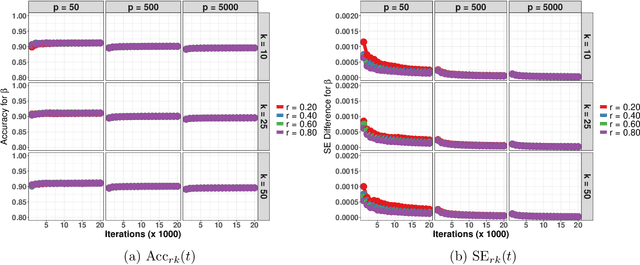
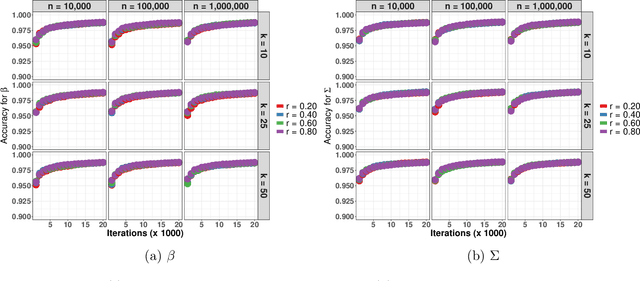
Data augmentation (DA) algorithms are widely used for Bayesian inference due to their simplicity. In massive data settings, however, DA algorithms are prohibitively slow because they pass through the full data in any iteration, imposing serious restrictions on their usage despite the advantages. Addressing this problem, we develop a framework for extending any DA that exploits asynchronous and distributed computing. The extended DA algorithm is indexed by a parameter $r \in (0, 1)$ and is called Asynchronous and Distributed (AD) DA with the original DA as its parent. Any ADDA starts by dividing the full data into $k$ smaller disjoint subsets and storing them on $k$ processes, which could be machines or processors. Every iteration of ADDA augments only an $r$-fraction of the $k$ data subsets with some positive probability and leaves the remaining $(1-r)$-fraction of the augmented data unchanged. The parameter draws are obtained using the $r$-fraction of new and $(1-r)$-fraction of old augmented data. For many choices of $k$ and $r$, the fractional updates of ADDA lead to a significant speed-up over the parent DA in massive data settings, and it reduces to the distributed version of its parent DA when $r=1$. We show that the ADDA Markov chain is Harris ergodic with the desired stationary distribution under mild conditions on the parent DA algorithm. We demonstrate the numerical advantages of the ADDA in three representative examples corresponding to different kinds of massive data settings encountered in applications. In all these examples, our DA generalization is significantly faster than its parent DA algorithm for all the choices of $k$ and $r$. We also establish geometric ergodicity of the ADDA Markov chain for all three examples, which in turn yields asymptotically valid standard errors for estimates of desired posterior quantities.