Scalable and non-iterative graphical model estimation

Graphical models have found widespread applications in many areas of modern statistics and machine learning. Iterative Proportional Fitting (IPF) and its variants have become the default method for undirected graphical model estimation, and are thus ubiquitous in the field. As the IPF is an iterative approach, it is not always readily scalable to modern high-dimensional data regimes. In this paper we propose a novel and fast non-iterative method for positive definite graphical model estimation in high dimensions, one that directly addresses the shortcomings of IPF and its variants. In addition, the proposed method has a number of other attractive properties. First, we show formally that as the dimension p grows, the proportion of graphs for which the proposed method will outperform the state-of-the-art in terms of computational complexity and performance tends to 1, affirming its efficacy in modern settings. Second, the proposed approach can be readily combined with scalable non-iterative thresholding-based methods for high-dimensional sparsity selection. Third, the proposed method has high-dimensional statistical guarantees. Moreover, our numerical experiments also show that the proposed method achieves scalability without compromising on statistical precision. Fourth, unlike the IPF, which depends on the Gaussian likelihood, the proposed method is much more robust.

The data augmentation algorithm

The data augmentation (DA) algorithms are popular Markov chain Monte Carlo (MCMC) algorithms often used for sampling from intractable probability distributions. This review article comprehensively surveys DA MCMC algorithms, highlighting their theoretical foundations, methodological implementations, and diverse applications in frequentist and Bayesian statistics. The article discusses tools for studying the convergence properties of DA algorithms. Furthermore, it contains various strategies for accelerating the speed of convergence of the DA algorithms, different extensions of DA algorithms and outlines promising directions for future research. This paper aims to serve as a resource for researchers and practitioners seeking to leverage data augmentation techniques in MCMC algorithms by providing key insights and synthesizing recent developments.

Asynchronous and Distributed Data Augmentation for Massive Data Settings

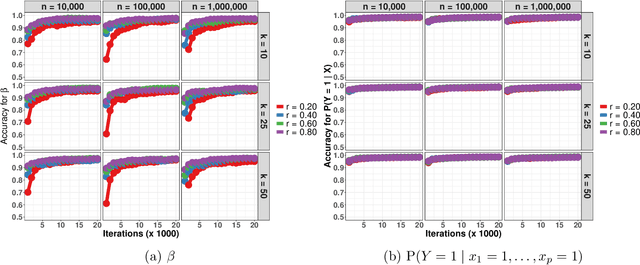
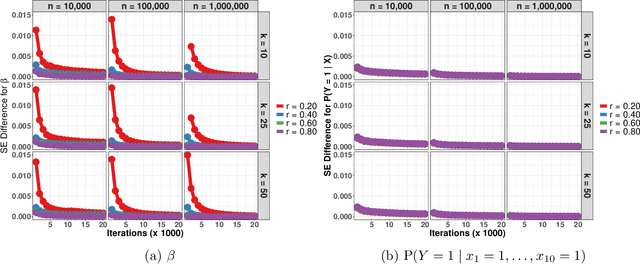
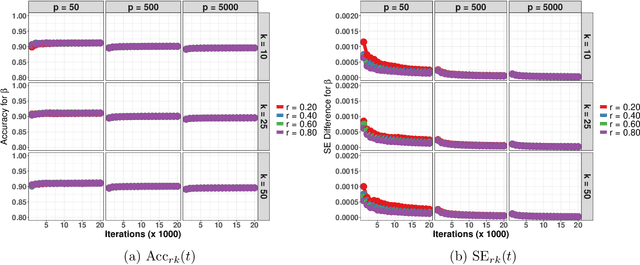
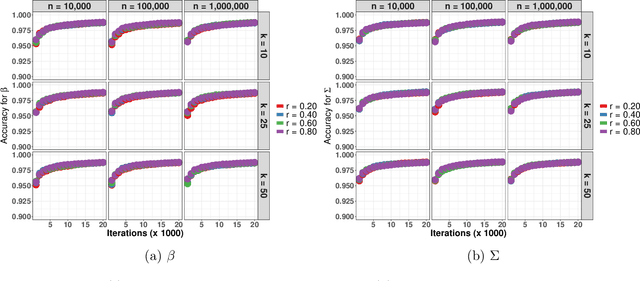
Data augmentation (DA) algorithms are widely used for Bayesian inference due to their simplicity. In massive data settings, however, DA algorithms are prohibitively slow because they pass through the full data in any iteration, imposing serious restrictions on their usage despite the advantages. Addressing this problem, we develop a framework for extending any DA that exploits asynchronous and distributed computing. The extended DA algorithm is indexed by a parameter $r \in (0, 1)$ and is called Asynchronous and Distributed (AD) DA with the original DA as its parent. Any ADDA starts by dividing the full data into $k$ smaller disjoint subsets and storing them on $k$ processes, which could be machines or processors. Every iteration of ADDA augments only an $r$-fraction of the $k$ data subsets with some positive probability and leaves the remaining $(1-r)$-fraction of the augmented data unchanged. The parameter draws are obtained using the $r$-fraction of new and $(1-r)$-fraction of old augmented data. For many choices of $k$ and $r$, the fractional updates of ADDA lead to a significant speed-up over the parent DA in massive data settings, and it reduces to the distributed version of its parent DA when $r=1$. We show that the ADDA Markov chain is Harris ergodic with the desired stationary distribution under mild conditions on the parent DA algorithm. We demonstrate the numerical advantages of the ADDA in three representative examples corresponding to different kinds of massive data settings encountered in applications. In all these examples, our DA generalization is significantly faster than its parent DA algorithm for all the choices of $k$ and $r$. We also establish geometric ergodicity of the ADDA Markov chain for all three examples, which in turn yields asymptotically valid standard errors for estimates of desired posterior quantities.

Optimization Methods for Sparse Pseudo-Likelihood Graphical Model Selection

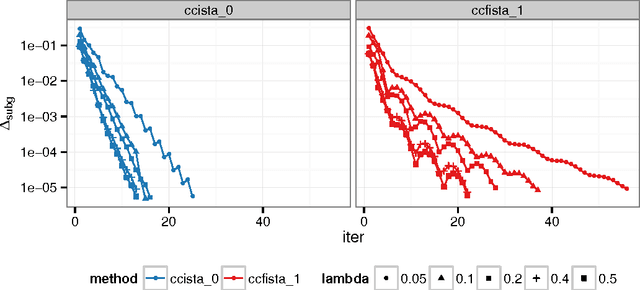
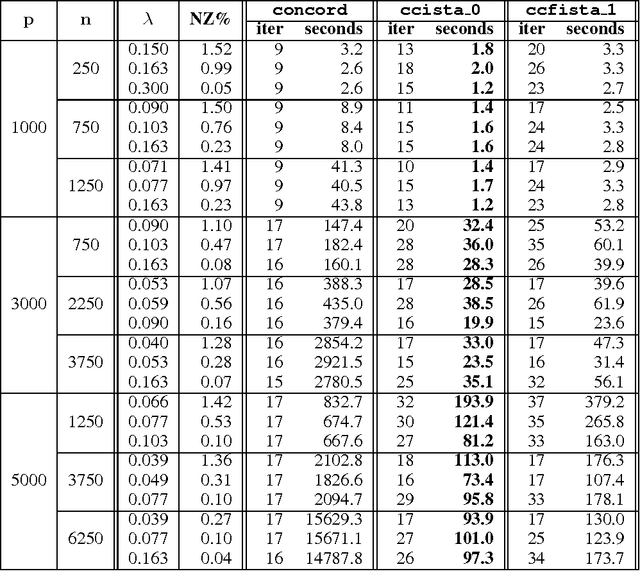
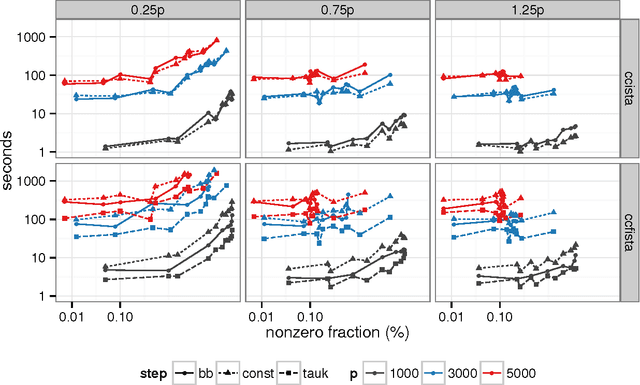
Sparse high dimensional graphical model selection is a popular topic in contemporary machine learning. To this end, various useful approaches have been proposed in the context of $\ell_1$-penalized estimation in the Gaussian framework. Though many of these inverse covariance estimation approaches are demonstrably scalable and have leveraged recent advances in convex optimization, they still depend on the Gaussian functional form. To address this gap, a convex pseudo-likelihood based partial correlation graph estimation method (CONCORD) has been recently proposed. This method uses coordinate-wise minimization of a regression based pseudo-likelihood, and has been shown to have robust model selection properties in comparison with the Gaussian approach. In direct contrast to the parallel work in the Gaussian setting however, this new convex pseudo-likelihood framework has not leveraged the extensive array of methods that have been proposed in the machine learning literature for convex optimization. In this paper, we address this crucial gap by proposing two proximal gradient methods (CONCORD-ISTA and CONCORD-FISTA) for performing $\ell_1$-regularized inverse covariance matrix estimation in the pseudo-likelihood framework. We present timing comparisons with coordinate-wise minimization and demonstrate that our approach yields tremendous payoffs for $\ell_1$-penalized partial correlation graph estimation outside the Gaussian setting, thus yielding the fastest and most scalable approach for such problems. We undertake a theoretical analysis of our approach and rigorously demonstrate convergence, and also derive rates thereof.

A convex pseudo-likelihood framework for high dimensional partial correlation estimation with convergence guarantees

Sparse high dimensional graphical model selection is a topic of much interest in modern day statistics. A popular approach is to apply l1-penalties to either (1) parametric likelihoods, or, (2) regularized regression/pseudo-likelihoods, with the latter having the distinct advantage that they do not explicitly assume Gaussianity. As none of the popular methods proposed for solving pseudo-likelihood based objective functions have provable convergence guarantees, it is not clear if corresponding estimators exist or are even computable, or if they actually yield correct partial correlation graphs. This paper proposes a new pseudo-likelihood based graphical model selection method that aims to overcome some of the shortcomings of current methods, but at the same time retain all their respective strengths. In particular, we introduce a novel framework that leads to a convex formulation of the partial covariance regression graph problem, resulting in an objective function comprised of quadratic forms. The objective is then optimized via a coordinate-wise approach. The specific functional form of the objective function facilitates rigorous convergence analysis leading to convergence guarantees; an important property that cannot be established using standard results, when the dimension is larger than the sample size, as is often the case in high dimensional applications. These convergence guarantees ensure that estimators are well-defined under very general conditions, and are always computable. In addition, the approach yields estimators that have good large sample properties and also respect symmetry. Furthermore, application to simulated/real data, timing comparisons and numerical convergence is demonstrated. We also present a novel unifying framework that places all graphical pseudo-likelihood methods as special cases of a more general formulation, leading to important insights.