Learning Massive-scale Partial Correlation Networks in Clinical Multi-omics Studies with HP-ACCORD

Graphical model estimation from modern multi-omics data requires a balance between statistical estimation performance and computational scalability. We introduce a novel pseudolikelihood-based graphical model framework that reparameterizes the target precision matrix while preserving sparsity pattern and estimates it by minimizing an $\ell_1$-penalized empirical risk based on a new loss function. The proposed estimator maintains estimation and selection consistency in various metrics under high-dimensional assumptions. The associated optimization problem allows for a provably fast computation algorithm using a novel operator-splitting approach and communication-avoiding distributed matrix multiplication. A high-performance computing implementation of our framework was tested in simulated data with up to one million variables demonstrating complex dependency structures akin to biological networks. Leveraging this scalability, we estimated partial correlation network from a dual-omic liver cancer data set. The co-expression network estimated from the ultrahigh-dimensional data showed superior specificity in prioritizing key transcription factors and co-activators by excluding the impact of epigenomic regulation, demonstrating the value of computational scalability in multi-omic data analysis. %derived from the gene expression data.

Learning Gaussian Graphical Models with Latent Confounders

Gaussian Graphical models (GGM) are widely used to estimate the network structures in many applications ranging from biology to finance. In practice, data is often corrupted by latent confounders which biases inference of the underlying true graphical structure. In this paper, we compare and contrast two strategies for inference in graphical models with latent confounders: Gaussian graphical models with latent variables (LVGGM) and PCA-based removal of confounding (PCA+GGM). While these two approaches have similar goals, they are motivated by different assumptions about confounding. In this paper, we explore the connection between these two approaches and propose a new method, which combines the strengths of these two approaches. We prove the consistency and convergence rate for the PCA-based method and use these results to provide guidance about when to use each method. We demonstrate the effectiveness of our methodology using both simulations and in two real-world applications.

Partial Separability and Functional Graphical Models for Multivariate Gaussian Processes

The covariance structure of multivariate functional data can be highly complex, especially if the multivariate dimension is large, making extension of statistical methods for standard multivariate data to the functional data setting quite challenging. For example, Gaussian graphical models have recently been extended to the setting of multivariate functional data by applying multivariate methods to the coefficients of truncated basis expansions. However, a key difficulty compared to multivariate data is that the covariance operator is compact, and thus not invertible. The methodology in this paper addresses the general problem of covariance modeling for multivariate functional data, and functional Gaussian graphical models in particular. As a first step, a new notion of separability for multivariate functional data is proposed, termed partial separability, leading to a novel Karhunen-Lo\`eve-type expansion for such data. Next, the partial separability structure is shown to be particularly useful in order to provide a well-defined Gaussian graphical model that can be identified with a sequence of finite-dimensional graphical models, each of fixed dimension. This motivates a simple and efficient estimation procedure through application of the joint graphical lasso. Empirical performance of the method for graphical model estimation is assessed through simulation and analysis of functional brain connectivity during a motor task.

Distributionally Robust Formulation and Model Selection for the Graphical Lasso

Building on a recent framework for distributionally robust optimization in machine learning, we develop a similar framework for estimation of the inverse covariance matrix for multivariate data. We provide a novel notion of a Wasserstein ambiguity set specifically tailored to this estimation problem, from which we obtain a representation for a tractable class of regularized estimators. Special cases include penalized likelihood estimators for Gaussian data, specifically the graphical lasso estimator. As a consequence of this formulation, a natural relationship arises between the radius of the Wasserstein ambiguity set and the regularization parameter in the estimation problem. Using this relationship, one can directly control the level of robustness of the estimation procedure by specifying a desired level of confidence with which the ambiguity set contains a distribution with the true population covariance. Furthermore, a unique feature of our formulation is that the radius can be expressed in closed-form as a function of the ordinary sample covariance matrix. Taking advantage of this finding, we develop a simple algorithm to determine a regularization parameter for graphical lasso, using only the bootstrapped sample covariance matrices, meaning that computationally expensive repeated evaluation of the graphical lasso algorithm is not necessary. Alternatively, the distributionally robust formulation can also quantify the robustness of the corresponding estimator if one uses an off-the-shelf method such as cross-validation. Finally, we numerically study the obtained regularization criterion and analyze the robustness of other automated tuning procedures used in practice.

Communication-Avoiding Optimization Methods for Distributed Massive-Scale Sparse Inverse Covariance Estimation

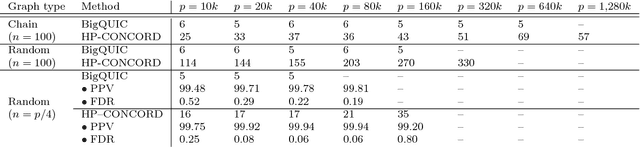
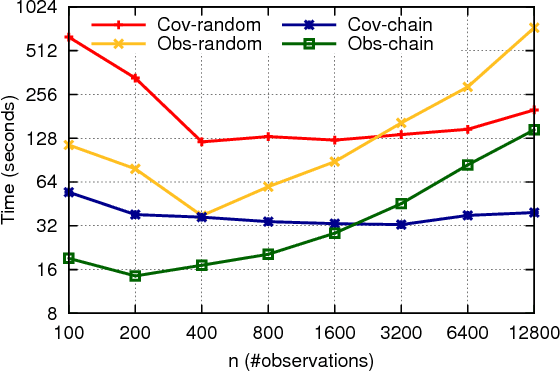
Across a variety of scientific disciplines, sparse inverse covariance estimation is a popular tool for capturing the underlying dependency relationships in multivariate data. Unfortunately, most estimators are not scalable enough to handle the sizes of modern high-dimensional data sets (often on the order of terabytes), and assume Gaussian samples. To address these deficiencies, we introduce HP-CONCORD, a highly scalable optimization method for estimating a sparse inverse covariance matrix based on a regularized pseudolikelihood framework, without assuming Gaussianity. Our parallel proximal gradient method uses a novel communication-avoiding linear algebra algorithm and runs across a multi-node cluster with up to 1k nodes (24k cores), achieving parallel scalability on problems with up to ~819 billion parameters (1.28 million dimensions); even on a single node, HP-CONCORD demonstrates scalability, outperforming a state-of-the-art method. We also use HP-CONCORD to estimate the underlying dependency structure of the brain from fMRI data, and use the result to identify functional regions automatically. The results show good agreement with a clustering from the neuroscience literature.

Revealing Fundamental Physics from the Daya Bay Neutrino Experiment using Deep Neural Networks

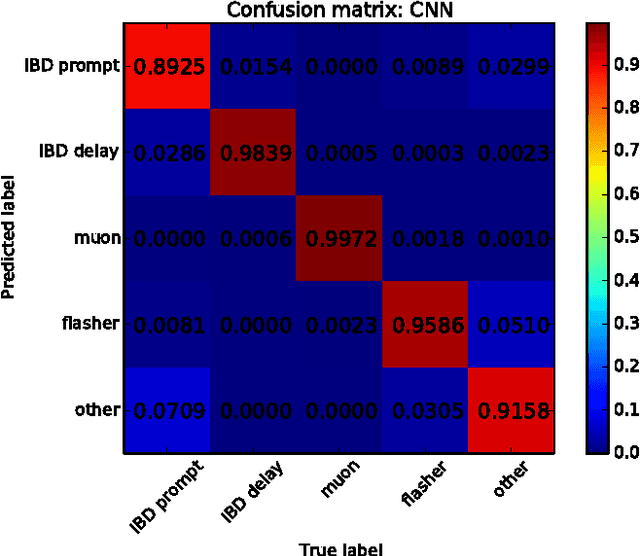
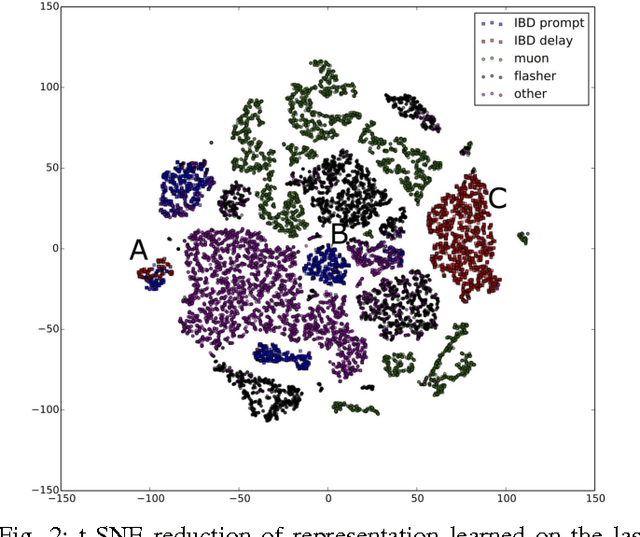
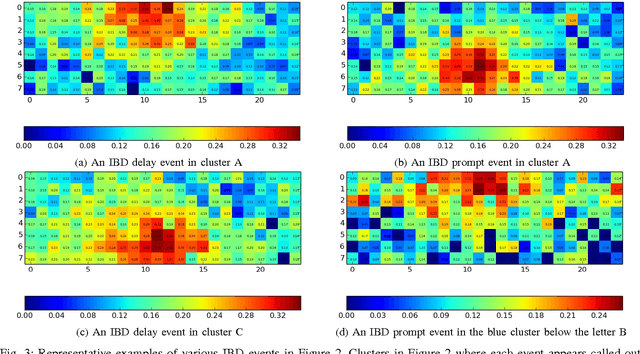
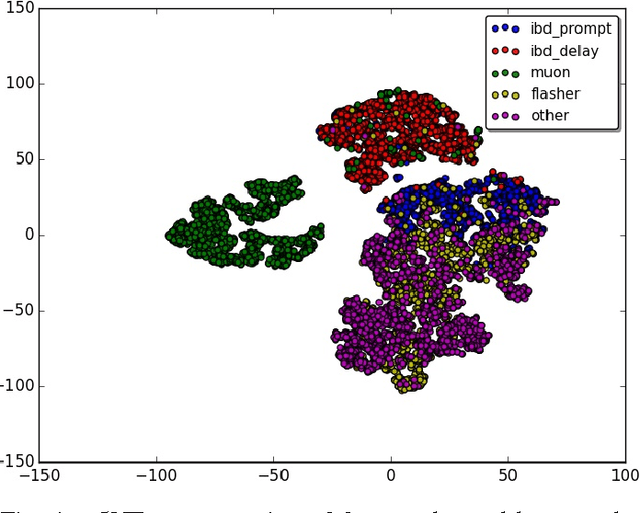
Experiments in particle physics produce enormous quantities of data that must be analyzed and interpreted by teams of physicists. This analysis is often exploratory, where scientists are unable to enumerate the possible types of signal prior to performing the experiment. Thus, tools for summarizing, clustering, visualizing and classifying high-dimensional data are essential. In this work, we show that meaningful physical content can be revealed by transforming the raw data into a learned high-level representation using deep neural networks, with measurements taken at the Daya Bay Neutrino Experiment as a case study. We further show how convolutional deep neural networks can provide an effective classification filter with greater than 97% accuracy across different classes of physics events, significantly better than other machine learning approaches.

Optimization Methods for Sparse Pseudo-Likelihood Graphical Model Selection

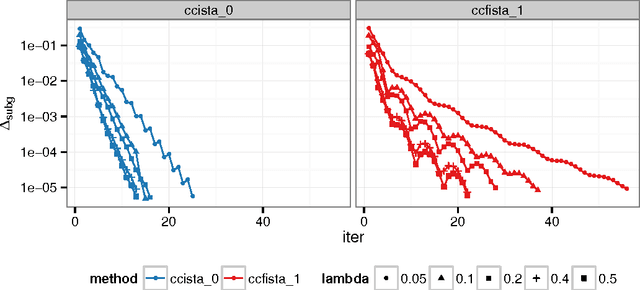
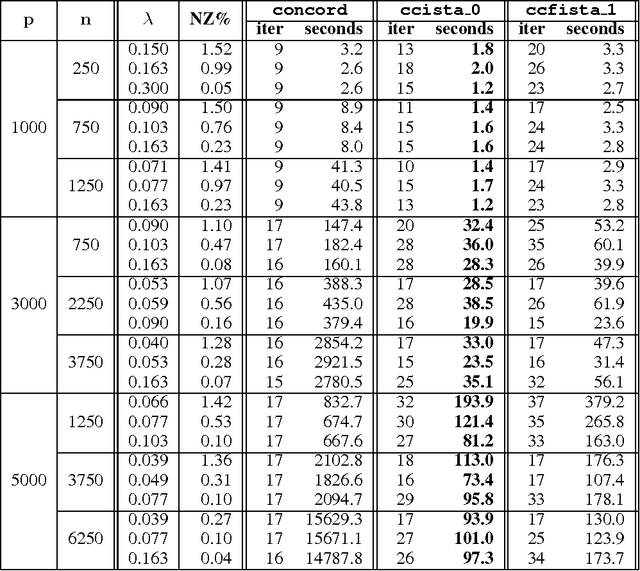
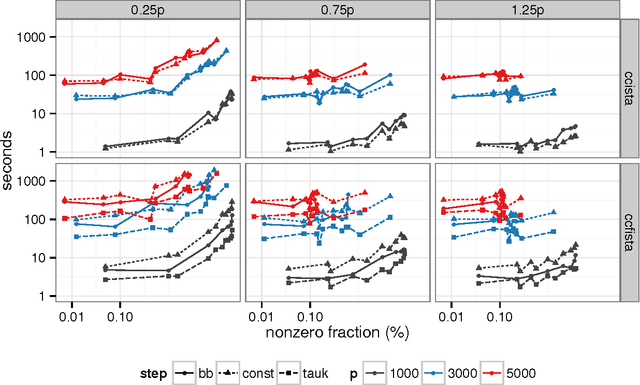
Sparse high dimensional graphical model selection is a popular topic in contemporary machine learning. To this end, various useful approaches have been proposed in the context of $\ell_1$-penalized estimation in the Gaussian framework. Though many of these inverse covariance estimation approaches are demonstrably scalable and have leveraged recent advances in convex optimization, they still depend on the Gaussian functional form. To address this gap, a convex pseudo-likelihood based partial correlation graph estimation method (CONCORD) has been recently proposed. This method uses coordinate-wise minimization of a regression based pseudo-likelihood, and has been shown to have robust model selection properties in comparison with the Gaussian approach. In direct contrast to the parallel work in the Gaussian setting however, this new convex pseudo-likelihood framework has not leveraged the extensive array of methods that have been proposed in the machine learning literature for convex optimization. In this paper, we address this crucial gap by proposing two proximal gradient methods (CONCORD-ISTA and CONCORD-FISTA) for performing $\ell_1$-regularized inverse covariance matrix estimation in the pseudo-likelihood framework. We present timing comparisons with coordinate-wise minimization and demonstrate that our approach yields tremendous payoffs for $\ell_1$-penalized partial correlation graph estimation outside the Gaussian setting, thus yielding the fastest and most scalable approach for such problems. We undertake a theoretical analysis of our approach and rigorously demonstrate convergence, and also derive rates thereof.

A convex pseudo-likelihood framework for high dimensional partial correlation estimation with convergence guarantees

Sparse high dimensional graphical model selection is a topic of much interest in modern day statistics. A popular approach is to apply l1-penalties to either (1) parametric likelihoods, or, (2) regularized regression/pseudo-likelihoods, with the latter having the distinct advantage that they do not explicitly assume Gaussianity. As none of the popular methods proposed for solving pseudo-likelihood based objective functions have provable convergence guarantees, it is not clear if corresponding estimators exist or are even computable, or if they actually yield correct partial correlation graphs. This paper proposes a new pseudo-likelihood based graphical model selection method that aims to overcome some of the shortcomings of current methods, but at the same time retain all their respective strengths. In particular, we introduce a novel framework that leads to a convex formulation of the partial covariance regression graph problem, resulting in an objective function comprised of quadratic forms. The objective is then optimized via a coordinate-wise approach. The specific functional form of the objective function facilitates rigorous convergence analysis leading to convergence guarantees; an important property that cannot be established using standard results, when the dimension is larger than the sample size, as is often the case in high dimensional applications. These convergence guarantees ensure that estimators are well-defined under very general conditions, and are always computable. In addition, the approach yields estimators that have good large sample properties and also respect symmetry. Furthermore, application to simulated/real data, timing comparisons and numerical convergence is demonstrated. We also present a novel unifying framework that places all graphical pseudo-likelihood methods as special cases of a more general formulation, leading to important insights.